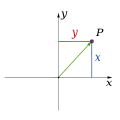İki boyutlu uzay

İki boyutlu uzay ya da kısaca 2D, içinde yaşadığımız evrenin düzlemsel yansımasının geometrik modelidir. 2 boyutlu olan (ya da görünen) varlıklar sadece genişlik ve yükseklikten oluşan düzlemsel bir yüzeye sahiptirler ve derinlikleri yoktur.
Tanımlar
"n" sayılar dizisi "n" boyutlu uzayda bir konum olarak tanımlanır."n=2" olduğunda bu tür konumlanmalar 2 boyutlu öklid uzayındadır.
İki boyutlu geometri
Politoplar
2. boyutta, sınırsız sayıda politop vardır; poligonlar. İlk yirmi aşağıda gösterilmiştir.
Dışbükey
"P" düzenli poligonu temsil eder
| İsim | Üçgen | Kare | Beşgen | Altıgen | Yedigen | Sekizgen | |
|---|---|---|---|---|---|---|---|
| Sayı | {3} | {4} | {5} | {6} | {7} | {8} | |
| Görüntü |  |
 |
 |
 |
 |
 | |
| İsim | Dokuzgen | Ongen | Onbirgen | Onikigen | Onüçgen | Ondörtgen | |
| Sayı | {9} | {10} | {11} | {12} | {13} | {14} | |
| Görüntü |  |
 |
 |
 |
 |
 | |
| İsim | Onbeşgen | Onaltıgen | Onyedigen | Onsekizgen | Ondokuzgen | Yirmigen | ...n-gen |
| Sayı | {15} | {16} | {17} | {18} | {19} | {20} | {n} |
| Görüntü |  |
 |
 |
 |
 |
 |
Küre
Düzenli tek köşeli çember ve düzenli 2 köşeli çember bozulmuş düzenli poligonlar olarak düşünülebilir. Bir küre ya da halka yüzeyinde gibi öklid olmayan bir uzayda bozulmamış bir şekilde bulunabilir.
| İsim | Tek köşeli çember | Çift köşeli çember |
|---|---|---|
| Sayı | {1} | {2} |
| Görüntü |  |
 |
İçbükey
2. boyutta sınırsız sayıda içbükey düzenli poligon vardır, {n/m} oranıyla ifade edilir. Yıldız Poligon olarak ifade edilir ve dışbükey düzenli poligonlarla aynı yatay düzlemi paylaşır. Genel olarak, herhangi bir n doğal sayısı için, there are n köşeli içbükey düzenli poligonal yıldızlar with {n/m} sembolüyle gösterilir tüm m'ler için m < n/2 (ispatı; {n/m}={n/(n-m)}) ve m ve n ortak asaldır.
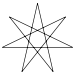
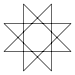
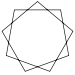
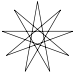
| İsim | Beş köşeli yıldız | Yedi köşeli yıldız | Sekiz köşeli yıldız | Dokuz köşeli yıldız | On köşeli yıldız | ..."n" köşeli yıldız | ||
|---|---|---|---|---|---|---|---|---|
| Sayı | {5/2} | {7/2} | {7/3} | {8/3} | {9/2} | {9/4} | {10/3} | {n/m} |
| Görüntü |  |
 |
 |
 |
 |
 |
 |
|
Tamküre
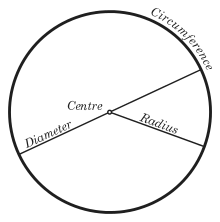
Tamküre 2 boyutlu uzayda dairedir, bu yüzden bazen daire olarak ifade edilir çünkü yüzeyi tek boyutludur. Yüzölçümü;
yarıçaptır.
İki boyutlu uzayda koordinat sistemi
Çok bilinen koordinat sistemleri Kartezyen koordinat sistemi, Polar koordinat sistemi ve Coğrafi koordinat sistemi.