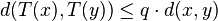Banach sabit nokta teoremi

Banach sabit nokta teoremi metrik uzaylar teorisinde kullanılan önemli bir araçtır, belli koşulları sağlayan fonksiyonların sabit noktalarının olduğunu garanti eder, ve bu sabit noktanın konstruktuf şekilde bulunmasını sağlar. Teorem Stefan Banach'ın (1892–1945) adıyla anılır, ve ilk olarak onun tarafından 1922^[1] yılında bulunmuştur.

Teorem

(X, d) boş olmayan, bir tam metrik uzay olsun. T : X → X, X üzerinde bir büzüşme olsun, yani negatif olmayan öyle bir q < 1 sayısı olsun ki tüm x, y 'ler için

$d(T(x),T(y)) \le q\cdot d(x,y)$

olsun. O zaman T 'nin X'in içinde x^* diye bir sabit noktası (yani T(x^* ) = x^* 'i sağlayan noktası) vardır, ve bu nokta biriciktir.

Kaynakça

1. http://www.emis.de/journals/BJMA/tex_v1_n1_a1.pdf