Bir Lie cebirinin kökü

Lie teorisinin matematiksel alanı içerisinde, 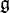$\mathfrak{g}$ bir Lie cebirinin kökü 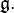$\mathfrak{g}.$ nin en büyük çözülebilir idealidir

Tanım

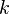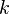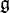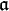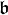Diyelimki $k$ bir alan olsun ve diyelimki $k$ üzerinde bir sonlu-boyutlu Lie cebiri olsun. Bir maksimal çözülebilir ideal, buna kök, denir,nedeni aşağıdadır. 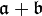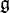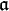İlk olarak $\mathfrak{g}$nin iki çözülebilir ideali $\mathfrak{a}$ ve $\mathfrak{b}$ olsun.Öyleyse $\mathfrak{a}+\mathfrak{b}$ $\mathfrak{g}$ yine bir idealidir ,ve çözülebilirdir çünkü $(\mathfrak{a}+\mathfrak{b})/\mathfrak{a}\simeq\mathfrak{b}/(\mathfrak{a}\cap\mathfrak{b})$ by $\mathfrak{a}$ nin bir açılımıdır.Bunun için 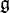$\mathfrak{g}$ olarak 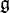$\mathfrak{g}$ nin tüm çözülebilir ideallerinin toplamı olarak tanımlayabiliriz,ayrıca bundan dolayı 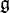$\mathfrak{g}$ nin kökü tektir. İkinci olarak 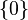$\{0\}$ ifadesi 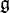$\mathfrak{g}$ bir çözülebilir idealidir,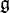$\mathfrak{g}$ nin her zaman kökü bulunmaktadır.

İlişkili konular

Bir Lie cebiri yarıbasit yalnız ve yalnız onun kökü 0dır. Bir Lie cebiri indirgemeli ancak ve ancak eşitlerin köküdür onun merkezidir.