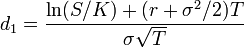Black-Scholes eşitliği

Black Scholes Eşitliği, 1973 yılında Fischer Black ve Myron Scholes tarafından yazılan "the pricing of options and corporate liabilities" adlı makalede ilk defa bahsedilen opsiyon fiyatlama tekniğidir. O zamana kadar yapılan en iyi modellemedir ve halen kullanılmaktadır.

Black Scholes Modeli, aslında rassal hareketler izleyen sıvı moleküllerini ortaya koyan Brownian Motion'ın hisse fiyatlarına ve finansal hareketlere uyarlanması sonucu ortaya çıkmıştır.

Robert C. Merton'un modelde çözülemeyen bir bölümü çözmesinden sonra, model, Black-Scholes-Merton Modeli olarak anılmaya başlamıştır.

Bu çalışmaları sayesinde, Merton ve Scholes, 1997de Ekonomi alanında Nobel Ödülü almışlardır. Black 1995 yılında vefat ettiğinden dolayı ödülü alamamıştır.

Model

Black–Scholes Modelinin önemli ayrıntıları:

• Söz konusu hissenin fiyatının hareketleri (S_t) geometrik Brownian Motion izlemektedir. Sabit bir sapma (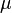$\mu$) ve volatilite ($\sigma$) olmak üzere;

$dS_t = \mu S_t\,dt + \sigma S_t\,dW_t \,$

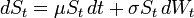
• Söz konusu hissede açığa satış (short sell) yapılması mümkündür.
• Arbitraj imkânı yoktur.
• Hisselerde el değiştirme süreklidir.
• Alımsatım maliyeti veya vergi yoktur.
• Bütün yatırım araçları tam bölünebilmelidir. (Mesela, bir aracın 1/100 nü almak mümkün olmalı.)
• Risksiz faiz ile borç alınabilmelidir.
• Hisse temettü dağıtmamalıdır. (Bu kural sadece basit BS modeli için geçerlidir.)

Yukarıdaki şartların sağlanması halinde, Avrupa satın alma opsiyonu (European call option) için, opsiyon kullanma fiyatı K ve hissenin şu andaki fiyatı S, (yani opsiyonun verdiği hak ile T zaman sonra, hisseyi K fiyatından alma imkânımız var), sabit faiz r, ve sabit volatilite $\sigma$ olmak üzere;

$C(S,T) = S\Phi(d_1) - Ke^{-rT}\Phi(d_2) \,$

Burada;

$d_1 = \frac{\ln(S/K) + (r + \sigma^2/2)T}{\sigma\sqrt{T}}$

$d_2 = \frac{\ln(S/K) + (r - \sigma^2/2)T}{\sigma\sqrt{T}} = d_1 - \sigma\sqrt{T}.$

Bu formülde 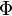$\Phi$ standart normal kümülatif dağılım işlevidir.

Bir satış opsiyonunun fiyatı alım-satım paritesi (put-call parity) ile hesaplanabilir ve aşağıdaki şekilde düzenlenebilir;

$P(S,T) = Ke^{-rT}\Phi(-d_2) - S\Phi(-d_1). \,$

Kaynak

• İngilizce wikipedia'daki BS Model maddesi