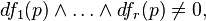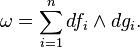Caratheodory-Jacobi-Lie teoremi

Carathéodory–Jacobi–Lie teoremi simplektik geometri içinde bir teorem olan Darboux'un teoremi'nin genellemesidir.

Açıklama

Diyelim ki M bir 2n-boyutlu simplektik manifold olsun.Simplektik formu ile ω.p ∈ M için ve r ≤ n, diyelimki f₁, f₂, ..., f_r olsun düzgün fonksiyonlar pnin bir V açık komşuluğu olarak tanımlanır.Böylece diferansiyeller her noktada doğrusal bağımlıdır,veya eşdeğeri

$df_1(p) \wedge \ldots \wedge df_r(p) \neq 0,$

burada {f_i, f_j} = 0. (Başka bir deyişle onlar involüsyon içinde çifterlidir.) Burada {–,–} Poisson braketidir-ki ise bu fonksiyonlar f_r+1, ..., f_n, g₁, g, ..., g_n pnin U  ⊂  V açık yakın komşuluğunda böylece (f_i,g_i) Mnin bir simpletik kartı, yani,ωifadesi U üzerinde olarak

$\omega = \sum_{i=1}^n df_i \wedge dg_i.$

Uygulamalar

Bir direkt uygulama olarak aşağıdakini verebiliriz. Verilen bir Hamiltonyen sistem olarak 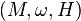$(M,\omega,H)$ burada M bir simplektik manifold ile simplektik form 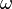$\omega$ ve H Hamiltonyen fonksiyondur, burda her nokta çevresinde 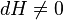$dH \neq 0$ burada bir simplektik karttır böylece onun koordinatlarının biri Htır.

Kaynakça

• Lee, John M., Introduction to Smooth Manifolds, Springer-Verlag, New York (2003) ISBN 0-387-95495-3. Graduate-level textbook on smooth manifolds.

Şablon:Differential-geometry-stub