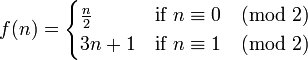Collatz sanısı

Collatz sanısı, 1'den büyük tüm doğal sayıların 1'e indirebildiğini anlatan bir teorem. Ancak daha kesinleşememiştir. Çünkü; 20 × 2⁵⁸ ≈ 5.764×10¹⁸.^[1] sayısına kadar olan sayılar, ancak kanıtlanabildi. Bu sayı ve daha yüksekleri ise daha hala matematikçiler tarafından uğraşılmaktadır.

Problemin tanımı

Collatz sanısının kuralları şudur;

• İfade olarak sayıya "x" diyelim
• Bu sayı eğer çift ise "x/2" dir.
• Bu sayı eğer tek ise "3x+1" dir.

Bu sanıya göre tüm sayılar, 1'e kolayca indirilebilir.Bu sayının büyüklüğüyle alakalı değildir.

Örneğin;

• "x=4" diyelim.O halde; 4-2-1 olur.
• "x=7" diyelim.O halde; 7-22-11-34-17-52-26-13-40-20-10-5-16-8-4-2-1 olur. Bu sayı kuramında 7'nin vardığı en büyük sayı 52'dir.

Fonksiyon olarak ifade etmek gerekirse:

$f(n) = \begin{cases} \frac{n}{2} &\mbox{if } n \equiv 0 \pmod{2}\\ 3n+1 & \mbox{if } n\equiv 1 \pmod{2} \end{cases}$

Kaynakça

1. http://www.ieeta.pt/~tos/3x+1.html