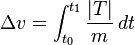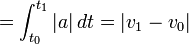Delta-v

Astrodinamik'te delta-v kavramı tam anlamıyla "hızdaki değişiklik" demek olmasına rağmen belirli bir anlamı vardır: sayıl olup sürat birimlerini alarak bir yörünge manevrası yapabilmek, başka bir ifadeyle bir rotadan başka bir rotaya geçmek için gerekecek olan "gayreti" hesaplar.

\Delta{v} = \int_{t_0}^{t_1} {\frac {|T|} {m}}\, dt

Burada

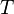T anlık itişi
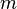m anlık kütleyi

belirler.

Dış kuvvetlerin olmaması ve itişin belli bir yönde uygulanması durumunda formül, şu basitleşmiş şekli alır:

= \int_{t_0}^{t_1} {|a|}\, dt = | {v}_1 - {v}_0 |

Bu da yalın biçimde hız değişikliğidir.

Roketler için 'dış kuvvetlerin olmaması' ile genelde atmosfer sürüklemesi ve geriye doğru aerostatik basıncın aracın burnunda olmaması ifade edilir. Bu durum vakum ispin hesaplarda kullanılmasına imkân verir ve delta-v kapasitesi böylece roket denklemiyle hesaplanır. Atmosfer kayıplarının oluşturduğu "masraflar"sa gezegen yüzeyinden kalkışlar hesaplandığında delta-v bütçesine aktarılır.

Uçuş yolları için kullanılan delta-v'ler

Bir uçuş yolu tasarlandığında delta-v, kullanılacak yakıtın ne kadar olduğunu gösteren bir göstergedir. Yakıt kullanımı, delta-v'nin roket denklemiyle gereğince hesaplanan üslü bir işlevidir.

Aracın ilk ve son konumundaki tüm enerjisini kullanarak enerjinin korunumu prensibiyle delta-v ihtiyaçlarını tespit etmek mümkün değildir. Çünkü yakıt yandığında sistemden enerji götürmektedir (aşağı da bakınız). Aynı zamanda yakılan yakıt da yok olmaktadır. Meselâ çoğu uzay aracı bir yörüngeye gönderildiğinde uzaya fırlatıldığı yerin enlemine yakın bir eğiklikle hareket ettirilir. Böylece Dünya'nın dönüşünden kaynaklanan yüzeysel hızından yararlanılmış olur. Gerekirse uzay uçuşu görevinden kaynaklanan sebeplerden dolayı uzay aracını bu eğiklikten farklı bir eğiklikle uzaya fırlatılması durumunda ilk ve son yörüngelerdeki potansiyel enerji aynı olmasına rağmen hatırı sayılır ve daha büyük bir delta-v'ye ihtiyaç vardır.

Bir rokete itiş kısa ateş darbeleriyle etkidiğinde diğer ivmeyle ilgili kaynaklar ihmâl edilebilir olabilir ve hız değişikliğinin büyüklüğü delta-v'ye bakarak basit bir yaklaşımla saptanabilir. Bu durumda etkiyecek tüm delta-v, her ayrık ateş darbesinde gereken delta-v'lerin toplamıyla basit bir şekilde hesaplanabilir. Bu, her ateş darbesinden sonra hızın büyüklüğü ve yönünün çekim etkisiyle meselâ eliptik yörüngeye girerken değişmesine rağmen böyledir.

Delta-v hesâbına örnekler görmek için Hohman transfer yörüngesi, çekimsel katapult ve gezegenlerarası sürat yoluna bakınız. Ayrıca büyük itişlerin çekimsel sürüklemeyi azalttığı da kayda değerdir.

Delta-v, aynı zamanda satelitleri gerektiği gibi yörüngede tutmak için gerekli olup itici yörüngesel konumu tutma manevralarında harcanır. Çoğu satelitlere kalkıştan önce konan yakıt sonradan tekrar yakıt tanklarına doldurulamadığından satelite başta yüklenen yakıt miktârı, pekâlâ onun ömrünü belirliyebilmektedir.

Oberth etkisi

Delta-v'nin hız yönünde uygulandığı ve güç göz önüne alındığında her delta-v birimi için kazanılan belirli yörüngesel enerjinin o anlık hıza eşit olduğu görülür. Hem o anki çekimin, hem de oluşturuduğu ivmenin değişmez olduğu bir roket ateşlemesi için her delta-v birimi için kazanılan yörüngesel enerji, ateşlemeden önce ve sonraki hızın ortalam değerine eşittir. Meselâ eliptik bir yörüngede bulunan bir yapay uydunun enerjisi yüksek hızda (yâni düşük yükseklikte) düşük hıza (yâni büyük yüksekliğe) göre daha verimli bir şekilde arttırılabilir. Bu gerçek Oberth etkisi olarak bilinir.

Ayrıca yörüngesel katapulta bakınız.

Porkchop çizimi

Gezegenlerin zamanla birbirlerine göre değişen konumlarına göre farkı delta-v'ler değişik fırlatılış târihlerine göre gerekmektedir. Bu durumu aydınlatan ve delta-v'yi zamâna karşı değişimini gösteren diyagrama kimi zaman Porkchop çizimi de denir. Bu diagram fırlatış için en uygun zaman aralığını hesaplamaya mümkün kılar. Çünkü uzaya fırlatılış, ancak kullanılan uzay aracının kapasitesi dâhilinde olmalıdır[1].

Delta-v oluşması

Delta-v, tipik olarak bir roket motorunun itişiyle ya da başka reaksyon motorlarıyla sağlanabilir. Delta-v'nin zaman değişimi motorlarca oluşan ivme büyüklüğü, başka bir ifâdeyle itişin tüm araç kütlesine oranıdır. Asıl ivme vektörü, kütle başına itiş kuvvetini çekim vektörü ve cisme etkiyen bütün diğer kuvvetlere ekleyerek bulunur.

Gereken toplam delta-v, tasarımın başlangıç safhası için iyi bir başlama noktasıdır. Daha sonra eklenen karmaşalar, tasarımın ileri safhalarında ele alınmak üzere geciktirilir.

Roket denklemi, gereken yakıtın artan delta-v'yle dramatik olarak arttığını gösterir. Bu yüzden modern uzay aracı sevk sistemlerinde hatırı sayılır çaba, uzay aracının toplam delta-v'sini azaltma ve büyük delta-v vermeye muktedir uzay araçları tasarlama yönünde harcanmıştır.

Delta-v'yi bir itiş sistemiyle arttıramak için şu tedbirler alınmalıdır:

Bunun yanı sıra (çeken gök cismine yakınken) itiş düzeyini arttırarak delta-v bâzen arttırılabilir.

Güneş Sistem etrâfındaki Delta-v'ler

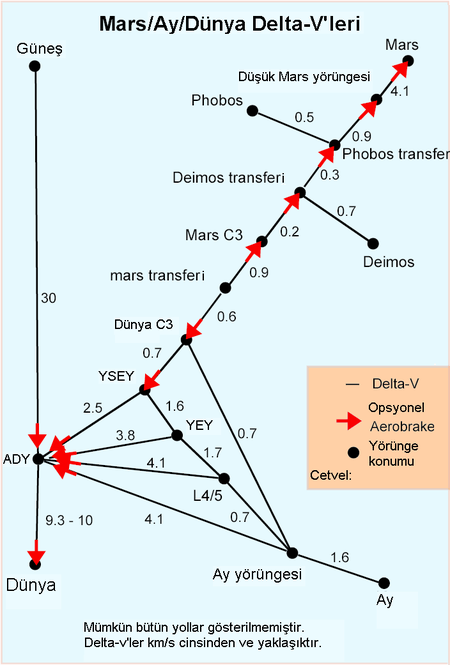
Konvensiyonel roketlerle muhtelif yörünge manevraları için km/s cinsinden delta-v'ler[2]. Kırmızı oklar, o yönde istemli hava freninin nerede kullanılabileceğini gösterirken siyah rakamlar her iki yönde uygulanan delta-v'yi km/s cinsinden göstermektedir. Gösterilenden daha düşük delta-v transferlerine çoğu zaman erişilebilirse de ender transfer zaman dilimlerinde olur veya hatırı sayılır ölçüde daha uzun sürerler. Mümkün bütün yollar gösterilmemiştir.

Kullanılan kısaltmalar

C3 Kaçış yörüngesi
YEY Yere eşzamanlı yörünge
YSEY Yere göre sâbit eşzamanlı yörünge
L5 Dünya-Ay uzaklığının beşte biri (Lagranj noktası)
ADY Alçak Dünya yörüngesi

Ayrıca bakınız

Kaynaklar

  1. ↑ Features of Mars Exploration
  2. ↑ cislunar delta-vs
This article is issued from Vikipedi - version of the 1/31/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.