Elitzur–Vaidman bomba testi

Bomba testi düzeneği. A - foton kaynağı, B - test edilecek bomba, C,D - foton dedektölerini göstermektedir. Aynaların sol alt ve sağ üst kısımları yarı varaklıdır, bir yüzeyi yarı yansıtma diğer yüzeyi ise geçirme özelliğine sahiptir.

Fizikte kuantum mekaniğinde Elitzur–Vaidman bomba testi problemi ilk olarak Avshalom Elitzur ve Lev Veidman tarafından 1993'te önerilen bir teorik deneydir.[1] Gerçek bir deney Anton Zeilinger, Paul Kwiat, Harald Weinfurter, and Thomas Herzog From the University of Innsbruck, Austria and Mark A. Kasevich of Stanford University in 1994.[2] tarafından yapılmış ve sonucu gösterilmiştir. ölçümün yapılıp yapılamadığının gösterilmesi için Mach-Zehnder interferometresi kullanılmıştır.

Problem

Bazıları sahte olan bir bomba kolleksiyonu olduğunu düşünelim. Bu bombaların şu özellikleri olduğunu varsayalım. gerçek bomblara bir foton tetiklemesiyle çalışıyorlar ve foton bombaya girdikten sonra yutuluyor ve bomba patlıyor. Sahte bombaların foton sensörleri sorunlu ve foton bomba ile etkileşime girmeden geçip gidiyor.[3]. Yani, sahte bir bomba fotonun geldiğini algılamadığı için patlamıyor. Problem şu ki, kesinlikle sahte olmayan birkaç bobma bu kolleksiyonun içinden nasıl ayıt edilebilir. Bir bomba ayıklayıcı yapılıp bunlar testten geçirilirse, foton içine girdiği anda bomba patlayacağından test etmek bütün sahte olmayan bombaların patlamasına neden olacaktır.

Çözüm

Bir çözüm gerçeklik-dışı bir gözlem yöntemi kullanan, kuantum mekaniğine dayalı bir ayıklayıcı kullanmaktır.[4]

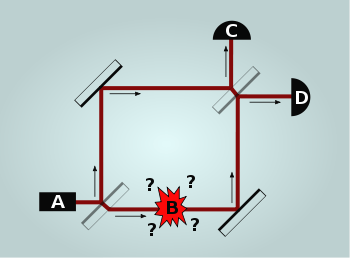
Her defasında tek bir foton gönderen bir Mach-Zehnder interferometresi ile işe başlanabilir. Bir foton yayımlandığından ve bu yarı-varaklı aynaya ulaştığında, fotonun aynadan geçme ve yansıma şansları eşittir[5]. Bir yolun üzerine fotonun çarpacağı bir bomba konulur (B). Eğer bomba sahte değilse, foton yutulur ve bomba patlar. Eğer bomba sahteyse, foton bombanın içinden etkilenmeden geçer.

Eğer fotonun durumu kuantum belirsiliğe tahvil edilirse, bir etkileşim sırasında foton aynada yansır veya içinden geçer. Bu durumda foton kuantum süperposizyon durumuna geçer, ki bu durumda tüm olasılıklar birbirleriyle etkileşim halindedir. Süperpozisyon durumu bir 'gözlemci' (dedektör) ile etkileşim içine girilinceye kadar devam eder. Gözlemci dalga fonksiyonunu çökertir ve foton kuantum belirsizlik durumundan çıkar.

Adım Adım Açıklama

Eğer bomba sahteyse:

Eğer bomba gerçekse

Sonuç olarak C dedektöründe foton algılanırsa, B dedektörünün fonksiyoneldir (bombanın gerçektir).

Bu işlemle, çalışan bombaların %25'i patlatılmadan ayıklanabilir, geri kalan %50'si patlayacak, %25'i de belirsiz olarak kalacaktır. Geri kalan 'belirsiz' bombalara da bu süreç uygulanılmaya devam edilirse başlangıçtaki sağlam bombaların %33'ü patlatılmadan ayıklanabilir. Deneyler kısmında deney değiştirilerek gerçek bombaların %100'e yakınının tespit edileceği açıklanmıştır.

Çoklu Dünyalar Yaklaşımı

Bu fenomeni açıklamanın bir yöntemi Everett'in önerdiği çoklu dünyalar yorumudur. Bu yorumda kuantum fiziğine göre birkaç farklı sonuç doğurabilecek tüm olayların oluşabilecek tüm sonuçları birden gerçekleşir, karar verme anında evren bölünüp her bir bölüm farklı bir yoldan ilerleyerek hepsini oluşturur. Bu paralel evrenler bölünmeye neden olan (kuantum pozisyonunda olarak bölünmeye sebep olan) parçacık hariç birbirinden tamamen bağımsızdır ve her birinde (bölünmeye neden olan parçacık hariç) her şeyin birer kopyası bulunmaktadır.

Çoklu dünyalar yorumuna göre, Elitzur–Vaidman bomba deneyinde fotonların süperpozisyon durumu aynı fotonun farklı paralel evrenlerdeki kopyalarının birbiriyle etkileşimi fotonun farklı durumları olarak yorumlanır. Bundan dolayı, bir foton yarı geçirgen aynayla karşılaştığında, iki evren oluşur. Bir tanesinde foton aynadan geçer ve diğer evrende aynadan yansır. Bu iki evren aynada evrenleri birbirinden ayıran foton dışında tamamen birbirinden bağımsızdır. Bir evrende aynadan geçen foton hala diğer evrende aynadan yansıyan kendi kopyasıyla etkileşime girerek, deneydeki sonucun doğmasına neden olmaktadır.

Deneyler

1994 yılında, Anton Zeilinger, Paul Kwiat, Harald Weinfurter, ve Thomas Herzog eşlenik bir deney gerçekleştirerek, etkileşimsiz ölçümlerin gerçekte mümkün olduklarını göstermişlerdir.[2]

1996 yılında, Kwait et al. seri polarizasyon cihazları kullanarak ışık çıktısı verimliliğini arttırarak foton değerini bire çok yakın bir değere yaklaştıracak yeni bir metod geliştirdi. Temek fikir foton yığınını çok sayıda çükük yığına bölmek ve bunların hepsini aynadan yansıttıktan sonra bunları tekrar birleştirmek üzerine kuruludur.[6]

Bu deney felsefik açıdan şu "gekçeklikötesi" soruya cevap aradığı için önemlidir: "Bobma sensörünün içine bir foton girerse ne olur?" Cevap "bomba gerçektir, foton tespit edildiğinden bomba patlar" ya da "bomba sahtedir, foton bomba tarafından soruğurlmaadn geçip gider." Bilinen gerçeklikte gerçek bombaların hepsi patlamış olurlar. Ancak bu deneyle kuantum boyutta bu soruya tüm çalışan bombaları patlatmadan cevap verebiliyoruz. Bu deney deneysel bir düzenek yardımıyla bunun gibi sorulara "gerçeklikötesi" cevaplar verilebileceğini göstermektedir.

Kaynakça

Şablon:Citation style

Daha fazla okuma

This article is issued from Vikipedi - version of the 12/19/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.