Freshman'ın rüyası

Iki boyutta Freshman'ın rüyası bir illüstrasyon.Karenin her kenar uzunluğu X + Y. Kare alanı sarı bölgenin alanının toplamıdır(=X²), Yeşil bölgenin alanı(=Y²), ve iki beyaz bölgenin alanı(=2×X×Y).

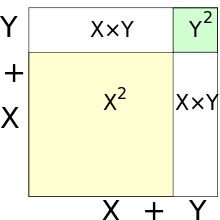
Freshman'ın rüyası bazen hataya verilen bir isimdir(x + y)ⁿ = xⁿ + yⁿ, burada n bir gerçek sayı (genellikle 1'den daha büyük bir pozitif tamsayı)dır. Başlangıç öğrencileri gerçek sayıların toplamının yaygın gücünün hesabı içinde genellikle bu hata yapar .^[1][2] n = 2 ise, bunun niçin yanlış olduğunu görmek kolaydır: (x + y)² doğru bir şekilde hesaplanabilir x² + 2xy + y² olarak dağılımlılık (veya yaygın bilinen olarak FOIL metodu) kullanılıyor. nin daha büyük pozitif tamsayı değeri için, binom teoremi yoluyla verilen sonuç doğrudur.

"Freshman'ın rüyası" adı ayrıca bazen bir asal sayı p için kaynak gösterilen teoremdir, Eğer x ve y karakteristik p nin bir değişmeli halkasının bir üyesi,ise (x + y)^p = x^p + y^p., verilen güncel "hata" nın tutarlı sonuçları, bölünebilen tüm p ilk ve son binom katsayısının koruması nedeniyle bu durum içindedir.

Örnekler

• ${\displaystyle (1+4)^{2}=5^{2}=25}$, ama ${\displaystyle 1^{2}+4^{2}=17}$.
• ${\displaystyle {\sqrt {x^{2}+y^{2}}}}$ genellikle eşit değildir ${\displaystyle {\sqrt {x^{2}}}+{\sqrt {y^{2}}}=|x|+|y|}$. Örneğin, ${\displaystyle {\sqrt {9+16}}={\sqrt {25}}=5}$, bu 3+4=7 doğru değil. Örnek içinde, hata üs ile işlenenn = ¹⁄₂ olmaktadır.

Asal karakteristik

p asal ise ve x ve y p nin karakteristik bir değişmeli halkasının üyesi ise (x + y)^p = x^p + y^p. Bu binom katsayılarının asal çarpanlarını incelenerek görülebilir: 'ninci binom katsayısı;

${\displaystyle {\binom {p}{n}}={\frac {p!}{n!(p-n)!}}.}$

sayıcıp faktöriyeldir, bu p ile bölünebilirdir. Ancak,0 < n < p ise,hiçbir n! (p − n)!de p ile bölünebilir değildir böylece tüm terimler psiz ve p asaldır. Böylece bir binom katsayısı her zaman bir tamsayıdır , ninci binom katsayısı p ile bölünebilirdir ve dolayısıyla halka içinde 0'a eşittir.Bizim sol sıfırıncı ve pinci katsayıları ile, bu ikisi 1 e eşit ise, istenen denklemi elde edilir.

Böylece p karakteristiği içinde freshman'ın rüyası bir değere eştir. Bu son gösterim p ile bir içyapı oluşturur, halka Frobenius içyapısı olarak bilinir Karakteristik p bir asal sayı olmak üzere Freshman rüyasının gerçeğine daha merkezi bir konumudur. Aslında, bir ilgili teoremi n sayısının asal olduğunu belirtmektedir ancak ve ancak (x+1)ⁿ ≡ xⁿ + 1 (mod n) polinomal rhalka ${\displaystyle \mathbb {Z} _{n}[x]}$ içindedir. Bu teorem Fermat'ın küçük Teoreminin direk bir sonucudur modern asallık testinde kilit gerçektir.^[3]

Aykırı isimler ve tarihleri

"Freshman'ın rüyası" teriminin geçmişi oldukça belirsizdir.1940 taki bir makalede modüler alanlar olarak, Saunders Mac Lane Stephen Kleene'in bölüm açıklaması karakteristik 2 nin bir alanı'nın (a + b)²= a² + b² nin cebirin yıllanmış birinci sınıf öğrencisinin bir bilgisi olacaktı. Bu belki "Freshman" ve pozitif karakteristiğin alanı içinde binom açılımı arasında ilk bağlantıdır.^[4] Böylece,cebir konuları alınan notların altyapının yazarları yaygın hatanın.İlk güncel "Freshman'ın rüyası" deyiminin onayı Hungerford's cebrin altyapısı kitaplarında (1974) görülmektedir, burada o McBrien bölümü.^[5] "Freshman üsteli" aykırı terimleri içerir, Fraleigh (1998) içinde kullanılır.^[6] "Freshman'ın rüyası" teriminin kendisi,matematik dışı konuları içinde 19. yüzyıl kayıtlarından bu yanadır.^[7]

Öyleyse (x + y)ⁿ açılımı binom teoremi ile doğrulanır,Freshman'ın rüyası ayrıca "Çocuklar'ın Binom Teoremi" ^[3] veya "erkek öğrenci Binom Teoremi" olarak da bilinir.

Ayrıca bakınız

• Asallık testi
• Sophomore'un rüyası

Kaynakça

1. Julio R. Bastida, Field Extensions and Galois Theory, Addison-Wesley Publishing Company, 1984, p.8.
2. Fraleigh, John B., A First Course in Abstract Algebra, Addison-Wesley Publishing Company, 1993, p.453, ISBN 0-201-53467-3.
3. A. Granville, It Is Easy To Determine Whether A Given Integer Is Prime, Bull. of the AMS, Volume 42, Number 1 (Sep. 2004), Pages 3–38.
4. Colin R. Fletcher, Cebir konusunda Seçilmiş makalelere bakış Susan Montgomery tarafından düzenlendi, Elizabeth W. Ralston ve diğerleri. Pp xv, 537. 1977. SBN 0 88385 203 9 (Mathematical Association of America), The Mathematical Gazette, Vol. 62, No. 421 (Oct., 1978), The Mathematical Association. p. 221.
5. Thomas W. Hungerford, Algebra, Springer, 1974, p. 121; also in Abstract Algebra: An Introduction, 2nd edition. Brooks Cole, July 12, 1996, p. 366.
6. John B. Fraleigh, A First Course In Abstract Algebra, 6th edition, Addison-Wesley, 1998. pp. 262 and 438.
7. Google books 1800–1900 search for "freshman's dream": Bentley's miscellany, Volume 26, p. 176, 1849