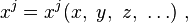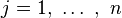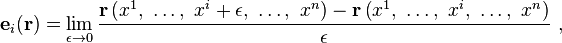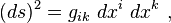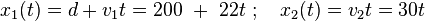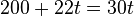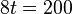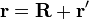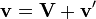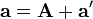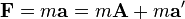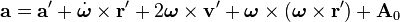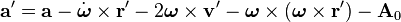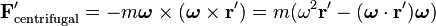Gözlemci çerçevesi

Fizikte gözlemci çerçevesi farklı zaman dilimlerinde nesnelerin konum ve yönelim gibi özelliklerini belirlemek ve ölçmek için kullanılan bir koordinat sistemini ifade etmektedir. Ayrıca bu özelliklerin temsilinde kullanılan kümelerini de içerebilmektedir. Daha zayıf bir anlamda, bir gözlemci çerçevesi yalnızca koordinatları betimlememektedir, aynı zamanda bu çerçevede hareket eden nesnelerin ayırt edilmesinde her zaman dilimi için aynı üç boyutlu alanları da tanımlamaktadır.

Einstein'ın görelilik kuramında, koordinat sistemleri hareketli bir gözlemci ve gözlem altındaki olgu ya da olaylar arasındaki ilişkiyi belirtmek için kullanılır. Bu bağlamda bu ifade "gözlemci çerçevesi" (ya da "gözlemsel sistem koordinatları") olarak belirtilir, ayrıca bu ifade mutlaka sıfır noktasında (orjinde) bulunması gerekmemesine rağmen gözlemcinin çerçeve içinde yer aldığını belirtmektedir. Bir göreli gözlemci çerçevesi koordinat zamanını da içermektedir (ya da göstermektedir), bu durum birbirine karşı hareket eden göreli çerçevelere karşı tepki göstermemektedir. Bu durum da dolayısıyla mümkün olan tüm koordine zamanlarının eşitliğini savunan Galile göreliliğinden farklıdır.

“Gözlemci çerçevesi”nin Farklı Yönleri

“Gözlemci çerçevesi”nin çeşitli anlamları arasında bir ayrıma duyulan ihtiyaç, çeşitli terimlerin ortaya çıkmasına sebebiyet vermiştir. Örneğin bazı zamanlar gözlemci çerçevesinin çeşitleri bir destekleyici olarak kullanılmaktadır, mesela Kartezyen gözlemci çerçevesi. Bazen hareket durumu, gözlemci çerçevesinin dönencesi olarak vurgulanmıştır. Bazen ise düşünülen çerçevelere yönelik dönüşüm Galile gözlemci çerçevesi olarak vurgulanmıştır. Bazen de çerçeveler kendi gözlem ölçeğine göre ayırt edilmektedir, örneğin makroskopik ve mikroskopik koordinat sistemleri gibi.

Burada, gözlemci çerçevesi terimi gözlem ya da gözlem cihazlarının koordinat seçimi ya da karakterine bağlı olmaktan çok hareketin durumuna bağlı olarak kullanılmaktadır. Bu anlamda, bir gözlemci çerçevesi bu çerçeveyle ilişkilendirilebilen koordinat sistemlerinin tüm çeşitlerindeki harekete bağlı olarak çalışılmasına fırsat vermektedir. Başka bir deyişle, bir koordinat sistemi hareket durumlarının birincil derecede endişe taşımadığı durumlarda kullanılabilmektedir. Örneğin, bir koordinat sistemi bir sistemin eşbakışımından (simetrisinden) yararlanmak için kullanılabilir. Hala geniş bir perspektif içinde, tabii ki fizikte birçok problemin denklemdirimleri; genelleştirilmiş koordinatlar, normal modlar veya özvektörleri içerebilmektedir, ve bunlar yalnızca dolaylı olarak zaman ve mekanla ilişkili olan unsurlardır. Aşağıdaki tartışmada belirtilen gözlemci çerçevelerinin çeşitli yönlerinin bırakılması önerisi oldukça yararlı görünmektedir. Bu nedenle biz gözlemci çerçevelerini, koordinat sistemlerini ve gözlemsel cihazları bağımsız kavramlar olarak aşağıdaki gibi ayırabiliriz:

• Bir gözlemsel çerçeve (durgun ya da durgun olmayan gözlemci çerçevesi gibi) hareketin durumuna ilişkin olan fiziksel bir kavramdır.

• Bir koordinat sistemi ise matematiksel bir kavram olup, gözlemleri açıklamak için kullanılan dilin seçimi ile ilgilidir. Sonuç olarak, gözlemci çerçevesi içindeki bir gözlemci herhangi bir koordinat sisteminin seçimini yönetebilir (Kartezyen, polar, kavisli, genelleştirilmiş, …) ve bunu da o gözlemci çerçevesine yapılan gözlemleri yorumlamak için kullanabilir. Bu koordinat sisteminin seçimine yönelik gerçekleşen değişim bir gözlemcinin hareket durumunu değiştirmemektedir, ve böylece gözlemcinin gözlemsel gözlemci çerçevesinde bir değişiklik gerektirmemektedir. Bu bakış açısı başka yerlerde de karşımıza çıkabilir. Bazı koordinat sistemlerinin diğer gözlem yöntemlerine göre daha iyi bir araç olduğu genellikle tartışılmamaktadır.

• Neyin gözlemleneceği ve bu gözlem için hangi gözlemsel ekipmanın seçileceği koordinat sisteminin seçimi ile gözlemcinin hareket durumundan bağımsızdır.

Aşağıda gözlemsel çerçeve hareketlerinin ℜ ve çeşitli Öklid üç-boyutlu koordinat sistemlerinin kabul edilebilirliğine ilişkin alıntılar gösterilmektedir [R, R′, vs.]:

"“Biz ilk olarak gözlemci çerçevesinin ne olduğunu tanımlarız, çerçevenin kendisi gözlemci fikri ile ilgilidir: gözlemci çerçevesi bazı anlamlarda, " Gözlemci tarafından taşınan Öklid uzayı " olarak tanımlanmaktadır. Gelin bu tanımı daha matematiksel bir şekilde detaylandıralım: gözlemci çerçevesi... gözlemcinin katı cisim hareketlerinin Öklid uzayındaki hareket kümeleridir. ℜ ile gösterilen çerçevenin gözlemci ile birlikte hareket ettiği varsayılmaktadır.… Parçacıkların uzamsal pozisyonları orjin noktası O olan bir R koordinat sistemi ile ℜ çerçevesine göreli olarak etiketlenmektedir. Eksenlerin karşılık gelen ve ℜ çerçevesinin katı cisim hareketlerini paylaşan kümesi, ℜ çerçevesinin fiziksel gerçekleşmesi olarak tanımlanır. Çerçevesindeki koordinatlar R ila R′ arasında her zaman dilimi için değişim gösterir, ve bunlar aynı koordinat transformasyonu içersindeki bu çerçevede fiziksel nicelikleri temsil eden içsel nesnelerdir (vektörler ve tansörler)."

Aynı zamanda ℜ ve [R, R′, vs.] kavramlarının birbirinden ayrılması için:

"Brillouin tarafından da belirtildiği gibi, koordinatların matematiksel kümeleri ile fiziksel gözlemci çerçeveleri arasında bir ayrım yapılması gerekmektedir. Bu tür bir ayrımın yok sayılması daha çok karmaşıklığa yol açabilecektir… Örneğin hız gibi bağımlı bileşenler fiziksel gözlemci çerçevesine göre ölçülmektedir, ancak seçilecek koordinat sistemine ilişkin denklemlerin belirlenmesinde özgürdür."

Ayrıca yine ℜ ve [R, R′, vs.] ayrımının yapılması:

"Bir gözlemci çerçevenin fikri koordinat sistemine göre gerçekten de farklılık göstermektedir. Çerçeveler farklı alanlarda (durma noktaları kümelerinde) veya zamanlarda (eşzamanlı olay kümeleri) tanımlandığı zaman çeşitlilik göstermektedir. Bu nedenle bir alanın, zamanın ya da eşzamanlı durma noktalarının fikri tamamen çerçeveye göre belirlenebilmektedir. Ancak orijinin kayması ya da uzay koordinatlarının mekansal dönüşümü yeni bir koordinat sisteminin oluşmasına sebebiyet verir. Dolayısıyla çerçeveler en iyi şekilde koordinat sistemleri sınıflarında sonuç vermektedir."

ve J. D. Norton tarafından :

"Özel ve genel görelilikteki geleneksel gelişmelerde bu çok farklı iki fikir arasındaki ayrımın yapılmaması alışkanlık haline gelmiştir. Bunlardan ilki, koordinat sistemi kavramının yalnızca uzaysal boyutlarda dört farklı düzlem olarak atanmasıdır. İkincisi, gözlemci çerçevesi, bu gibi sayıları atamak için kullanılan bir idealize sistem anlamına gelir … Gereksiz kısıtlamalardan kaçınmak için, bu metrik kavramları düzenlemeyi yok sayabiliriz … Bizim amaçlarımız için özel önem şudur ki her gözlemci çerçevesi her zaman dilimindeki olay için bir hareket durumuna sahiptir.…Özel görelilik bağlamında olduğumuz ve durgun hareket gözlemci çerçevelerinde kendimizi kısıtladığımız sürece, daha küçük bir önem eylemsizlik gözlemci çerçevesi ve eylemsiz koordinat sistemi arasındaki farka bağlı olacaktır. Özel görelilik ile kuralsız hareket içinde gözlemci çerçevesini bir kez düşünmeye başlarsak bu konforlu durumumuz derhal sona erecektir.… Daha yakın zamanlarda, Einstein'ın uygulamasındaki bariz belirsizlikler ile anlaşılmasıyla, gözlemci çerçevesi kavramı koordinat sisteminden ayrı bir yapı olarak yeniden ortaya çıkmıştır."

Bu tartışma Brading ve Castellani tarafından basit uzay-zaman koordinat sistemleri bağlamında ele alınmıştır. Genelleştirilmiş koordinatlar kullanılan koordinat sistemlerinin uzantısı Hamilton ve Lagrange tarafından formüle edilen nicem alan teorisi, klasik göreli mekanik ve nicem kütleçekimi temellerini ortaya koymaktadır.

Koordinat Sistemleri

“Koordinat sistemi” terimi (özellikle fizikçiler tarafından) teknik olmayan anlamda kullanılsa da,“koordinat sistemi” terimi matematikte ve bazen de fizikçilerin anlatmak istediği durumlarda kesin bir anlama sahiptir.

Matematikteki bir koordinat sistemi bir cebir ya da geometri yönünü temsil etmektedir, daha özel olarak ise bir manifold özelliğidir (örneğin fizikte, uzay veya durum alanlarının bir konfigürasyonudur). Bir n-boyut düzleminde bir r noktasının koordinasyonu temel olarak bir n sayı kümesinden oluşmaktadır:

$\mathbf{r} =[x^1,\ x^2,\ \dots\ , x^n] \ .$

Genel Banach uzayında bu numaralar (örneğin) Fourier serisi gibi işlevsel bir genişleme katsayısını ifade etmektedir. Fiziksel bir problemde, bunlar uzay koordinatları veya normal mod genlikleri olabilmektedir. Bir robot tasarımında göreli dönme açıları, doğrusal yer değiştirmeler, ya da bağlantı deformasyonu olarak ifade edilebilirler. Biz burada bu koordinat sisteminin bir Kartezyen koordinat sistemi ile ilgili olabileceğini varsaymaktayız:

$x^j = x^j (x,\ y,\ z,\ \dots)\ ,$    $j = 1, \ \dots \ , \ n\$

burada x, y, z vs.’ler noktanın n Kartezyen koordinatlarıdır. Bu işlevlere göre, koordinat yüzeyleri ilişkiler tarafından tanımlanmaktadır:

$x^j (x, y, z, \dots) = \mathrm{constant}\ ,$    $j = 1, \ \dots \ , \ n\ .$,

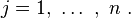Bu yüzeylerin kesişimi koordinat çizgilerini ifade etmektedir. Seçilen bir noktada, o noktadaki koordinat çizgilerinin kesişim tanjantı temel vektör dizilerini {e₁, e₂, …, e_n} olarak tanımlamaktadır. Bu da :

$\mathbf{e}_i(\mathbf{r}) =\lim_{\epsilon \rightarrow 0} \frac{\mathbf{r}\left(x^1,\ \dots,\ x^i+\epsilon,\ \dots ,\ x^n \right) - \mathbf{r}\left(x^1,\ \dots,\ x^i,\ \dots ,\ x^n \right)}{\epsilon }\ ,$

Bu değerler birim uzunlukta birimboylandırılabilir. Daha fazla ayrıntı için curvilinear koordinatları inceleyiniz.

Koordinat yüzeyleri, koordinat çizgileri ve temel vektörler koordinat sisteminin bileşenleridir. Temel vektörler her noktada dik ise, koordinat sistemi dik bir koordinat sistemi olarak ifade edilir.

Koordinat sisteminin bir diğer önemli de onun metric gergisidir. Bu da kendi koordinatı bağlamında koordinat sistemindeki yay uzunluğu olan ds’yi belirlemektedir:

$(ds)^2 = g_{ik}\ dx^i\ dx^k \ ,$

Tekrarlayan altimler toplanmaktadır.

Bu ifadelerden de anlaşılacağı gibi, bir koordinat sistemi matematiksel bir yapı olmakla birlikte aksiyomatik bir sistemin parçasıdır. Koordinat sistemleri ve fiziksel hareket arasında hiçbir zorunlu bağlantı yoktur ( veya herhangi bir ilişki boyutu bulunmamaktadır. ). Ancak koordinat sistemleri koordine olarak zamanı içerebilir, ve hareketi betimlemek için kullanılabilir. Bu nedenle, Lorentz dönüşümleri ve Galile dönüşümleri koordine dönüşümler olarak ifade edilebilir.

Gözlemsel Gözlemci Çerçevesi

Bir gözlemci çerçevesi, genellikle fiziksel bir gözlemci çerçevesi, bir gözlemci çerçevesi, ya da sadece bir çerçeve olarak tanımlanır ve gözlemci ya da gözlemcinin hareket durumuna ilişkin fiziksel bir kavramdır. Biz burada Kumar ve Barve tarafından ifade edilen görüşü benimsemekteyiz: bir gözlemci çerçevesi yalnızca onun hareket durumuna göre tanımlanmaktadır. Ancak, burada bir görüş birliği yoktur. Özel görelilikte ayrım bazen bir gözlemci ve bir çerçeve arasında yapılır. Bu bakış açısına göre bir çerçeve, zamansal vektöre dik uzayımsı vektörler kümesinin ortonormal sağ el olarak kullanımı için bir gözlemci ve bir koordinat kafesidir. Bu kısıtlı görünüm burada kullanılmamaktadır ve evrensel görelilik tartışmalarında bile kabul edilmez. Genel görelilikte koordinat sistemlerinin genel kullanımı yaygındır (bkz: örneğin, yalıtılmış bir alan dışında kütleçekimi alanı için Schwarzschild çözümünün kullanımı).

Gözlemci çerçevesinin iki türü vardır: İvmelenen ve İvmelenmeyen. Bir ivmelenmeyen gözlemci çerçevesi tüm fizik yasalarının basit biçimleriyle aldığı şekilde tanımlanmaktadır. Özel görelilikte bu çerçeveler Lorentz dönüşümleri ile ilgilidir, bunlar da hızla denklemdirilmektedir. Newton mekaniğinde, daha kısıtlı bir tanım Newton’un birinci yasasının geçerliliğini gerektirmektedir; bununla da bir Newton ivmelenmeyen gözlemci çerçevesi, serbest bir parçacığın sabit bir hızda düz bir çizgide hareket ettiğini ya da durduğunu belirtmektedir. Bu çerçeveler Galile dönüşümleri ile ilgilidir. Bu göreli ve Newton dönüşümleri Poincaré grubu ve Galile grubunun temsilleri açısından genel boyut alanlarında ifade edilmiştir.

İvmelenmeyen çerçevenin aksine bir ivmelenen gözlemci çerçevesinde, gözlemlerin açıklanabilmesi için kurgusal güçlerin çağrılması gerekmektedir. Buna yönelik bir örnek olarak, Dünya'nın yüzeyinde bir noktada merkezi olan gözlemci çerçevesi verilebilir. Bu gözlemci çerçevesi Dünya'nın merkezi etrafında yörüngelenmiştir, bu da Coriolis kuvveti, merkezcil kuvvet ve çekim kuvveti olarak bilinen kuvvetleri devreye sokmaktadır.

Ölçüm Cihazı

Bir gözlemci çerçevesinin bir başka yönü de çerçeveye eklenen ölçüm cihazının rolüdür (örneğin saatler ve çubuklar). Bu soru burada ele alınmamaktadır, ve nicem mekaniğinin özel ilgisine sahiptir, bu alanda gözlemci ve ölçüm arasındaki ilişki halen tartışılmaktadır. (Bkz. Ölçüm problemi). Fizik deneylerinde, laboratuvar ölçüm cihazlarının sahip olduğu gözlemci çerçevesi genellikle laboratuvar çerçevesi olarak ya da basitçe “lab çerçevesi” olarak adlandırılmaktadır. Buna bir örnek de bir tanecik hızlandırıcı için parçacıkların hareketsiz olduğu algıçlardaki çerçeveler olacaktır. Bazı deneylerdeki lab çerçevesi ivmelenmeyen bir çerçevedir, ancak mutlaka öyle olması gerekmemektedir. (Örneğin birçok fizik deneylerinde Dünya yüzeyindeki laboratuvar ivmelenmeyen gözlemci çerçevesi değildir.) Parçacık fiziği deneylerinde, hesaplandıkları yerde lab çerçevesinden parçacıkların enerjilerini ve momentumlarını dönüştürmek kullanışlıdır, bazen sadeleştirilen ölçümlerde momentum çerçevesinin merkezine “COM (center of momentum -frame) çerçevesi” denir, çünkü potansiyel olarak COM çerçevesi içinde mevcut olan kinetik enerji yeni parçacıklar yapmak için gerekecektir.

Bu bağlamda, saatler ve çubuklar düşüncede gözlemcinin ölçüm cihazlarını tanımlamak için kullanılmaktadır, uygulamada ise vakumun doğasına bağlı olan çok daha karmaşık ve dolaylı metrolojilerle yer değiştirir ve standart modele göre çalıştırılan, kütleçekimi zaman genişlemesinin düzenlenmesi için gerekli olan atomik saatleri kullanmaktadır. (Bkz. Ikinci, metre ve kilogram).

Aslında, Einstein saat ve çubukların yalnızca uygun ölçüm aletleri olduğunu hissetmişti ve onların atom ya da moleküller gibi daha temel varlıklarla değiştirilmesi gerektiğini düşünmüştü.

İvmelenmeyen gözlemci çerçevesi örnekleri

Basit örnek

Şekil 1: İki tane araba farlı ama sabir hızlarla hareket ediyor. Duran ivmelenmeyen gözlemci çerçevesi S yolun üzerine oturtulmuş şekildedir, hareketli ivmelenmeyen S′ gözlemci çerçevesi birinci arabaya oturtulmuştur.

Günlük yaşamda yaygın bir durum düşünün. İki araç bir yol boyunca ilerliyor, ikisi de sabit hızlarla hareket ediyor. Bkz Şekil 1. İlk anda, aralarında 200 metre mesafe bulunuyor. Öndeki araç 22 m/s hızla hareket ederken arkadaki araç ise 30 m/s hızla hareket ediyor. Eğer arkadaki aracın öndekini yakalama süresini bulmak istersek, düşünmemiz gereken üç farklı gözlemci çerçevesi bulunmaktadır. İlk olarak, araçları yol kenarından gözlemleyebiliriz. Buradaki" gözlemci çerçevesine" S diyelim. Biz burada yolun kenarında duruyoruz ve ikinci arabanın bizi geçtiği anda bir dur-saatini çalıştırıyoruz, yani bu çalıştırma işi de aralarındaki mesafe d = 200 m olduğu zaman gerçekleşmektedir. İki araba da hızlanmadığı için, onların konumlarını aşağıdaki denklemlerden hesaplayabiliyoruz, burada t süre sonunda aracın konumunu belirtmektedir ve yine t süre sonunda ikinci aracın konumunu belirtmektedir.

$x_1(t)= d + v_1 t = 200\ + \ 22t\ ; \quad x_2(t)= v_2 t = 30t$

Bu denklemlerde t=0 anında birinci araç yolun 200 m aşağısındayken ikinci aracın bizim yanıbaşımızda olduğu varsayılmaktadır. Biz durumundaki zamanı hesaplayabiliriz. Böylece $x_1=x_2$ olarak varsayımda bulunup t’yi ;

$200 + 22 t = 30t \quad$

$8t = 200 \quad$

$t = 25 \quad \mathrm{seconds}$

olarak hesaplayabiliriz.

Alternatif olarak, biz ilk arabada bulunan gözlemci çerçevesi S′ yü seçebiliriz. Bu durumda, ilk araç sabitken ikinci araç arkadan v₂ − v₁ = 8 m / s hızıyla yaklaşmaktadır. İlk aracı yakalayabilmesi için gerekli olan zaman dv₂ − v₁ = 2008 s olacaktır ve bu da 25 saniye olacaktır. Uygun gözlemci çerçevesi seçildiğinde problemin ne kadar kolay çözüldüğüne dikkat ediniz. Üçüncü uygun gözlemci çerçevesi ikinci arabaya göre gerçekleştirilebilir. Bu da az önce tartışılan çerçeveye benzerlik göstermektedir, bu durumda ise ikinci araç sabit iken ilk araç 8 m / s hızla geriye doğru gelmektedir.

Burada karmaşık bir şekilde hareket edilirken dönen ve hızlanan gözlemci çerçevesi seçilebilirdi, ancak bu seçim problemi gereksiz yere daha da zorlaştırılacaktır. Ayrıca şu da bilinmelidir ki, bir koordinat sisteminde gerçekleştirilen ölçümleri başka koordinat sistemlerine çevirmek mümkündür. Örneğin kol saatinizin yerel saate göre 5 dakika daha önde olduğunu düşünebilirsiniz. Eğer bu durumun farkında iseniz, birileri size saati sorduğunda saatinize bakıp gördüğünüz süreden 5 dakika eksik olan saati söylemeniz gerektiğini bilirsiniz. Bir sistem hakkında bir gözlemcinin yaptığı hesaplamalar gözlemcinin gözlemci çerçevesine bağlıdır (örneğin otobüs saat 3’te varıyorken siz 3’ü 5 geçe vardığını düşünebilirsiniz).

Ek Örnek

Şekil 2

İki gözlemcinin sadece yönünü içeren basit bir örnek için, bir kuzey-güney doğrultulu yolda iki insanın birbirine karşılıklı olarak durduğunu varsayalım. Bkz Resim 2. Bir araba güneye doğru onları geçmektedir. Doğuya bakan kişi için, araba sağa doğru hareket etmektedir. Ancak batıya bakan kişi için, araba sola doğru hareket etmektedir. Bu tutarsızlığın sebebi bu iki kişinin de sistemi araştırırken farklı gözlemci çerçevesi kullanmasından kaynaklanmaktadır.

Göreceli hareketteki gözlemcileri içeren daha karmaşık bir örnek için, Alfred’i düşünelim, bu varsayımda kişi kendini sağdan sola doğru geçen bir arabayı yol kenarından izlemektedir. Onun gözlemci çerçevesinde, Alfred durduğu noktayı orijin olarak, yolu x ekseni olarak ve yönü de önünde duran y ekseni olarak tanımlamaktadır. Ona göre, araba pozitif x ekseni yönünde v hızı ile x ekseni boyunca hareket etmektedir. Alfred'in gözlemci çerçevesi bir gözlemci ivmelenmeyen çerçevesi olarak tanımlanmaktadır, çünkü hızlanmamaktadır (burada Dünya’nın dönüşü ve yer çekimi ihmal edilmektedir).

Şimdi ise arabayı kullanan Betsy’i düşünelim. Betsy, gözlemci çerçevesini seçerken, durduğu noktayı orijin olarak tanımlamaktadır, sağ tarafındaki yönü pozitif x ekseni olarak, ve önündeki yönü ise pozitif y ekseni olarak tanımlamaktadır. Bu gözlemci çerçevesinde, durağan olan Betsy’dir ve onun etrafındaki Dünya da dönmektedir – örnek olarak o Alfred’i geçmiştir ve onu v hızıyla negatif y ekseni boyunca ilerliyor görmektedir. Eğer kuzeye doğru sürüyorsa, kuzey taraf pozitif y ekseni yönüdür; eğer doğuya sürüyorsa doğu, pozitif y ekseni olacaktır.

Son olarak, ivmelenen gözlemcilere ek olarak, Candace’in arabasını hızlandırdığını düşünelim. Onu geçtiği zaman, Alfred onun ivmesini hesaplamak isterse negatif x yönünde a ivmesiyle gittiğini gözlemleyecektir. Candace’in ivmesi sabit olarak varsayılırsa, Betsy’nin hesaplayacağı ivme ne olur? Eğer Betsy’nin hızı v sabit ise onun gözlemci çerçevesi ivmelenmeyen olacaktır, ve gözlemci çerçevesinde kendi ivmesini de Alfred ile aynı olarak hesaplayacaktır, negatif y yönünde a ivmesi ile. Ancak, eğer negatif y yönünde A ivmesi ile hızlanıyorsa (diğer bir deyişle, yavaşlıyorsa), Candace’in ivmesini negatif y yönünde a′ = a − A olarak hesaplayacaktır – ve bu ölçümün değeri Alfred’den biraz daha düşük olacaktır. Benzer şekilde, pozitif y-yönünde hızlanıyor ise (hızlanıyorsa), Candace’in ivmesini negatif y yönünde a′ = a + A olarak hesaplar – bu da Alfred’in değerinden biraz daha büyük olacaktır.

Gözlemci çerçeveleri özel görelilik için özellikle önemlidir, çünkü bir gözlemci çerçevesi ışık hızının önemli bir kısmıyla ilerliyorsa, o çerçevedeki zaman akışı mutlaka başka bir çerçeve içinde geçerli olmayacaktır. Işık hızı buradaki hareketli gözlemci çerçeveleri arasında tek gerçek sabit olarak kabul edilecektir.

Açıklamalar

Yukarıda yapılan çeşitli ivmelenmeyen gözlemci çerçevelerine ilişkin hesaplamaların öğrenilmesi önemlidir. Newton, örneğin, aşağıdaki örnekte olduğu gibi evrensel zamanı baz almıştır. Diyelim ki iki adet saatiniz var, ikisinin de saniye geçişleri aynı olsun. Onları aynı zamanı göstermeleri için eşzamanlı hale getirisiniz. Daha sonra iki saati birbirinden ayırarak birinin diğerine göre daha hızlı ilerlemesini sağlayalım, diğerine doğru sabit bir hızla yaklaştığını düşünelim. Newton’a göre, bu iki saat de aynı oranda saniye geçişlerine sahiptir ve ikisi de aynı zamanı gösterecektir. Newton gözlemci çerçevesi içinde ölçülen zaman oranının diğerindeki zaman oranı ile aynı olması gerektiğini söyler. Bu da evrensel zamanı gösterir ve diğer tüm gözlemci çerçevelerindeki zamanlar onların konum ve hızlarına bağlı olmadan evrensel zamanı işaret edecektir. Bu zaman kavramı ve eşzamanlılık daha sonra Einstein tarafından görelilik kuramına göre (1905) fiziksel yasalar ve anlatım ekonomisinin evrensel doğasına dayanan ivmelenmeyen gözlemci çerçeveler arasındaki dönüşümleri geliştirdiği yerde üretilmiştir (Lorentz dönüşümleri).

İvmelenmeyen gözlemci çerçevenin tanımının üç boyutlu Öklid uzayına göre uzayabileceği unutulmamalıdır. Newton burada bir Öklid uzayı varsaymıştır, ancak genel görelilik daha genel bir geometri kullanmaktadır. Bunun neden önemli olduğunu gösteren bir örnek olarak, gelin bir elips geometrisi düşünelim. Bu geometride, bir “serbest” parçacık jeodezik bir yol üzerinde sabit hızla hareket etmekte ya da durmaktadır. İki serbest parçacık da düzlemin aynı noktasından harekete başlayabilir, farklı yönlerde sabit hızlarla hareket edebilir. Belli bir süre sonra, iki parçacık elipsoitin karşı tarafında çarpışır. İki “serbest” parçacık da sabit hızla hareket eder, burada herhangi bir dış kuvvet etki etmemektedir. Herhangi bir ivme oluşmamıştır ve bu yüzden Newton'un ilk kanunu geçerliliğini korumuştur. Bu, parçacıkların ivmelenmeyen gözlemci çerçevesinde olmasıdır. Herhangi bir kuvvet etki etmediği için, bu iki parçacık birbirlerini yeniden karşılamak için bir durum geometrisi oluşturmuştur. Benzer bir şekilde, şimdi uzay-zaman olarak bilinen dört boyutlu geometrinin var olduğuna inanılmaktadır.

İvmelenen çerçeveler

Burada ivmelenen ve ivmelenmeyen gözlemci çerçeveleri düşünülmektedir. Bu çerçeveler arasındaki temel farklılık aşağıda da tarif edildiği gibi ivmelenen çerçevelerdeki gerçek olmayan kuvvetler için bir ihtiyaçtır. İvmelenen bir gözlemci çerçevesini "üşlü" çerçeve olarak tarif edebiliriz, ve bu çerçevenin bağımlı olan tüm değişkenleri üslü olarak gösterebiliriz, örn. x′, y′, a′. Bir ivmelenmeyen gözlemci çerçevesinin sıfır noktasından (orijininden) ivmelenen gözlemci çerçevesinin sıfır noktasına uzanan yöney genel olarak R ile ifade edilir. Her iki çerçevenin de ilgi noktası verilmiş iken, ivmelenmeyen sıfır noktasından bu noktaya giden yöney r, ve ivmelenen bu noktaya giden yöney ise r′ şeklinde gösterilir. Durumun geometrisinden;

$\mathbf r = \mathbf R + \mathbf r'$

Bunların ilk ve ikinci türevlerini aldığımızda ise;

$\mathbf v = \mathbf V + \mathbf v'$

$\mathbf a = \mathbf A + \mathbf a'$

Buradaki V ve A bir ivmelenmeyen sistemine göre hız ve ivmeyi ifade etmektedir ve v ile a yine ivmelenmeyen çerçeveye göre noktanın hızı ve ivmesini ifade etmektedir. Bu denklemler iki farklı koordinat sistemi arasındaki dönüşümleri sağlamaktadırlar; örneğin şimdi Newton’un birinci yasasını şu şekilde yazabiliriz:

$\mathbf F = m\mathbf a = m\mathbf A + m\mathbf a'$

Bir kuvvet etki etmeden hareketin ivmelenmesi nedeniyle bir eylemsizlik belirtisi mevcuttur. Eğer bir elektrik arabası kendi pil sistemini şarj etmeye yönelik tasarlanmış ise yavaşlama frenlemenin başlatılmasına bağlı olduğu zaman, piller yeniden şarj edilir, burada da ivmelenmenin belirtisinin fiziksel gücü ortaya çıkmaktadır. Ancak ivmelenmenin belirtisi hızlanmayı engellememektedir (ya da yavaşlamayı), ivmelenmenin belirtisi nedeniyle kuvvete bağlı hız değişimi ortaya çıkmaktadır. Dönen bir gözlemci çerçevesi perspektifinden ivmelenmenin belirtisine bakıldığında bir kuvvet uygulandığı görülür (hem merkezcil, hem de nesnenin hareketi için ortagonal yönde, Coriolis etkisi). İvmelenen gözlemci çerçevesinin yaygın bir türü de hem dönen hem de çevrilen çerçeve türüdür (buna örnek olarak bir CD’ye eklenen gözlemci çerçevesidir). Bu düzenleme, aşağıdaki denkleme yol açar (türev için Kurgusal kuvveti inceleyiniz):

$\mathbf a = \mathbf a' + \dot{\boldsymbol\omega} \times \mathbf r' + 2\boldsymbol\omega \times \mathbf v' + \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf r') + \mathbf A_0$

Ya da, ivmelenen çerçevedeki ivmeyi çözmek için;

$\mathbf a' = \mathbf a - \dot{\boldsymbol\omega} \times \mathbf r' - 2\boldsymbol\omega \times \mathbf v' - \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf r') - \mathbf A_0$

Verilen m kütlesi ile çarpıldığında ;

$\mathbf F' = \mathbf F_\mathrm{physical} + \mathbf F'_\mathrm{Euler} + \mathbf F'_\mathrm{Coriolis} + \mathbf F'_\mathrm{centripetal} - m\mathbf A_0$

burada

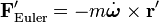$\mathbf F'_\mathrm{Euler} = -m\dot{\boldsymbol\omega} \times \mathbf r'$ (Euler force)

$\mathbf F'_\mathrm{Coriolis} = -2m\boldsymbol\omega \times \mathbf v'$ (Coriolis force)

$\mathbf F'_\mathrm{centrifugal} = -m\boldsymbol\omega \times (\boldsymbol\omega \times \mathbf r')=m(\omega^2 \mathbf r'- (\boldsymbol\omega \cdot \mathbf r')\boldsymbol\omega)$