Genetik algoritma

Genetik algoritmalar, doğada gözlemlenen evrimsel sürece benzer bir şekilde çalışan arama ve eniyileme yöntemidir. Karmaşık çok boyutlu arama uzayında en iyinin hayatta kalması ilkesine göre bütünsel en iyi çözümü arar[1].

Genetik algoritmaların temel ilkeleri ilk kez Michigan Üniversitesi'nde John Holland tarafından ortaya atılmıştır. Holland 1975 yılında yaptığı çalışmaları “Adaptation in Natural and Artificial Systems” adlı kitabında bir araya getirmiştir. İlk olarak Holland evrim yasalarını genetik algoritmalar içinde eniyileme problemleri için kullanmıştır.

Genetik algoritmalar problemlere tek bir çözüm üretmek yerine farklı çözümlerden oluşan bir çözüm kümesi üretir. Böylelikle, arama uzayında aynı anda birçok nokta değerlendirilmekte ve sonuçta bütünsel çözüme ulaşma olasılığı yükselmektedir. Çözüm kümesindeki çözümler birbirinden tamamen bağımsızdır. Her biri çok boyutlu uzay üzerinde bir vektördür.

Genetik algoritmalar problemlerin çözümü için evrimsel süreci bilgisayar ortamında taklit ederler. Diğer eniyileme yöntemlerinde olduğu gibi çözüm için tek bir yapının geliştirilmesi yerine, böyle yapılardan meydana gelen bir küme oluştururlar. Problem için olası pek çok çözümü temsil eden bu küme genetik algoritma terminolojisinde nüfus adını alır. Nüfuslar vektör, kromozom veya birey adı verilen sayı dizilerinden oluşur. Birey içindeki her bir elemana gen adı verilir. Nüfustaki bireyler evrimsel süreç içinde genetik algoritma işlemcileri tarafından belirlenirler.

Genetik Algoritmanın Genel Akış Şeması

Problemin bireyler içindeki gösterimi problemden probleme değişiklik gösterir. Genetik algoritmaların problemin çözümündeki başarısına karar vermedeki en önemli faktör, problemin çözümünü temsil eden bireylerin gösterimidir. Nüfus içindeki her bireyin problem için çözüm olup olmayacağına karar veren bir uygunluk fonksiyonu vardır. Uygunluk fonksiyonundan dönen değere göre yüksek değere sahip olan bireylere, nüfustaki diğer bireyler ile çoğalmaları için fırsat verilir. Bu bireyler çaprazlama işlemi sonunda çocuk adı verilen yeni bireyler üretirler. Çocuk kendisini meydana getiren ebeveynlerin (anne, baba) özelliklerini taşır. Yeni bireyler üretilirken düşük uygunluk değerine sahip bireyler daha az seçileceğinden bu bireyler bir süre sonra nüfus dışında bırakılırlar. Yeni nüfus, bir önceki nüfusta yer alan uygunluğu yüksek bireylerin bir araya gelip çoğalmalarıyla oluşur. Aynı zamanda bu nüfus önceki nüfusun uygunluğu yüksek bireylerinin sahip olduğu özelliklerin büyük bir kısmını içerir. Böylelikle, pek çok nesil aracılığıyla iyi özellikler nüfus içerisinde yayılırlar ve genetik işlemler aracılığıyla da diğer iyi özelliklerle birleşirler. Uygunluk değeri yüksek olan ne kadar çok birey bir araya gelip, yeni bireyler oluşturursa arama uzayı içerisinde o kadar iyi bir çalışma alanı elde edilir. Probleme ait en iyi çözümün bulunabilmesi için;

Bu durumda çözüm kümesi problem için bir noktada birleşecektir. Genetik algoritmalar, diğer eniyileme yöntemleri kullanılırken büyük zorluklarla karşılaşılan, oldukça büyük arama uzayına sahip problemlerin çözümünde başarı göstermektedir. Bir problemin bütünsel en iyi çözümünü bulmak için garanti vermezler. Ancak problemlere makul bir süre içinde, kabul edilebilir, iyi çözümler bulurlar. Genetik algoritmaların asıl amacı, hiçbir çözüm tekniği bulunmayan problemlere çözüm aramaktır. Kendilerine has çözüm teknikleri olan özel problemlerin çözümü için mutlak sonucun hızı ve kesinliği açısından genetik algoritmalar kullanılmazlar. Genetik algoritmalar ancak;

Çalışma prensibi

Genetik algoritmada kullanılan kavramlar, biyolojideki evrim teorisine benzer anlamda kullanılmaktadır. Doğal yaşamda popülasyonlar bireylerin bir arada bulunmasıyla oluşmaktadır. GA algoritması için oluşturulan popülasyon da çok sayıda bireyin bir araya gelmesiyle, başka bir deyişle çok sayıda olası çözüm adaylarının bir araya gelmesiyle oluşmaktadır. Aday çözümler, probleme uygun şekilde kodlanmış diziler halinde tutulurlar. Bu diziyi oluşturan her bir elemana birey denir ve her bir birey arama uzayında belirli bir bölgeyi temsil eder.

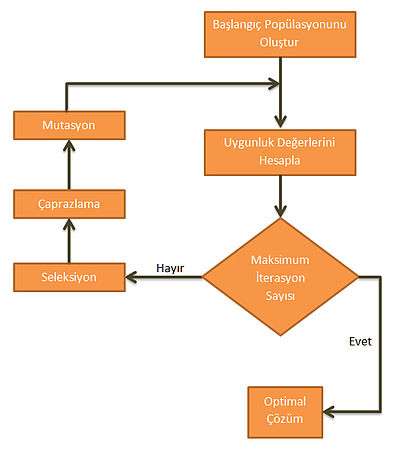
Genetik algoritmada ilk başlangıç bireyleri genellikle rastgele olarak üretilirler fakat bu bir zorunluluk değildir. Özellikle çok kısıtlı optimizasyon problemlerinde, başlangıç bireylerini oluşturmak için, tanımlanan kısıtlamaların bir kısmına dikkat edilerek daha iyi adaylar oluşturulabilinir. Bireylerin, uygunluk fonksiyonu işlemine tabi tutulması sonucunda, çözümün optimal çözüme ne kadar yaklaştığını değerlendiren uygunluk değeri belirlenir. Başlangıç popülasyonu oluşturulmuş genetik algoritma üç evrim operatörüyle çalışır. Bunlar; seçim, çaprazlama ve mutasyon operatörleridir. Genel olarak bu operatörlerin her biri, yeni nesilde oluşacak olan popülasyonun her bireyine uygulanır.

Seçim işlemi, popülasyondaki bireyleri uygunluk değerlerine bağlı olarak, yeni bireyleri oluşturmak için, ebeveyn birey seçmesi işlemidir. Çaprazlama operatörü, seçim işleminden sonra uygulanır ve ebeveyn bireylere ait kromozomların belirli kısımlarının karşılıklı yer değiştirmesini ve böylece yeni özellikte bireylerin oluşmasını ifade eder. Mutasyon işlemi ise yeni oluşan bireyin kromozomlarından herhangi birinin içindeki bir geni mutasyon olasılığına bağlı olarak değiştirme işlemidir.

Genetik algoritma işlemini sonlandırmak için çeşitli yöntemler bulunmaktadır. Bu yöntemler; algoritmanın çalışması esnasında istenen çözüm bulunduğunda, GA’nın başlangıcında tanımlanan toplam iterasyon sayısına ulaşıldığında veya uygunluk değeri sürekli olarak sabit kaldığında, bulunan en iyi bireyin temsil ettiği çözüm, problem için bulunmuş en uygun çözüm olarak sunulur.[2]

Temel Kavramlar

Genetik algoritmada; kısıtlara uyum sağlayan çözüme ulaşmak için algoritma yapısının oluşturulması ve parametrelerin belirlenmesi gerekmektedir. Aşağıda bu kavramlara ve algoritma için gerekli olan parametrelere yer verilmiştir.[2]

Gen yapısı ve kodlama

Yapısında probleme ait en küçük bilgiyi taşıyan birime gen denir. GA’nın kullandığı programlama yapısında bu gen yapıları programcının tanımlamasına bağlıdır. Bir genin yapısında sadece ikili tabandaki (binary) sayıları içerebileceği gibi, gray, tamsayı, gerçel sayı veya ağaç biçimini ve farklı sembolik ifadeleri de içerebilir. Kodlama biçimi, GA’nın performansını oldukça önemli oranda etkiler; fakat kodlama biçimi programa bağlı olduğundan bütün problemler için geçerli en uygun kodlama biçimini söylemek imkânsızdır. Michalewicz belli bir problem tipi için yapmış olduğu çalışmada gerçel sayı gösteriminin daha çabuk sonuca ulaştığını göstermiştir.

Kromozom yapısı

Bir veya birden fazla gen yapısının bir araya gelerek problemin çözümüne ait bilgilerin bir kısmını oluşturan dizilere kromozom denir. Kromozom, GA yaklaşımında üzerinde durulan en önemli birim olduğu için bilgisayar ortamında iyi ifade edilmesi gerekir.

Popülasyon

Olası çözüm bilgilerini içeren bireylerin bir araya gelmesiyle oluşan topluluğa popülasyon denir. Popülasyondaki birey sayısı problemin özelliğine göre, genetik algoritmayı tasarlayan tarafından belirlenir. Popülasyon büyüklüğü problemin çözüm süresini etkilemektedir. Popülasyondaki birey sayısının gereğinden fazla olması çözüm süresini uzatırken, birey sayısının az olması popülasyonun istenen çözüm değerine ulaşılamamasına sebep olabilir. Problemin özelliğine göre seçilecek olan popülasyondaki birey sayısı genetik algoritmayı hazırlayan kişi tarafından iyi belirlenmelidir. Grefensette, GA için en uygun popülasyon büyüklüğünün 10 ile 160 birey arasında olmasının uygun olacağını öne sürmüştür.

Genetik operatörler

GA’nın temel yapısını oluşturan ve algoritmanın işleyişi sırasında mevcut popülasyon üzerinde uygulanan işlemlere, genetik operatörler denir. Bu operatörler, seçme (selection) ya da tekrar üreme (reproduction) operatörü, çaprazlama (crossover) operatörü ve mutasyon (mutation) operatörüdür. Bunlara ilaveten kısıtlı eniyileme problemlerinde mutlak suretle kullanılması gereken ve probleme özgü olarak geliştirilen diğer bir operatör de tamir (reparation) operatörüdür. Genetik operatörler, daha iyi özelliklere sahip nesiller üreterek çözüm uzayını genişletir. Kullanılan üç standart operatör vardır:

  1. Seçim (Selection), var olan bireyi genetik yapısında herhangi bir değişiklik yapmadan yeni nesile kopyalar.
  2. Çaprazlama (Crossover), iki bireyin yapılarının rastlantısal olarak birleştirilerek yeni bireyler oluşturulmasıdır. İşlem, ikili dizilerin parçalarının değiş tokuşu ile gerçekleştirilir.
  3. Mutasyon (Mutation), var olan bir bireyin genlerinin bir ya da birkaçının yerlerinin değiştirilmesiyle oluşturulur.

Kullanım alanları

Genetik algoritmalar; Parametre ve sistem tanılama, kontrol sistemleri, robot uygulamaları, görüntü ve ses tanıma, mühendislik tasarımları, planlama, yapay zeka uygulamaları, uzman sistemler, fonksiyon ve kombinasyonel eniyileme problemleri ağ tasarım problemleri, yol bulma problemleri, çizelgeleme problemleri, sosyal ve ekonomik planlama problemleri için diğer eniyileme yöntemlerinin yanında başarılı sonuçlar vermektedir.

Diğer yöntemlerden farkı

  1. Genetik algoritmalar problemlerin çözümünü parametrelerin değerleriyle değil, kodlarıyla arar. Parametreler kodlanabildiği sürece çözüm üretilebilir. Bu sebeple genetik algoritmalar ne yaptığı konusunda bilgi içermez, nasıl yaptığını bilir.
  2. Algoritmalar aramaya tek bir noktadan değil, noktalar kümesinden başlar. Bu nedenle çoğunlukla yerel en iyi çözümde sıkışıp kalmazlar. Ancak bazı durumlarda genetik algoritmalar yerel en iyi çözüme, genel en iyi çözümden daha çabuk ulaşırlar ve algoritma bu noktada sonuçlanır. Bu durumla karşılaşıldığında, bu durumu önlemek için (genel en iyi çözüme ulaşabilmek için) ya arama uzayındaki çeşitlilik arttırılır ya da uygunluk fonksiyonu her üreme aşamasında değiştirilir.
  3. Genetik algoritmalar türev yerine uygunluk fonksiyonunun değerini kullanır. Bu değerin kullanılması ayrıca yardımcı bir bilginin kullanılmasını gerektirmez.
  4. Genetik algoritmalar gerekirci kuralları değil olasılıksal kuralları kullanır.

Kaynakça

Dış bağlantılar

  1. ↑ Elen, A. & Turan, M.K., Genetik Algoritma ile çoklu dizi hizalama probleminin çözümü, XIII. Ulusal Tıbbi Biyoloji ve Genetik Kongresi, 2013.
  2. 1 2 Elen, A., "Çizelgeleme probleminin sezgisel optimizasyon yaklaşımıyla çözümü", Yüksek Lisans Tezi, Karabük Üniversitesi Fen Bilimleri Enstitüsü, Karabük (2011).
This article is issued from Vikipedi - version of the 8/9/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.