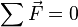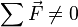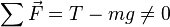Gerilim (fizik)

Gerilme, fizikte, ip, kablo, zincir veya demir çubuk, kafes kiriş gibi üç boyutlu cisimlere her iki uçtan uygulanan çekme kuvveti olarak tanımlanmaktadır. Atomik seviyede, atom veya moleküller birbirinden ayrılıp elektromanyetik potansiyel enerji kazandığında, gerilme oluşur. Gerilmiş olan çubuk veya ip eski konumlarına gelebilmek için uçlarına bağlanıp germe uygulayan objeleri ters bir kuvvetle çekecektir. Sıkıştırmanın tersi gerilmedir. Fizikte, gerilme bir kuvvet olmamasına rağmen, newton veya pound-kuvvet birimleriyle tanımlanmaktadır. İp veya tel gibi objeler, uçlarına bağlanıp gerilmelerini sağlayan objelere tersi yönde kuvvet uygularlar. Gerginlikten dolayı oluşan bu kuvvetlere germe kuvveti denilmektedir. İp veya tellerin bağlı olduğu objelerde; ivmenin sıfır olduğu dengede olan veya ivmelenmenin ve kuvvetin olduğu iki olası sistem vardır.

Tek Boyutlu Sistemlerde Gerilme

Gerilme, negatif olmayan bir sayısal büyüklüktür. Sıfır gerilme objenin gevşek durumda olduğunu belirtir. İp veya halatlar genellikle kütlesi olmayıp sadece uzunluğu olan tek boyutlu objeler olarak Kabul edilir. İp de kasnaklardan ya da titreşimlerden kaynaklı esnemeler yoksa, gerilme uçlardan uygulanan kuvvetlere eşit olacak şekilde ip boyunca sabittir. Newton'un üçüncü yasasına göre, iplere uç noktalarından uygulanan kuvvetler aynıdır. Bir ip, bir ya da daha fazla makaranın etrafında dönüyorsa, makara kütlesinin ve sürtünmenin yok sayıldığı ideal koşullarda tüm ip boyunca gerilme sabittir. Titreşen bir ip, üzerindeki gerilmeye bağlı olarak bir dizi frekansla titreşim gerçekleştirir. Bu frekanslar Newton un yasalarından elde edilir. Mikroskopik seviyede her ip parçası ip boyunca gerilmeye eşit olacak şekilde bir kuvvetle birbirlerini çekerler. İp boyunca gerçekleşen gerilme T(X) olarak gösterilir. X, ip üzerindeki herhangi bir noktadır. İp de kavislenme varsa, ip parçasına her iki komşu ip parçasından etki eden çekmeler sıfır olmaz ve yay parçası üzerinde net bir kuvvet oluşur. Net kuvvet, ivmelenmeye sebep olur. 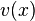Ayrıca, net kuvvet dengeleyici olup; yayın hareketi, Sturm-Louville teorisinde yer alan enine dalgaları içerir:$- \frac{d}{dx} \bigg[ \tau(x) \frac{d\rho(x)}{dx} \bigg]+v(x)\rho(x) = \omega^2\sigma(x)\rho(x)$ $v(x)$, birim uzunluktaki kuvvet sabiti. 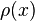$\omega^2$, yaydaki $\rho(x)$ kadar enine gerçekleştirilen yerdeğiştirme rezonanslarının özdeğeri. Yaylı çalgılardaki çeşitli harmonic hareketlerde yukarıdaki teoride açıklanabilmektedir.

Üç Boyutlu Sistemlerde Gerilme

Gerilmenin üç boyutlu uzayda gösterimi

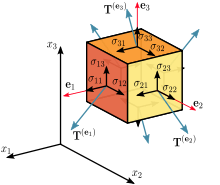
Gerilme, demir çubuk veya kafes kiriş gibi üç boyutlu malzemelerin uç noktalarına uygulanan kuvveti tanımlamak içinde kullanılmaktadır. Gerilme etkisiyle demir çubuk uzar. Yük ve uzama miktarı, tek başına kuvveten ziyade kesit alanin etki eden her kuvvete bağlı olarak malzemede deformasyonda sebep olabilir. Bu sebeple, gerilme = eksenel kuvvet / kesit alanı ifadesi mühendislik uygulamaları için daha kullanışlıdır. Gerilme, 3x3 matris boyutunda tensör olarak belirtilir. Gerilme tensörü elemanı olan $\sigma_{11}$, gerilme kuvvetinin alana oranıdır (veya sıkıştırmanın alana oranıdır. Sıkıştırmada negative sonuç vardır ancak skaler olarak aynıdır).

Denge Sistemi

Etki eden kuvvetlerin toplamı sıfır ise, sistem dengededir.

$\sum_ {} \vec{F} = 0$ ^[1]

Örneğin, yaya bağlı olan bir objenin sabit hızda düşey olarak T gerginliğinde sarkıtıldığını düşünelim. Sistem sabit bir hıza sahip ve sonuç olarak dengede çünkü yaydaki gerilme (objeyi yukarı çekme etkisi) yer çekimi kuvvetine (objeyi aşağıya çekme etkisi, mg) eşittir.

$\sum_ {} \vec{F} = \vec{T} + m\vec{g} = 0$ ^[1]

Net Kuvvet Altındaki Sistem

Dengede olmayan bir kuvvet etki ettiği zaman, sistem net bir kuvvete sahip olur. Tüm kuvvetlerin toplamı sıfır değildir. İvme ve net kuvvet her zaman bir arada bulunmaktadır.

$\sum_ {} \vec{F} \ne 0$^[1]

Örneğin, yukarda belirtilen aynı sistemi düşünelim fakat, objenin artan bir hızla aşağıya doğru sarkıtıldığını kabul edelim (artan ivmelenme). Sonuç olarak, sistemde net bir kuvvet bulunmaktadır. Bu durumda azalan ivmelenme $|mg| > |T|$ olarak belirtilir.

$\sum \vec{F} = T - mg \ne 0$^[1]

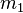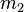Diğer örnekte, $m_1$ ve $m_2$ kütlelerine sahip birbirlerine sırasıyla sürtünmesiz bir makara üzerinden geçen iple bağlanan A ve B cisimlerini düşünelim. A cismi B cisminden daha ağır ise 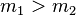$m_1 > m_2$, A cismine etki eden iki kuvvet vardır: kendisini aşağıya çeken kütlesi (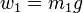$w_1=m_1g$), ve ipteki yukarı doğru çeken gerilme 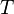$T$. Sonuç olarak, A cismi üzerindeki net kuvvet (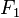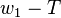$F_1$); $w_1-T$ dir. Bu sebeple, $m_1a=m_1g-T$.

Modern Fizikte İpler

Rölativistik teorideki ip benzeri objeler, mesela modern ip teorisinde kullanılan veya quarklar arasındaki etkileşim modellerinde kullanılan ipler gibi, gerilmeye sahiptirler. Enerji ip uzunluğuyla orantılıdır. Sonuç olarak, bu tip iplerde gerilme, uzama miktarından bağımsızdır. Uzayabilen iplerde, Hooke Yasası uygulanır.

Referanslar

1. Physics for Scientists and Engineers with Modern Physics, Section 5.7. Seventh Edition, Brooks/Cole Cengage Learning, 2008.

2. Jump up^ A. Fetter and J. Walecka. (1980). Theoretical Mechanics of Particles and Continua. New York: McGraw-Hill