Hamilton prensibi

Türkçeleştir

Bu maddenin içeriğinin Türkçeleştirilmesi veya Türkçe dilbilgisi ve kuralları doğrultusunda düzeltilmesi gerekmektedir. (Yabancı sözcükler yerine Türkçe karşılıklarının kullanılması, karakter hatalarının düzeltilmesi, dilbilgisi hatalarının düzeltilmesi vs.) Düzenleme yapıldıktan sonra bu şablon kaldırılmalıdır.

Fizikte, Hamilton prensibi, William Rowan Hamilton’un sabit eylem ilkesinin formülasyonudur (tarihsel formülasyonlar için bu makaleye bakın). Fiziksel bir sistemin dinamikleri Lagrange tabanli bir fonksiyonel için varyasyonel bir problemin tarafindan belirlenir. Lagrange, sistemi ve üzerine etki eden kuvvetler ile ilgili tüm fiziksel bilgileri içeren bir fonksiyondur. Varyasyonel problemi ise fiziksel sisteminde hareketin diferansiyel denklemlerine eşdeğerdir ve türetilmesini sağlar. Hamilton prensibi klasik mekaniği için formüle edilmiş olsa da elektromanyetik ve yerçekimsel alanlar gibi klasik alanlarda geçerlidir ve hatta kuantum mekaniği, kuantum alan teorisi ve kritiklik teorileri kadar uzatılmıştır.

Matematiksel formülasyonu

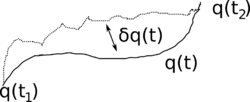
Hamilton ilkesi, bir sistemde $N$ genelleştirilmiş koordinatlarla ${\displaystyle \mathbf {q} =\left(q_{1},q_{2},\ldots ,q_{N}\right)}$ tanımlanan gerçek evrimi olan ${\displaystyle \mathbf {q} (t)}$’yi belirtilen iki durum ${\displaystyle \mathbf {q} _{1}\ {\stackrel {\mathrm {def} }{=}}\ \mathbf {q} (t_{1})}$ and ${\displaystyle \mathbf {q} _{2}\ {\stackrel {\mathrm {def} }{=}}\ \mathbf {q} (t_{2})}$ ve belirtilen iki zaman ${\displaystyle t_{1}}$ and ${\displaystyle t_{2}}$ arasında

${\displaystyle {\mathcal {S}}[\mathbf {q} ]\ {\stackrel {\mathrm {def} }{=}}\ \int _{t_{1}}^{t_{2}}L(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt}$.

eylem fonkiyonel’in durgun noktasi (varyasyonu sıfır olan nokta) olduğunu belirtiyor, ki orada ${\displaystyle L(\mathbf {q} ,{\dot {\mathbf {q} }},t)}$ sistemin Lagrange fonksiyonudur. Yani, gerçek evrimin herhangi birinci derece perturbasyonu (en fazla) ikinci derece'ye sonuçlanır, ${\displaystyle {\mathcal {S}}}$'de değişir. ${\displaystyle {\mathcal {S}}}$ eylemi bir fonksiyoneldir, yani, giriş olarak bir fonksiyonu alır ve tek bir skaler numara geri verir. In terms of functional analysis, Hamilton's principle states that the true evolution of a physical system is a solution of the functional equation

${\displaystyle {\frac {\delta {\mathcal {S}}}{\delta \mathbf {q} (t)}}=0}$

Eylem integrali için Euler-Lagrange denklemleri

Requiring that the true trajectory ${\displaystyle \mathbf {q} (t)}$ be a stationary point of the action functional ${\displaystyle {\mathcal {S}}}$ is equivalent to a set of differential equations for ${\displaystyle \mathbf {q} (t)}$ (the Euler-Lagrange equations), which may be derived as follows.

Let ${\displaystyle \mathbf {q} (t)}$ represent the true evolution of the system between two specified states ${\displaystyle \mathbf {q} _{1}\ {\stackrel {\mathrm {def} }{=}}\ \mathbf {q} (t_{1})}$ and ${\displaystyle \mathbf {q} _{2}\ {\stackrel {\mathrm {def} }{=}}\ \mathbf {q} (t_{2})}$ at two specified times ${\displaystyle t_{1}}$ and ${\displaystyle t_{2}}$, and let ${\displaystyle {\boldsymbol {\varepsilon }}(t)}$ be a small perturbation that is zero at the endpoints of the trajectory

${\displaystyle {\boldsymbol {\varepsilon }}(t_{1})={\boldsymbol {\varepsilon }}(t_{2})\ {\stackrel {\mathrm {def} }{=}}\ 0}$

To first order in the perturbation ${\displaystyle {\boldsymbol {\varepsilon }}(t)}$, the change in the action functional ${\displaystyle \delta {\mathcal {S}}}$ would be

${\displaystyle \delta {\mathcal {S}}=\int _{t_{1}}^{t_{2}}\;\left[L(\mathbf {q} +{\boldsymbol {\varepsilon }},{\dot {\mathbf {q} }}+{\dot {\boldsymbol {\varepsilon }}})-L(\mathbf {q} ,{\dot {\mathbf {q} }})\right]dt=\int _{t_{1}}^{t_{2}}\;\left({\boldsymbol {\varepsilon }}\cdot {\frac {\partial L}{\partial \mathbf {q} }}+{\dot {\boldsymbol {\varepsilon }}}\cdot {\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right)\,dt}$

where we have expanded the Lagrangian L to first order in the perturbation ${\displaystyle {\boldsymbol {\varepsilon }}(t)}$.

Applying integration by parts to the last term results in

${\displaystyle \delta {\mathcal {S}}=\left[{\boldsymbol {\varepsilon }}\cdot {\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right]_{t_{1}}^{t_{2}}+\int _{t_{1}}^{t_{2}}\;\left({\boldsymbol {\varepsilon }}\cdot {\frac {\partial L}{\partial \mathbf {q} }}-{\boldsymbol {\varepsilon }}\cdot {\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right)\,dt}$

The boundary conditions ${\displaystyle {\boldsymbol {\varepsilon }}(t_{1})={\boldsymbol {\varepsilon }}(t_{2})\ {\stackrel {\mathrm {def} }{=}}\ 0}$ causes the first term to vanish

${\displaystyle \delta {\mathcal {S}}=\int _{t_{1}}^{t_{2}}\;{\boldsymbol {\varepsilon }}\cdot \left({\frac {\partial L}{\partial \mathbf {q} }}-{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right)\,dt}$

Hamilton's principle requires that this first-order change ${\displaystyle \delta {\mathcal {S}}}$ is zero for all possible perturbations ${\displaystyle {\boldsymbol {\varepsilon }}(t)}$, i.e., the true path is a stationary point of the action functional ${\displaystyle {\mathcal {S}}}$ (either a minimum, maximum or saddle point). This requirement can be satisfied if and only if

${\displaystyle {\frac {\partial L}{\partial \mathbf {q} }}-{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}=0}$   Euler-Lagrange equations

These equations are called the Euler-Lagrange equations for the variational problem.

The conjugate momentum ${\displaystyle p_{k}}$ for a generalized coordinate ${\displaystyle q_{k}}$ is defined by the equation ${\displaystyle p_{k}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\partial L}{\partial {\dot {q}}_{k}}}}$.

An important special case of these equations occurs when L does not contain a generalized coordinate ${\displaystyle q_{k}}$ explicitly, i.e.,

if ${\displaystyle {\frac {\partial L}{\partial q_{k}}}=0}$, the conjugate momentum ${\displaystyle p_{k}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\partial L}{\partial {\dot {q}}_{k}}}}$ is constant.

In such cases, the coordinate ${\displaystyle q_{k}}$ is called a cyclic coordinate. For example, if we use polar coordinates t, r, θ to describe the planar motion of a particle, and if L does not depend on θ, the conjugate momentum is the conserved angular momentum.

Serbest parçacık kutupsal koordinatlarda

Trivial examples help to appreciate the use of the action principle via the Euler-Lagrangian equations. A free particle (mass m and velocity v) in Euclidean space moves in a straight line. Using the Euler-Lagrange equations, this can be shown in polar coordinates as follows. In the absence of a potential, the Lagrangian is simply equal to the kinetic energy

${\displaystyle L={\frac {1}{2}}mv^{2}={\frac {1}{2}}m\left({\dot {x}}^{2}+{\dot {y}}^{2}\right)}$

in orthonormal (x,y) coordinates, where the dot represents differentiation with respect to the curve parameter (usually the time, t). Therefore, upon application of the Euler-Lagrange equations,

${\displaystyle {\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)-{\frac {\partial L}{\partial x}}=0\qquad \Rightarrow \qquad m{\ddot {x}}=0}$

And likewise for y. Thus the Euler-Lagrange formulation can be used to derive Newton's laws.

In polar coordinates (r, φ) the kinetic energy and hence the Lagrangian becomes

${\displaystyle L={\frac {1}{2}}m\left({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2}\right).}$

The radial r and φ components of the Euler-Lagrangian equations become, respectively

${\displaystyle {\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {r}}}}\right)-{\frac {\partial L}{\partial r}}=0\qquad \Rightarrow \qquad {\ddot {r}}-r{\dot {\varphi }}^{2}=0}$

${\displaystyle {\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {\varphi }}}}\right)-{\frac {\partial L}{\partial \varphi }}=0\qquad \Rightarrow \qquad {\ddot {\varphi }}+{\frac {2}{r}}{\dot {r}}{\dot {\varphi }}=0.}$

The solution of these two equations is given by

${\displaystyle r={\sqrt {(at+b)^{2}+c^{2}}}}$

${\displaystyle \varphi =\arctan \left({\frac {at+b}{c}}\right)+d}$

for a set of constants a, b, c, d determined by initial conditions. Thus, indeed, the solution is a straight line given in polar coordinates: a is the velocity, c is the distance of the closest approach to the origin, and d is the angle of motion.

Maupertuis ilkesi ile karşılaştırılması

Hamilton's principle and Maupertuis' principle are occasionally confused and both have been called (incorrectly) the principle of least action. They differ in three important ways:

• their definition of the action...

Maupertuis' principle uses an integral over the generalized coordinates known as the abbreviated action ${\displaystyle {\mathcal {S}}_{0}\ {\stackrel {\mathrm {def} }{=}}\ \int \mathbf {p} \cdot d\mathbf {q} }$ where ${\displaystyle \mathbf {p} =\left(p_{1},p_{2},\ldots ,p_{N}\right)}$ are the conjugate momenta defined above. By contrast, Hamilton's principle uses ${\displaystyle {\mathcal {S}}}$, the integral of the Lagrangian over time.

• the solution that they determine...

Hamilton's principle determines the trajectory ${\displaystyle \mathbf {q} (t)}$ as a function of time, whereas Maupertuis' principle determines only the shape of the trajectory in the generalized coordinates. For example, Maupertuis' principle determines the shape of the ellipse on which a particle moves under the influence of an inverse-square central force such as gravity, but does not describe per se how the particle moves along that trajectory. (However, this time parameterization may be determined from the trajectory itself in subsequent calculations using the conservation of energy.) By contrast, Hamilton's principle directly specifies the motion along the ellipse as a function of time.

• ...and the constraints on the variation.

Maupertuis' principle requires that the two endpoint states ${\displaystyle q_{1}}$ and ${\displaystyle q_{2}}$ be given and that energy be conserved along every trajectory. By contrast, Hamilton's principle does not require the conservation of energy, but does require that the endpoint times ${\displaystyle t_{1}}$ and ${\displaystyle t_{2}}$ be specified as well as the endpoint states ${\displaystyle q_{1}}$ and ${\displaystyle q_{2}}$.

Klasik alanları için eylem prensibi

The action principle can be extended to obtain the equations of motion for fields, such as the electromagnetic field or gravity.

The Einstein equation utilizes the Einstein-Hilbert action as constrained by a variational principle.

The path of a body in a gravitational field (i.e. free fall in space time, a so called geodesic) can be found using the action principle.

Deforme olabilen cisimlere uygulanan Hamilton prensibi

Hamilton's principle is an important variational principle in elastodynamics. As opposed to a system composed of rigid bodies, deformable bodies have an infinite number of degrees of freedom and occupy continuous regions of space; consequently, the state of the system is described by using continuous functions of space and time. The extended Hamilton Principle for such bodies is given by

${\displaystyle \int _{t1}^{t2}\left[\delta W_{e}+\delta T-\delta U\right]dt=0}$

where ${\displaystyle T}$ is the kinetic energy, ${\displaystyle U}$ is the elastic energy, ${\displaystyle W_{e}}$ is the work done by external loads on the body, and ${\displaystyle t_{1},t_{2}}$ the initial and final times. If the system is conservative, the work done by external forces may be derived from a scalar potential ${\displaystyle V}$. In this case,

${\displaystyle \delta \int _{t1}^{t2}\left[T-(U+V)\right]dt=0.}$

This is called Hamilton's principle and it is invariant under coordinate transformations.

Kuantum mekaniği ve kuantum alan teorisinde Eylem prensibi

In quantum mechanics, the system does not follow a single path whose action is stationary, but the behavior of the system depends on all imaginable paths and the value of their action. The action corresponding to the various paths is used to calculate the path integral, that gives the probability amplitudes of the various outcomes.

Although equivalent in classical mechanics with Newton's laws, the action principle is better suited for generalizations and plays an important role in modern physics. Indeed, this principle is one of the great generalizations in physical science. In particular, it is fully appreciated and best understood within quantum mechanics. Richard Feynman's path integral formulation of quantum mechanics is based on a stationary-action principle, using path integrals. Maxwell's equations can be derived as conditions of stationary action.

Referanslar

• W.R. Hamilton, "On a General Method in Dynamics.", Philosophical Transaction of the Royal Society Part I (1834) p.247-308; Part II (1835) p. 95-144. (From the collection Sir William Rowan Hamilton (1805-1865): Mathematical Papers edited by David R. Wilkins, School of Mathematics, Trinity College, Dublin 2, Ireland. (2000); also reviewed as On a General Method in Dynamics)
• Goldstein H. (1980) Classical Mechanics, 2nd ed., Addison Wesley, pp. 35–69.
• Landau LD and Lifshitz EM (1976) Mechanics, 3rd. ed., Pergamon Press. ISBN 0-08-021022-8 (hardcover) and ISBN 0-08-029141-4 (softcover), pp. 2–4.
• Arnold VI. (1989) Mathematical Methods of Classical Mechanics, 2nd ed., Springer Verlag, pp. 59–61.