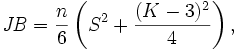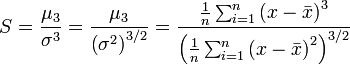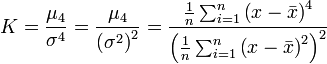Jarque-Bera sınaması

İstatistik bilim dalında, Jarque-Bera sınaması normal dağılımdan ayrılmayı ölçmek için kullanılan bir uygulama iyiliği ölçüsüdür. İlk defa bu sınamayi ortaya atan ekonemetrici A.K.Bera ve C.M.Jarque adları ile anılmaktadir.^{[1] [2]}

Yöntem

Bu sınama icin hipotezler şöyle ifade edilir:

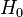$H_0$: Veriler normal dağılım gösterir

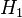$H_1$: Veriler normal dağılım göstermez.

Jarque ve Bera sınaması bir Lagranj çarpanı prensipine dayanan bir sınama tipindendir. Sınama istatistiği örneklem basıklık ve çarpıklık ölçülerinin dönüşümlerinden elde edilmiştir. Sıfır hipotezi daha ayrıntılı olarak bir bileşik hipotezdir: beklenen çarpıklığın 0 değerde ve beklenen basıklık fazlalığının 3 değerde olacağı sıfır hipotezdir; çünkü bir normal dağılım için bu değerler gereklidir.

Sınama istatistiği olan JB şöyle elde edilir:

$\mathit{JB} = \frac{n}{6} \left( S^2 + \frac{(K-3)^2}{4} \right),$

Burada n gözlem sayısı (veya genellikle serbestlik derecesi); S örneklem çarpıklık ölçüsü, K örneklem basıklık ölçüsü olur ve bu son iki istatistik şöyle tanımlanır:

$S = \frac{ \mu_3 }{ \sigma^3 } = \frac{ \mu_3 }{ \left( \sigma^2 \right)^{3/2} } = \frac{ \frac{1}{n} \sum_{i=1}^n \left( x - \bar{x} \right)^3}{ \left(\frac{1}{n} \sum_{i=1}^n \left( x - \bar{x} \right)^2 \right)^{3/2}}$

$K = \frac{ \mu_4 }{ \sigma^4 } = \frac{ \mu_4 }{ \left( \sigma^2 \right)^{2} } = \frac{\frac{1}{n} \sum_{i=1}^n \left( x - \bar{x} \right)^4}{\left( \frac{1}{n} \sum_{i=1}^n \left( x - \bar{x} \right)^2 \right)^2}$

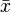Burada $\bar{x}$ örneklem ortalaması, σ² ikinci moment veya varyans ve sırasıyla μ₃ ve μ₄ üçüncü ve dördüncü merkezsel momentlerdir.

JB sınama istatistiği asimptotik olarak 2 serbestlik derecesi bulunan bir ki-kare dağılımına yaklaşır. Örneklem çarpıklığı '0'dan ve basıklığı '3'den sapma gösterdikce, JB sınama istatistiği büyüme gösterir.

Bu sınama çok kere ekonometriciler tarafından çoklu doğrusal regresyon kestirim sonuçları elde edildikten sonra ele geçen hataların normal dağılım gösterip göstermediğini araştırmak için kullanılır. ^[3] Bazı ekonometriciler bu sınama istatistiğinin bu hallerde, bağımsız değişken sayısı olan k ile düzeltilmesini önermişlerdir. ^[4]

İçsel kaynaklar

• Normallik sınamaları
• Anderson-Darling sınaması
• Kolmogorov-Smirnov sınaması
• Smirnov-Cramér-von-Mises sınaması

Referanslar

1. • Bera,Anil K. ve C.M.Jarque (1980). Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Economics Letters C.6 (3): say.255–259.
2. • Bera,Anil K. ve C.M.Jarque (1981). Efficient tests for normality, homoscedasticity and serial independence of regression residuals: Monte Carlo evidence. Economics Letters C.7 (4): say.313–318
3. Jarque,C.M. ve Bera, A. K. [1987], A test for normality of observations and regression residuals, International Statistical Review C.55, say.163–172.
4. de Verbeek(2000), Modern Econometrics, New York: Wiley say.174