Minkowski Diyagramı
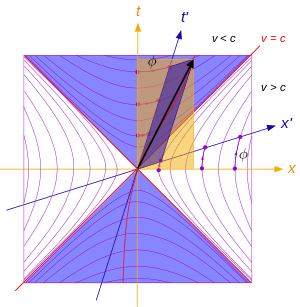
Minkowski diyagramı ya da uzay zaman diyagramı, 1908 yılında Hermann Minkowski tarafından geliştirilen ve uzay ve zaman, Özel görelilik teorisi içinde yer alan uzay ve zamanın, özelliklerinin örneklerini temin etmeyi sağlayan diyagram. Zaman genişlemesi ve uzunluk kısalması gibi fenomenlere ilişkin sayısal yönden bir kolay anlaşılabilme özelliği sağlıyordu ve bunu yaparken de matematiksel denklemleri kullanmıyordu.
Minkowski diyagramı terimi hem genel hem de bir şeye özgün olarak iki anlamda da kullanılıyordu. Genel olarak Minkowski diyagramı Minkowski uzayının bir kısmının betimlenmesi için kullanılır ve kullanılan bu uzay sıklıkla sadece tek bir boyuttan oluşana kadar kısaltılmıştır. Bunlar yani iki boyutlu diyagramlar dünya hatlarını uzaysal eksen boyunca yapılan harekete bağlı bulunan bir düzlemin kıvrımları olarak tasvir ederler. Dik olan eksen genellikle geçicidir, ve yapılan ölçümlerin birimleri negatif ya da pozitif eğim çizgileri içeren bir olaydan elde edilebilir.[1]
Bir şeye özgün olarak kullanılan Minkowski diyagramı Lorentz dönüşümlerinin sonuçlarını örneklendirme yaparak açıklar. Yatay olan eksen eş zamanlı olaylar kavramı olarak bilinen teoriye bağlı olmaktadır. Ve bu durum orijinde sabit bir şekilde bulunan gözlemci için böyle olmaktadır. Lorentz dönüşümleri iki referans koordinat sisteminin eylemsizliği ile ilişkilidir ve bu durum sadece (0,0) olayında hız değişiminin bir gözlemci tarafından yapıldığı koşullarda geçerlidir. Gözlemcinin oluşturduğu yeni zaman ekseni eski zaman ekseniyle bir açı oluşturur ve bu açı da α harfiyle gösterilir. (α < π/4)[2]
Temel öğeler

Minkowski diyagramında bulunan basitleştirmeler için genellikle sadece evrende bulunan bir boyutlu uzay içerisinde gerçekleşen olaylar ve bir zaman boyutu göz önünde bulundurulur. Yaygın olan zaman-mesafe diyagramlarından farklı olarak mesafe yatay eksen üzerinde zaman ise dikey eksen üzerinde gösterilir. Bu sebepten dolayı uzayın tek bir boyutunda gerçekleşen bu olaylar diyagram üzerinde bulunan yatay çizgiye kolay bir şekilde aktarılabilir. Diyagram üzerine çizilmiş olan objeler zaman geçtikçe aşağıdan yukarıya hareket ediyormuş gibi düşünülebilir. Bu yolla her bir obje, bir gözlemci ya da araç gibi, diyagram üzerinde kesin bir kıvrım takip eder ve buna da dünya çizgisi denir.
Diyagram üzerinde bulunan noktaların tümü zaman ve uzay içerisinde bulunan kesin noktaları temsil ederler. Örneğin diyagram üzerinde bulunan herhangi bir pozisyon, bu pozisyon içerisinde hiçbir şey gerçekleşmese bile bir olay olarak adlandırılır. Eksenler üzerindeki zaman ve uzay birimlerine yönelik yapılan ölçümler aşağıda belirtilen çiftlerden biri olarak seçilmiş olabilir:
- 30 santimetre uzunluğunda ve nanosaniyelerle ya da
- Astronomik birimler beraberinde 8 dakikalık ve 20 saniyelik aralıklar şeklinde ya da
- Işık yılları ve yıllar
Özel görelilik içinde geçen Minkowski diyagramı

1905 yılında Einstein yukarıda yazılan tanımlamanın doğru olmadığını keşfetti. 1908 yılında ise Hermann Minkowski bunun grafiksel gösterimini sağladı. Uzay ve zaman hareket eden gözlemciler olayındaki koordinatları çevirmek için kullanılan farklı kurallara öncülük eden değişik özelliklere sahiptiler. Hususi olarak bir gözlemcinin sahip olduğu bakış açısından eş zamanlı olarak gerçekleştikleri tahmin edilen olayların birbirlerinden farklı zamanlarda gerçekleştikleri düşünülüyordu.
Minkowski diyagramında eş zamanlı rölativitenin hareket eden gözlemci için ayrı bir yol ekseni tanıtımına bağlı tutulduğu biliniyordu. Yukarıda açıklanan kurala göre her bir gözlemci yol eksenlerine paralel bulunan bir çizgi üzerindeki bütün olayları eş zamalı olduklarını varsayarak yorumlamışlardır. Bir gözlemciye ait bakış açısından olayların birbiri ardından gelmesi grafiksel olarak bu çizginin diyagramın altından üstüne doğru kaydırılarak çizilebilirdi.
Tarihi
Minkowski’nin 1908 yılında kaleme aldığı kağıtta üç diyagram bulunuyordu, ilki Lorentz dönüşümlerini tasvir etmek ve ayrıca dünya çizgilerinin de çizilerek gösterilebilmesi için yapılmışlardı. Çizilen ilk diyagram bir birim hiperbolünü uygun zaman biriminin konumunu gösterebilmek için kullanıyordu (t2-x2). Bu zaman birimi hıza bağlı olarak bulunmaktaydı böylece zaman genişlemesini gösterebiliyordu. İkinci diyagram ise aynı kökten türemiş olan bir hiperbolü uzayı ayarlayabilmek için kullanıyordu. 1914 yılında Ludwik Silberstein ‘Minkowski’nin Lorentz dönüşümünü yeniden göstermesi’ adlı bir diyagram oluşturdu.[3] Bu diyagram içerisinde birim hiperbolü ve bir çift aynı kökten türemiş olan çap kullanılmıştı. 1960 yılından bugüne yapılan bu diyagramın daha çok tamamlanmış olan bir versiyonu Minkowski diyagramı olarak kullanılmaya başlandı. Ve bu tamamlanmış olan diyagram modeli özel rölativitenin dönüşüm geometrisinin standart bir simgelenimi olarak kullanıldı.
Işık hızının sabitliği
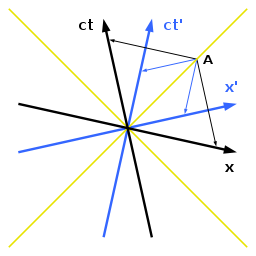
Özel görelilik kuramının doğru sayılan bir diğer özelliği de ışık hızının sabit olarak kabul edilmesidir. Bu özelliğe göre Newton’un hareket kurallarından ilkinin geçerli olduğu bir koordinat sisteminde bulunan herhangi bir gözlemci ışığın vakum hızını kendisine göre ölçerken kendi hareketi ve ışık kaynağı ne olursa olsun bu hızın her zaman aynı olduğu sonucunu elde eder. Bahsedilen durum mantığa aykırı gibi görülebilir ancak Minkowski diyagramı bu ifadenin doğru olduğuna katılmaktadır. Ayrıca yukarıda değinilen ifade Michelson-Morley deneyinin sonuçlarını da açıklamaktadır. Yapılan bu deney özel görelilik teorisi ortaya çıkmadan önce tam bir gizem olarak görülüyordu çünkü fotonların tespit edilemez bir normalin üzerindeki dalgalar olduğu düşünülmekteydi.
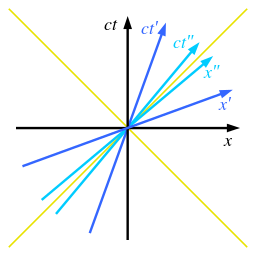
Rastgele hızlara sahip gözlemcilere bağlı olan başka koordinat sistemleri de Minkowski diyagramına dahil edilebilir. Bütün bu sistemler için her iki fotonun dünya hattı da eksenlerin açı ortaylarını ifade eder. Işık hızına ne kadar çok göreceli hız yaklaşırsa ilgili olan açı ortaya da o kadar çok eksen yaklaşır. Yolu gösteren eksen foton dünya hatlarından her zaman daha yatay iken zamanı gösteren eksen ise her zaman daha diktir. İki eksenin ölçekleri de eş değere sahipken genelde diğer koordinatlarınkinden farklıdır.
Işık hızı ve Nedensellik ilkesi
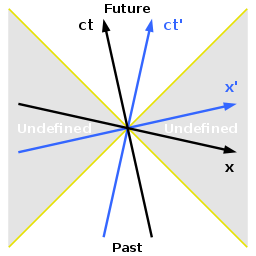
Her iki fotonun dünya hattından da daha dik olan ve orijinden geçen düz çizgiler, ışık hızından daha yavaş hareket eden objelerle uyumludur. Orijinin üstünde ve her iki fotonun dünya hattı arasında yer alan herhangi bir noktaya ışık hızından daha az bir hızla erişilebilir ve ayrıca bu nokta orijinle neden-sonuç ilişkisine de sahip olabilir. Bu alan kesin gelecektir çünkü orada yaşanan herhangi bir olay daha sonra gözlemciye aldırmadan orijin tarafından temsil edilen olayla karşılaştırılır. Bu ifadenin Minkowski diyagramında açıkça yapılmış bir grafiği bulunmaktadır.
Aynı şekilde, orijinin altında ve her iki fotonun dünya hatları arasında bulunan aralık ise orijine bağlı kesin geçmiştir. O aralıkta yaşanan herhangi bir olay kesinlikle geçmişe aittir ve bu olay orijindeki bir etkinin sonucu olabilir. Böylesine herhangi bir ikili arasındaki ilişki ‘timelike’ olarak nitelendirilir çünkü bütün gözlemciler için sıfırdan daha büyük bir zaman aralığına sahiptirler. Bu iki olayı birbirine bağlayan düz çizgi her zaman gözlemcinin zaman eksenidir. Işık hızıyla birbirlerine bağlanmış iki olaya ‘lightlike’ denir.
Prensipte, başka uzay boyutlarını Minkowski diyagramına eklemek üç boyutlu bir sunum gerektirir. Bu durumda ise geçmiş ile gelecek arasındaki aralık konilerle gösterilebilir. Bu konilere ışık konileri denir.
Eponim
Taylor ve Wheeler 1966 yılında Spacetime Physics’i oluşturduklarında, uzay-zaman geometrileri için “Minkowski Diyagramı” terimini kullanmadılar. Bunun yerine Minkowski’nin 1908’den beri felsefeye katkı sağlayan bütün yeniliklerini belirten bir içerik sundular.[4]
Minkowski diyagramı Stigler’s law of eponymy ile karşı karşıya kalmıştır ve Minkowski yanlışlıkla eponimin fikir babası olarak görülmüştür. Alexander Macfarlane’in cebir ve diyagram içeren ilk çalışmaları Minkowski diyagramına uyumlu devam etmiştir.
Ayrıca bakınız
- Minkowski uzayı
- Penrose diyagramı
- Rapidity
Kaynakça
- ↑ Mermin (1968) Chapter 17
- ↑ See Vladimir Karapetoff
- ↑ Silberstein (1914) The Theory of Relativity, page 131
- ↑ Taylor/Wheeler (1966) page 37: "Minkowski's insight is central to the understanding of the physical world. It focuses attention on those quantities, such as interval, which are the same in all frames of reference. It brings out the relative character of quantities, such as velocity, energy, time, distance, which depend on the frame of reference."