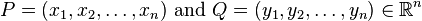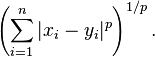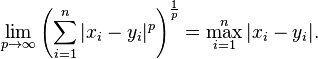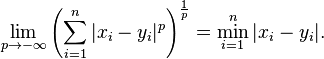Minkowski mesafesi
Minkowski mesafesi Öklid uzayı'nda bir metrik'tir iki Öklidyen mesafesi ve Manhattan mesafesi'nin bir genelleştirilmesi ile oluşturulur.
Tanım
p iki nokta arası yerine Minkowski mesafesi(uzalığı)
aşağıdaki şekilde tanımlanır:
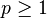 ,için Minkowski mesafesi bir metrik Minkowski eşitsizliği'nin bir sonucudur.
,için Minkowski mesafesi bir metrik Minkowski eşitsizliği'nin bir sonucudur.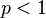 için değil,(0,0) ve (1,1) arasındaki mesafe
için değil,(0,0) ve (1,1) arasındaki mesafe 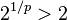 , ama nokta (0,1), bu iki nokta arasında bir mesafe 1'dir. Bu nedenle, bu üçgen eşitsizliği'ni ihlal eder.
Minkowski uzaklığı tipik kullanımı ile p olarak 1 veya 2'dir . ikincisi Öklid mesafesi'dir, önceki bazen Manhattan mesafesi olarak da bilinir.pnin sonsuza ulaşrken limitinin, eldesi Chebyshev mesafesi:
, ama nokta (0,1), bu iki nokta arasında bir mesafe 1'dir. Bu nedenle, bu üçgen eşitsizliği'ni ihlal eder.
Minkowski uzaklığı tipik kullanımı ile p olarak 1 veya 2'dir . ikincisi Öklid mesafesi'dir, önceki bazen Manhattan mesafesi olarak da bilinir.pnin sonsuza ulaşrken limitinin, eldesi Chebyshev mesafesi:
Benzer şekilde, p nin negatif sonsuza ulaşanı,için elimizde:
var. Minkowski mesafesi bir çoğul kuvvet ortalaması'ün P ve Q akıllı-bileşen arası farkı olarak da görülebilir.
p nin çeşitli değerleri ile birim çemberi gösteren görsel aşağıdadır :

Ayrıca bakınız
- Lp uzayı
Dış bağlantılar
Simple IEEE 754 implementation in C++