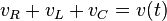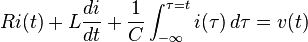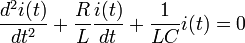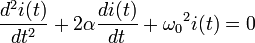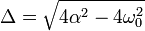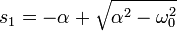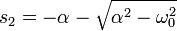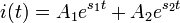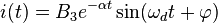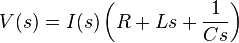RLC devresi

RLC devresi ya da LRC devresi direnç, kapasitör ve bobin'in paralel veya seri bir şekilde bağlanmasıyla oluşan bir gerilim ya da akım kaynağı tarafından beslenen bir devredir. RLC ismi direnç kapasitör ve bobinin elektriksel sembollerinin birleştirilmesi ile oluşmuştur. Bu devre de LC devresi gibi harmonik salınımlar yapar fakat devredeki dirençten dolayı eğer dış bir kaynakla beslenmezse devredeki titreşimler zamanla söner.

Bu devrelerin elektronikte birçok kullanım alanı vardır. Pasif filterler bunların en önemlisidir. Bir RLC devresinden alçak geçiren, yüksek geçiren bant geçiren ya da bant söndüren filtre olarak yapılabilir. RLC devresi ikinci derece devredir. Bu, devrenin matematiksel çözümlemesi yapıldığında ikinci derece türevsel denklemler oluşacağını belirtir. Pasif devreler tasarlarnırken bu denklemler çözülür ve denklemin istenilen katsayıları alması için devre elemanları ayarlanır.

Bir RLC devresini çözmek için kullanılan temel yaklaşım aynıdır:

• Devreye uygun Kirchoff'un voltaj ve akım yasaları yazılır.
• Bu denklemleri çözebilmek için kapasitör, bobin veya dirençin uygun ifadeleri yerleştirilir.
• İkinci derece türevsel denklem elde edebilmek için gerekli işlemler yapılır.
• Oluşan ikinci derece türevsel denklemler çözülür. İlk durumdaki şartlar da kullanılarak devrenin tam çözümü bulunur.

RLC devreleri pratikte sık sık kullanıldığından bu devrelerin özelliklerini daha kolay anlayabilmek için çeşitli kavramlar geliştirilmiştir.

Seri RLC Devresi

İlk olarak devre için Kirchhoff'un voltaj yasasını yazarsak,

Şekil 1. Seri RLC devresi

V - güç kaynağının voltajı I - devredeki akım R - direnç L - bobin C - kapasitör

$v_R+v_L+v_C=v(t) \,$

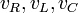Burada $v_R,v_L,v_C\,$ sırasıyla direnç, bobin ve kapasitörün voltajlarıdır.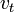$v_t\,$ ise voltaj kaynağının zamana bağlı fonksiyonudur.DC'de ise bu ifade bir sabittir.
İkinci olarak devre elemanlarının ifadelerini denklemde yerine yazarsak,

$Ri(t) + L { {di} \over {dt}} + {1 \over C} \int_{-\infty}^{\tau=t} i(\tau)\, d\tau = v(t)$

Eğer güç kaynağının voltajı değişmiyorsa denklemin türevini aldığımızda sağ taraf sıfır olur. İki tarafın da türevini alıp 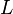$L\,$ ile bölersek,

${{d^2i(t)} \over {dt^2}}+{R \over L}{{i(t)} \over {dt}}+{1 \over {LC}}{i(t)}=0\,$

İkinci derece diferansiyel denklemimizi elde etmiş oluruz. Bu noktada fiziksel problemimiz bir ilk değer problemine dönüşmüş durumdadır. Bundan sonra denklemin homojen çözümü yapılacak ve ilk durumlar değerlendirilerek tam çözüm ortaya çıkarılacaktır. Bir seri RLC devresinden elde edeceğimiz diferansiyel denklemin genel hali şöyledir:

${{d^2i(t)} \over {dt^2}}+2\alpha{{di(t)} \over {dt}}+{\omega_0}^2 i(t)=0\,$

Bu diferansiyel denklemin diskriminantı ve kökleri,

$\Delta={\sqrt{4\alpha^2-4\omega_0^2}}\,$

$s_1= -\alpha+\sqrt{\alpha^2-\omega_0^2}\,$

$s_2= -\alpha-\sqrt{\alpha^2-\omega_0^2}\,$

ve denklemin homojen çözümü de,

$i(t)=A_{1}e^{s_1t}+A_{2}e^{s_2t}\,$

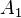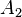olmaktadır. $A_1\,$ ve $A_2\,$ katsayıları sınır koşulları sayesinde belirlenecektir.Sınır koşulu devre hakkında bu denklemin söylediklerinden farklı olabilecek bir bilgidir. Bu devrenin ilk durumdaki voltaj-akımları ya da sonsuzdaki olası durumu olabilir.

Seri RLC Devresinin Geçici Tepkisi

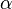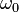Bir RLC devresinde ilk birkaç saniyede oluşan zamanla sönen tepkiye geçici tepki (ing. transient response) denir. Bu tepki yukarıda elde edilen denklemlerden yola çıkılarak bulunur. Bu diferansiyel denklemin çözümünleri diskriminantının işaretine göre üç farklı fiziksel durum ifade eder. Diskriminantın işaretini ise $\alpha\,$'nın $\omega_0\,$'ya göre büyüklüğü belirler.

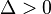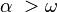• $\Delta>0\,$ yani $\alpha\ > \omega\,$ ise devre aşırı sönümlüdürhomojen çözüm tamamen reel sayılardan oluşmuştur. Devredeki voltaj salınım yapamadan söner.

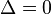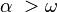• $\Delta=0\,$ yani $\alpha\ > \omega\,$ ise devre kritik sönümlüdür homojen çözüm reeldir ve iki kök birbirinin aynısıdır.

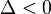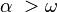• $\Delta<0\,$ yani $\alpha\ > \omega\,$ ise devre eksik sönümlüdür bu durumda denklemin kökleri birbirinin eşleniği olan iki karmaşık sayıdır. Bu durumda homojen çözüm,

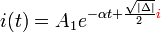$i(t)=A_1e^{-\alpha t + {\sqrt{|\Delta|} \over {2}}\color{red}i } \,$ olur.

Üstel fonksiyondaki karmaşık sayı Eulerin formülü ve bazı trigonometrik özellikler kullanılarak şu hale getirilebilir:

$i(t) = B_3 e^{-\alpha t} \sin (\omega_d t + \varphi) \,$

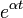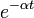bu fonksiyon $e^{\alpha t}\,$ ve $e^{-\alpha t}\,$ eğrileri tarafından çevrelenmiş bir salınıma karşılık gelmektedir.

Seri RLC Devresinin Laplace Transformu

RLC devreleri ikinci derece türevsel denklem oluşturduğundan türevsel denklemleri çözmek için kullanılan her yöntem burda kullanılabilir. Laplace transformları devrenin hem geçici tepkisini hem de AC denge durumundaki tepkisini bulabilen güçlü bir yöntemdir. İkinci derece türevsel denklemin iki tarafının türevini alırsak,

$V(s) = I(s) \left ( R + Ls + \frac{1}{Cs} \right )$

Bu denklemi I(s) için çözer ve düzenlersek,

$I(s) = \frac{s}{ L \left ( s^2 + {R \over L}s + \frac{1}{LC} \right ) } V(s)$

Bu noktadan sonra iki tarafın ters Laplasını alınmalıdır. Ters laplas alma işlemi sırasında çıkan terimler yine sınır koşulları kullanılarak yerine yazılmalıdır.