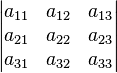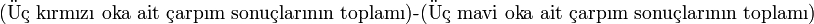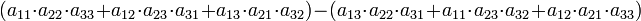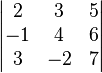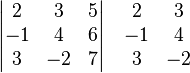Sarrus kuralı

Sarrus kuralı, "3x3" türünden matrislerin determinantını hesaplamak için pratik yoldur. Bu kural Fransız matematikçi Pierre Frédéric Sarrus tarafından keşfedilmiştir.^[1]

Hesaplanması:^[1]

$\left| \begin{matrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{matrix}\right|$

İlk iki sütundaki sayılar kopyalanarak sağ tarafına ilave edilir,^[1]

"Kırmızı ok" boyunca sayılar çarpılır ve bu üç kırmızı oka ait çarpım sonuçları toplanır."Mavi ok" boyunca sayılar çarpılır ve bu üç mavi oka ait çarpım sonuçları toplanır.^[1]

$\mbox {(Üç kırmızı oka ait çarpım sonuçlarının toplamı)-(Üç mavi oka ait çarpım sonuçlarının toplamı)}\,$

Yukarıdaki işlemlerin başka bir versiyonu: İlk iki satırdaki sayılar kopyalanarak altına ilave edilir;^[1]

"Kırmızı ok" boyunca sayılar çarpılır ve bu üç kırmızı oka ait çarpım sonuçları toplanır. "Mavi ok" boyunca sayılar çarpılır ve bu üç mavi oka ait çarpım sonuçları toplanır.^[1]

$\mbox {(Üç kırmızı oka ait çarpım sonuçlarının toplamı)-(Üç mavi oka ait çarpım sonuçlarının toplamı)}\,$

Genel formülü aşağıdaki biçimdedir:^[1]

$(a_{11} \cdot a_{22} \cdot a_{33} + a_{12} \cdot a_{23} \cdot a_{31} + a_{13} \cdot a_{21} \cdot a_{32}) - (a_{13} \cdot a_{22} \cdot a_{31} + a_{11} \cdot a_{23} \cdot a_{32} + a_{12} \cdot a_{21} \cdot a_{33})\,$

Fakat; büyük türden matrisler için bu kural geçerli değildir. Sarrus kuralı, sadece "3x3" türünden matrisler için geçerlidir.^[1]

Örnek

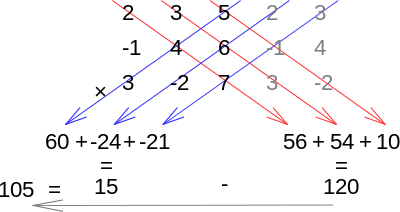
Sağ tarafa ekleme yöntemi:^[1]

$\begin{vmatrix} 2 & 3 & 5 \\ -1 & 4 & 6 \\ 3 & -2 & 7 \end{vmatrix}$

İlk iki sütunu ekleyelim:

$\begin{vmatrix} 2 & 3 & 5 \\ -1 & 4 & 6 \\ 3 & -2 & 7 \end{vmatrix}\quad \begin{matrix} 2 & 3 \\ -1 & 4 \\ 3 & -2 \end{matrix}$

Ve hesaplayalım: (2·4·7 + 3·6·3 + 5·(-1)·(-2)) – (5·4·3 + 2·6·(-2) + 3·(-1)·7) = 120 – 15 = 105

Kaynakça

1. Lehçe Vikipedi "Reguła Sarrusa" maddesi