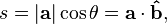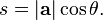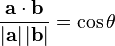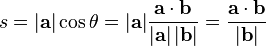Skaler izdüşüm
matematikte, bir vektörün skaler izdüşümü 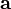 üstünde (veya üzerinde) bir vektör
üstünde (veya üzerinde) bir vektör 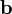 olarak, ayrıca
olarak, ayrıca 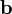 nın yönü içinde
nın yönü içinde 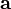 nin skalar çözünürlüğü veya skalar bileşeni olarak biliniyor , aşağıdaki ile veriliyor:
nin skalar çözünürlüğü veya skalar bileşeni olarak biliniyor , aşağıdaki ile veriliyor:
 operatör bir nokta çarpım ifade eder,
operatör bir nokta çarpım ifade eder, 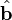 burada
burada 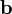 nin yönü içinde birim vektördür,
nin yönü içinde birim vektördür, 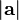 ise
ise 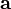 nın uzunluğudur ve
nın uzunluğudur ve 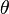
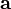 ve arası
ve arası 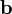 açıdır.
açıdır.
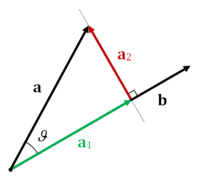
skaler izdüşüm bir skalerdir, 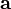 üzerinde
üzerinde 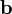 nin ortogonal izdüşümünün uzunluğuna eşittir , ile bir küçük işaret eğer izdüşüm bir karşıt yön ile sırası
nin ortogonal izdüşümünün uzunluğuna eşittir , ile bir küçük işaret eğer izdüşüm bir karşıt yön ile sırası 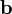 .ya var
.ya var
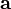 nin çarpımının skaler izdüşümü olarak
nin çarpımının skaler izdüşümü olarak 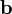
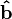 ile yukarıda sözü edilen ortogonal projeksiyonu içine onu dönüştürüyor, ayrıca adı
ile yukarıda sözü edilen ortogonal projeksiyonu içine onu dönüştürüyor, ayrıca adı 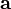 nın
nın 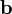 üzerinde vektör izdüşümüdür
üzerinde vektör izdüşümüdür
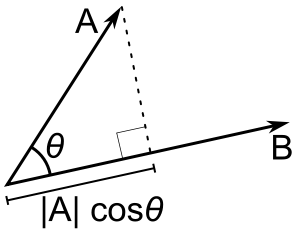
θ açısı tabanlı tanım
Eğer 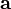 ve
ve 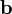 arası açı
arası açı 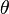 biliniyorsa
biliniyorsa 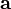 nın skaler izdüşümü olarak
nın skaler izdüşümü olarak 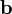 kullanılarak hesaplanabilir
kullanılarak hesaplanabilir
a ve b nin terimlerinin içindeki tanım
Eğer 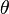 bilinmiyor
bilinmiyor 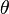 nin cosine
nin cosine 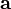 nin terimleri hesaplanabiliyor ve
nin terimleri hesaplanabiliyor ve 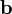 ,nokta çarpım
,nokta çarpım 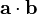 ın aşağıdaki özellikleri ile:
ın aşağıdaki özellikleri ile:
Bu özellikler ile,skaler izdüşümün tanımı  alınırsa:
alınırsa:
Özellikler
skaler izdüşümün bir negatif işaretli 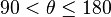 açısı varsa, O vektör izdüşümüne karşılık gelen uzunluğu ile çakışıyor ve eğer açı 90°dan küçük açı ise. Daha açığı, eğer vektör izdüşümü
açısı varsa, O vektör izdüşümüne karşılık gelen uzunluğu ile çakışıyor ve eğer açı 90°dan küçük açı ise. Daha açığı, eğer vektör izdüşümü 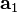 dir,ve onun uzunluğu
dir,ve onun uzunluğu 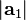 ise:
ise:
-
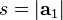 eğer
eğer 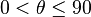 derece ise,
derece ise, -
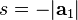 eğer
eğer 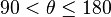 derece ise.
derece ise.
Ayrıca bakınız
- Skaler çarpım
- Çapraz çarpım
- Vektör izdüşümü