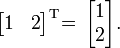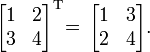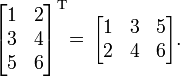Tersçapraz
Doğrusal cebirde, bir A dizeyinin tersçaprazı (transpose) AT şeklinde ifade edilir (diğer gösterimler A′, Atr or At). Bir dizeyin tersçaprazı aşağıdaki şekillerde elde edilebilir:
- A dizeyinin ilkköşegene göre yansıması alınarak AT elde edilir,
- A dizeyinin satırları AT dizeyinin sütünları olarak yazınca elde edilir,
- veya A dizeyinin sütünları AT dizeyinin satırları olarak yazılınca elde edilir.
AT dizeyinin (i,j) ögesi A dizeyinin (j,i) ile gösterilen ögesine eşittir:
Eğer A dizeyi m × n bir dizey ise AT dizeyi n × m bir dizeydir. Bir sayılın (skaler) tersçaprazı yine o sayıldır.
Örnekler
Özellikler
A, B dizeyleri ve c sayılı için aşağıdaki özellikler geçerlidir:

- Bir dizeyin tersçaprazının tersçaprazı kendisidir.

- Toplama işlemine göre yukardaki gibi dağıtılabilir.
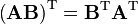
- Dizey çarpımının tersçaprazı yukardaki gibidir; dizeylerin çarpımının sırası değişir ve iki dizeyinde tersçaprazı alınır. Dizey çarpımında sıra değişikliğine dikkat edilmesi gereklidir.

- Sayıl ile dizey çarpımının tersçaprazı alınırken sayıl olduğu gibi bırakılır ve dizeyin tersçaprazı alınır. Sayılın tersçaprazı kendisine eşittir ve dizey ile sayıl çarpılırken çarpımın sırası önemli değildir.

- Kare bir dizey için dizeyin dizey değerliği (determinantı) ile o dizeyin tersçaprazının dizey değerliği aynıdır.
- İki yöneyin, a ve b, nokta çarpımı aşağıdaki gibi hesaplanabilir:
bu çarpımda ai bi şeklinde Einstein gösterimi kullanılarak yazılabilir. Burada i alt imi ve i üst iminin aynı olması i üzerinden toplama yapılacağı manasına gelmektedir.

- Tersi alınabilir bir dizeyin tersçaprazının da tersi alınabilir. Yukarıdaki A dizeyinin tersçaprazının tersi ile tersinin tersçaprazı birbirine eşittir. Herhangi bir dizeyin tersinin tersçaprazının tersi kendisine eşittir. A−T şeklinde yazım yukardaki eşitlikteki sağ veya sol taraftaki terimlerden herhangi birini ifade etmek için kullanılır.
- Eğer A kare bir dizey ise bu dizeyin özdeğerleri ile tersçaprazlarının özdeğerleri birbirine eşittir.
This article is issued from Vikipedi - version of the 3/5/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![[\mathbf{A}^\mathrm{T}]_{ij} = [\mathbf{A}]_{ji}](../I/m/676a09fb68a5cfb70409594b8622e226.png)