Treap

Treap genel gorunus.

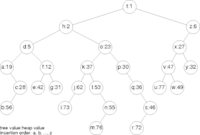
Treap ya da tree heap (ağaç öbeği), arama, ekleme, silme gibi temel işlemler için log(n) zamanı garanti eden dinamik bir ikili arama ağacıdır. İkili arama ağacına sıralı şekilde ekleme yapılırsa binary arama ağacı bağlantılı listeye dönüşür ve arama ancak O(n) zamanda yapılabilir. Bu durumu ortadan kaldırmak için treap her düğümde binary arama ağacında kullanılan asıl değere ek olarak bir de rastgele olusturulmus bir anahtar tutar. Treap veri yapısı hem asıl değere göre veri ağacının kurallarına uyularak hem de rastgele anahtar ata düğümden küçük olacak şekilde kurulur.

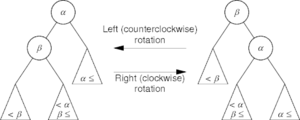
Treap ilk defa Cecilia R. Aragon ve Raimund Seidel tarafından 1989 yılında önerilmistir.[1][2] Treap adı İngilizce ağaç anlamına gelen "tree" ve öbek anlamına gelen "heap" sözcüklerinin birleştirilmesinden oluşmuştur. Treap oluşturulurken ağaç yapısını bozmayacak şekilde işlemler icra edilir ardından treap'in heap yapısını bozmamak adına gerekli düzeltmeler sağa veya sola döndurme (right or left rotate) işlemleri ile yapılır.

Treap değerlerin rastgele anahtarlara gore sıralı olarak eklenmesi şeklinde de düzeltme işlemleri yapılmadan oluşturulabilir.

Butun degerleri rastgele bir sirayla eklenmis bir agacta rastgele secilen bir elemana uzaklik O(log n)'dir. Kok dugumden secilen herhangi bir baska elemana gidilirken su an bulundugumuz elemanin altinda n elaman oldugunu varsayalim.Su an ki elamanin bizim aradigimiz elaman olma olasiligi n elaman rastgele bicimde dagildigindan 1/n'dir.Sol alt agac p-1 eleman barindirdigindan ayni mantikla gitmek istegimiz elemanin orada olma olasiligi p-1/n'dir. Ayni sekilde sag alt agac n-p dugum barindirdigindan olasilik n-p/n'dir. Bir adimda gelinecek alt agac buyuklugunun beklenen degeri (p-1)·(p-1)/n + (n-p)·(n-p)/n + (1·1/n) olarak ortaya cikar. P'nin butun degerleri 1 ile n arasinda esit olasilikla dagildigindan her adimda ziyaret edilecek agac buyuklugude ayni sekilde dagilir. Yukaridaki ifadenin 1'den n'e kadar degerlerinin n ile bolumu: (1/n)∑ (p-1)2/n + (n-p)2/n + 1 = (1/n)((2/3)n2 - n + 4/3) = (2/3)n + O(1/n) seklinde ortaya cikar.[3] Bu ifadeninde gosterdigi gibi, O(log 3/2n) adimda istenilen noktaya ulasilmasi beklenir. Bu sebepten ekleme, silme ya da arama islemlerinin O(log n) zamanda yapilabilir.

Operasyonlar/Islemler

Arama

Arama islemi ikili arama agacindaki gibi anahtar degerleri goz ardi edilerek yapilir.

Ekleme

Bir x degerini agaca eklemek icin rastgele olacak sekilde bir p anahtar degeri uretilir. Agaca ikili arama yapildiktan sonra uygun dugumde yeni bir yaprak dugum olusturulur.Bu noktadan sonra p degeri dugumun atasindan kucuk olana kadar saga ya da sola dondurme islemi dugum uzerinde uygulanir. Boylece hem agac yapisi hem de heap ozelligi korunmus olur.

Silme

Bir x degerini agactan silmek icin once ikili arama yapilarak dugumun yeri tespit edilir. Eger dugum bir yaprak dugumse silinir. Eger degilse tek cocugu varsa aralarinda dondurme islemi uygulanarak dugum yaprak dugum haline getirilir. Eger birden fazla cocuk varsa p degerine gore uygun olan cocuk secilerek dondurme islemi uygulanir. Bu islemler dugum yaprak dugum oluncaya kadar devam eder.

Treap'in Bolunmesi

Bir Treap istenilen bir noktadan iki ayri treap'e bolunmek istendiginde iki farkli durum ortaya cikar. Bolunmenin istendigi deger treapte mevcut degilse o deger en yuksek anahtar degeriyle treap'e eklenerek degerin kok dugum olmasi saglanir. Ardindan dugumun sol cocugu ve sag cocugu iki ayri treap olarak kok dugumden baglantilari koparilir. Deger Treapin icinde ise degerin bulunmasina mutakip deger uygun dondurme islemleriyle kok dugum yapilir. Kok dugumun sol ya da sag cocugunun kok ile baglantisi koparilarak ayri bir treap olarak kullanilabilir. Bu islem basitce bir ekleme islemi yapmakla ayni zamanda yani O(log n) zamanda tamamlanir.

Bolunen Treap'lerin Birlesmesi

Iki treap birlestirilirken on sart olarak bir treap'teki en buyuk degerin obur treapteki en kucuk degerden kucuk oldugu kabul edilir. Ilk treapteki en buyuk elemandan buyuk diger treapteki en kucuk elemandan kucuk olacak sekilde bir x degeri agaca en kucuk anahtar degeriyle eklenir(sol cocuk ve sag cocuk treap kok dugumleri olacak sekilde). Ekleme isleminden sonra bu dugum yaprak dugum olacagindan kolayca silinir ve elimizde birlesmis bir treap kalir. Bu islemde bolunme islemi gibi ekleme islemi kadar yani O(log n) zamanda tamamlanir.

Saga ve sola dondurme islemi
Eleman Sayisi

Ikili arama agaclarinda kullanilan lokal bir degiskeni ekleme basarili oldugunda arttirmak ve silme islemi basarili oldugunda azaltmak bolunme ve birlesme islemleri sonrasi treap icin hatali sonuc verir. Bu yaklasimin yerine her dugumde sag ve sol cocuk sayilari tutulmali ve bu sayilar dondurme islemleri sonunda guncellenmelidir. Bu yontemle hatasiz bir bicimde treapin eleman sayisi bolunme ve birlesme islemleri sonucu O(1) zamanda ogrenilebilir.

Kaynakça

  1. ↑ Aragon, Cecilia R.; Seidel, Raimund (1989), "Randomized Search Trees", Proc. 30th Symp. Foundations of Computer Science (FOCS 1989), Washington, D.C.: IEEE Computer Society Press, pp. 540–545, doi:10.1109/SFCS.1989.63531, ISBN 0-8186-1982-1
  2. ↑ Seidel, Raimund; Aragon, Cecilia R. (1996), "Randomized Search Trees", Algorithmica 16 (4/5): 464–497, doi:10.1007/s004539900061
  3. ↑ [ http://www.cs.cornell.edu/Courses/cs312/2003sp/lectures/lec26.html] treap lecture
Yararli Kaynaklar
This article is issued from Vikipedi - version of the 12/28/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.