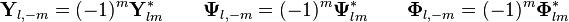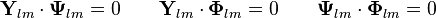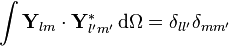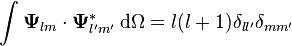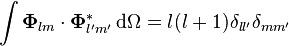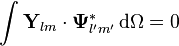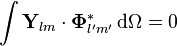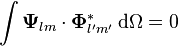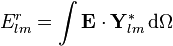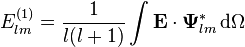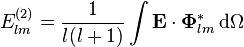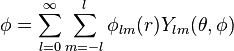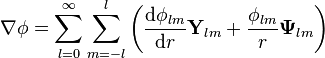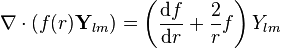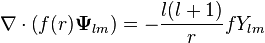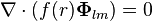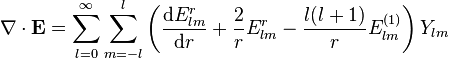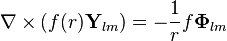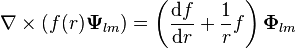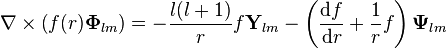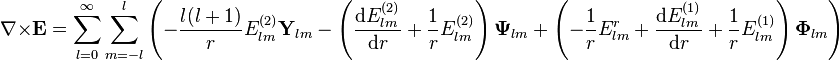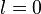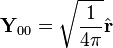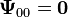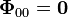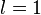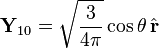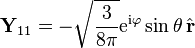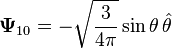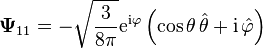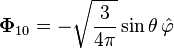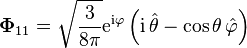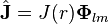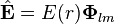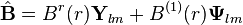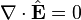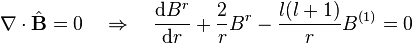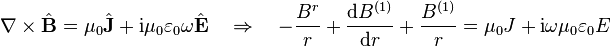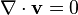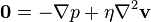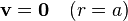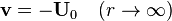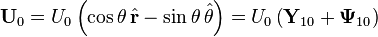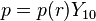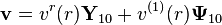Vektör küresel harmonikler

Ana özellikler

Simetri

Skaler küresel harmonikleri gibi,VSH eldesi

$\mathbf{Y}_{l,-m} = (-1)^m \mathbf{Y}^*_{lm}\qquad\mathbf{\Psi}_{l,-m} = (-1)^m \mathbf{\Psi}^*_{lm}\qquad\mathbf{\Phi}_{l,-m} = (-1)^m \mathbf{\Phi}^*_{lm}$

Diklik

VSH genellikle üç-boyutlu yol içinde diktir

$\mathbf{Y}_{lm}\cdot\mathbf{\Psi}_{lm}=0\qquad\mathbf{Y}_{lm}\cdot\mathbf{\Phi}_{lm}=0\qquad\mathbf{\Psi}_{lm}\cdot\mathbf{\Phi}_{lm}=0$

Ve Hilbert uzayı için

$\int\mathbf{Y}_{lm}\cdot \mathbf{Y}^*_{l'm'}\,\mathrm{d}\Omega = \delta_{ll'}\delta_{mm'}$

$\int\mathbf{\Psi}_{lm}\cdot \mathbf{\Psi}^*_{l'm'}\,\mathrm{d}\Omega = l(l+1)\delta_{ll'}\delta_{mm'}$

$\int\mathbf{\Phi}_{lm}\cdot \mathbf{\Phi}^*_{l'm'}\,\mathrm{d}\Omega = l(l+1)\delta_{ll'}\delta_{mm'}$

$\int\mathbf{Y}_{lm}\cdot \mathbf{\Psi}^*_{l'm'}\,\mathrm{d}\Omega = 0$

$\int\mathbf{Y}_{lm}\cdot \mathbf{\Phi}^*_{l'm'}\,\mathrm{d}\Omega = 0$

$\int\mathbf{\Psi}_{lm}\cdot \mathbf{\Phi}^*_{l'm'}\,\mathrm{d}\Omega = 0$

Vektör çoklu-kutupsal momentleri

Diklik ilişkilerinin hesaplanmasında bir vektör alanının küresel çoklu kutupsal momentleri

$E^r_{lm} = \int \mathbf{E}\cdot \mathbf{Y}^*_{lm}\,\mathrm{d}\Omega$

$E^{(1)}_{lm} = \frac{1}{l(l+1)}\int \mathbf{E}\cdot \mathbf{\Psi}^*_{lm}\,\mathrm{d}\Omega$

$E^{(2)}_{lm} = \frac{1}{l(l+1)}\int \mathbf{E}\cdot \mathbf{\Phi}^*_{lm}\,\mathrm{d}\Omega$

Bir skaler alanın gradiyenti

Verilen bir skaler alanın çoklu kutupsal açılımı

$\phi = \sum_{l=0}^\infty \sum_{m=-l}^l \phi_{lm}(r) Y_{lm}(\theta,\phi)$

VSH nin terimleri içinde gradiyent yazabiliriz

$\nabla\phi = \sum_{l=0}^\infty \sum_{m=-l}^l\left(\frac{\mathrm{d}\phi_{lm}}{\mathrm{d}r} \mathbf{Y}_{lm}+ \frac{\phi_{lm}}{r}\mathbf{\Psi}_{lm}\right)$

Uzaksallık

Herhangi çok kutuplu alan için eldemiz

$\nabla\cdot\left(f(r)\mathbf{Y}_{lm}\right) = \left(\frac{\mathrm{d}f}{\mathrm{d}r}+\frac{2}{r}f\right)Y_{lm}$

$\nabla\cdot\left(f(r)\mathbf{\Psi}_{lm}\right) = -\frac{l(l+1)}{r}fY_{lm}$

$\nabla\cdot\left(f(r)\mathbf{\Phi}_{lm}\right) = 0$

Üstüstelik ile herhangi vektör alanının yakınsaklığı elde edilir

$\nabla\cdot\mathbf{E} = \sum_{l=0}^\infty \sum_{m=-l}^l \left(\frac{\mathrm{d}E^r_{lm}}{\mathrm{d}r}+\frac{2}{r}E^r_{lm}-\frac{l(l+1)}{r}E^{(1)}_{lm}\right)Y_{lm}$

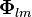$\mathbf{\Phi}_{lm}$ üzerinde gözleyebieceğimiz her zaman solenoidaldir.

Curl

herhangi çoklukutup alanı için elimizde olan

$\nabla\times\left(f(r)\mathbf{Y}_{lm}\right) =-\frac{1}{r}f\mathbf{\Phi}_{lm}$

$\nabla\times\left(f(r)\mathbf{\Psi}_{lm}\right) = \left(\frac{\mathrm{d}f}{\mathrm{d}r}+\frac{1}{r}f\right)\mathbf{\Phi}_{lm}$

$\nabla\times\left(f(r)\mathbf{\Phi}_{lm}\right) = -\frac{l(l+1)}{r}f\mathbf{Y}_{lm}-\left(\frac{\mathrm{d}f}{\mathrm{d}r}+\frac{1}{r}f\right)\mathbf{\Psi}_{lm}$

üstüstelik ile herhangi vektör alanının curl'unu elde ederiz

$\nabla\times\mathbf{E} = \sum_{l=0}^\infty \sum_{m=-l}^l \left(-\frac{l(l+1)}{r}E^{(2)}_{lm}\mathbf{Y}_{lm}-\left(\frac{\mathrm{d}E^{(2)}_{lm}}{\mathrm{d}r}+ \frac{1}{r}E^{(2)}_{lm}\right)\mathbf{\Psi}_{lm}+ \left(-\frac{1}{r}E^r_{lm}+\frac{\mathrm{d}E^{(1)}_{lm}}{\mathrm{d}r}+\frac{1}{r}E^{(1)}_{lm}\right)\mathbf{\Phi}_{lm}\right)$

Örnekler

İlk vektör küresel harmonikler

• $l=0\,$

• $\mathbf{Y}_{00}= \sqrt{\frac{1}{4\pi}}\hat{\mathbf{r}}$

• $\mathbf{\Psi}_{00}= \mathbf{0}$

• $\mathbf{\Phi}_{00}= \mathbf{0}$

• $l=1\,$

• $\mathbf{Y}_{10}= \sqrt{\frac{3}{4\pi}}\cos\theta\,\hat{\mathbf{r}}$
• $\mathbf{Y}_{11}= -\sqrt{\frac{3}{8\pi}}\mathrm{e}^{\mathrm{i}\varphi}\sin\theta\,\hat{\mathbf{r}}$

• $\mathbf{\Psi}_{10}= -\sqrt{\frac{3}{4\pi}}\sin\theta\,\hat{\mathbf{\theta}}$
• $\mathbf{\Psi}_{11}= -\sqrt{\frac{3}{8\pi}}\mathrm{e}^{\mathrm{i}\varphi}\left(\cos\theta\,\hat{\mathbf{\theta}}+\mathrm{i}\,\hat{\mathbf{\varphi}}\right)$

• $\mathbf{\Phi}_{10}= -\sqrt{\frac{3}{4\pi}}\sin\theta\,\hat{\mathbf{\varphi}}$
• $\mathbf{\Phi}_{11}= \sqrt{\frac{3}{8\pi}}\mathrm{e}^{\mathrm{i}\varphi}\left(\mathrm{i}\,\hat{\mathbf{\theta}}-\cos\theta\,\hat{\mathbf{\varphi}}\right)$

m'in negatif değer için bağıntı simetri ilişkileri uygulamaları ile elde ediliyor.

Uygulamalar

Elektrodinamikler

VSH çoklu kutupsal ışıma alanlarının çalışması içinde özellikle kullanışlıldır.Örneğin, bir manyetik çoklukutuplar 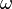$\omega\,$ açısal frekans ile bir akım salınımı ve karmaşık genliğin her ikisidir

$\hat{\mathbf{J}}= J(r)\mathbf{\Phi}_{lm}$

ve elektrik ve manyetik alanlarının karşılığı olarak yazılabilir

$\hat{\mathbf{E}}= E(r)\mathbf{\Phi}_{lm}$

$\hat{\mathbf{B}}= B^r(r)\mathbf{Y}_{lm}+B^{(1)}(r)\mathbf{\Psi}_{lm}$

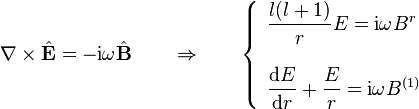
Maxwell denklemlerinde yerine koymayla, Gauss' kanunu otomatik eldesi

$\nabla\cdot\hat{\mathbf{E}}=0$

iken Faraday'ın ayırma kanunu ile

$\nabla\times\hat{\mathbf{E}}=-\mathrm{i}\omega\hat{\mathbf{B}}\qquad\Rightarrow\qquad \left\{\begin{array}{l}\displaystyle \frac{l(l+1)}{r}E = \mathrm{i}\omega B^r \\ \ \\ \displaystyle\frac{\mathrm{d}E}{\mathrm{d}r} +\frac{E}{r}= \mathrm{i}\omega B^{(1)}\end{array}\right.$

içinde

magnetik alan vurgusu için Gauss kanunu

$\nabla\cdot\hat{\mathbf{B}} = 0\quad\Rightarrow \quad\frac{\mathrm{d}B^r}{\mathrm{d}r}+\frac{2}{r}B^r - \frac{l(l+1)}{r}B^{(1)}=0$

ve Ampère-Maxwell'in de

$\nabla\times\hat{\mathbf{B}} = \mu_0 \hat{\mathbf{J}} + \mathrm{i}\mu_0\varepsilon_0\omega \hat{\mathbf{E}} \quad\Rightarrow\quad -\frac{B^r}{r}+\frac{\mathrm{d}B^{(1)}}{\mathrm{d}r}+\frac{B^{(1)}}{r} = \mu_0J+\mathrm{i}\omega\mu_0\varepsilon_0E$

Bu yol içinde, kısmi diferansiyel denklem adi diferansiyel denklemin bir kümesi içinde dönüştürülmektedir.

Akış dinamikleri

Stokes kanunu hesabında küçük küresel parçacıklar üzerine bir viskoz akışkan uygulanmasıyla sürükleneceği için böylece, Navier-Stokes denkleminin ihmali eylemsizlik hız dağılımına uyar,yani

$\nabla\cdot \mathbf{v} = 0$

$\mathbf{0} = -\nabla p + \eta \nabla^2\mathbf{v}$

sınır durumları ile

$\mathbf{v} = \mathbf{0}\quad (r=a)$

$\mathbf{v} = -\mathbf{U}_0\quad (r\to\infty)$

parçacıklardan uzak akış için parçacıkların göreli hızı 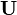$\mathbf{U}\,$ olsun.Küresel koordinatlarda sonsuzdaki bu hız:

$\mathbf{U}_0 = U_0\left(\cos\theta\, \hat{\mathbf{r}} - \sin\theta \,\hat{\mathbf{\theta}}\right) = U_0 \left(\mathbf{Y}_{10} + \mathbf{\Psi}_{10}\right)$

olarak yazılabilir.Son açılım sıvı hızı ve basınç için küresel harmonikler üzerinde bir açılım önermektedir.

$p=p(r)Y_{10}\,$

$\mathbf{v} = v^r(r) \mathbf{Y}_{10} + v^{(1)}(r) \mathbf{\Psi}_{10}$

Navier-Stokes denklemlerinde yerine konulan katsayılar adi diferansiyel denklemlerin bir kümesi ürünleridir.

Ayrıca bakınız

• Küresel harmonikler
• Spin küresel harmonikler
• Çoklukutup açılımı
• Elektromanyetik ışıma
• Küresel koordinatlar
• Küresel taban

Kaynakça

Dış bağlantılar

• Vector Spherical Harmonics at Eric Weisstein's Mathworld