Çift yarık deneyi

Young deneyi olarak da bilinen çift-yarık deneyi, ışık ve maddenin aynı anda dalga ve parçacık özellikleri sergileyebileceğini gösterir.Dalga ve parçacık özellikleri aynı anda bulunamaz. Deneyin basit versiyonunda lazer ışını gibi bağdaşık (eş fazlı) bir ışık kaynağı, iki paralel yarık açılmış ince bir levhayı aydınlatır, ve yarıktan geçen ışık levhanın arkasındaki bir ekranda gözlemlenir. Işığın dalga doğası ışık dalgalarının iki yarıktan da geçerek girişim yapmasını, ve ekranda aydınlık ile karanlık bantlar oluşturmasını sağlar, ki bu sonuç ışık tamamen parçacıklı yapıda olsa beklenemez. Fakat, parçacıklardan veya fotonlardan oluşuyormuş gibi, ekranda her zaman ışığın soğurulduğu görülür.^{[1] [2]} Bu durum dalga-parçacık ikiliği olarak bilinen prensibi ortaya koyar.

Genel bakış

Aynı çift-yarık kurulumu (yarıklar arası 0.7mm); üstteki resimde bir yarık kapalı. tek yarık girişim deseninin çift-yarıkta da görüldüğüne dikkat edin, yoğunluk iki katına çıkıyor ve birçok küçük girişim saçakları ekleniyor.

Eğer ışık tamamen sıradan parçacıklardan oluşsaydı ve bu parçacıklar bir yarıktan geçirilip ekrana çarptırılsaydı, yarığın büyüklüğüne ve şekline bağlı bir desen görürdük. Hâlbuki, tek yarık deneyi gerçekleştirildiğinde, ekrandaki desen bir dağılma desenidir, ortada dar bir merkezi bant ve ona paralel olarak dizilmiş daha karanlık bantlar olarak görünür.

Benzer şekilde, ışık sadece parçacıklardan oluşsaydı ve iki paralel yarıktan geçirilseydi, ekrandaki desen basitçe iki adet tek yarığın oluşturduğu desenlerin toplamı olurdu. Fakat gerçekte, desen daha geniş ve daha detaylı hale gelir, bir dizi aydınlık ve karanlık bant içerir. Thomas young bu olguyu ilk defa ispatladığında, ışığın dalgalardan oluştuğuna işaret ediyordu, ki aydınlık bölgelerin dağılımı dalga cephelerinin girişimiyle açıklanabilir.^[3] Young deneyi, Isaac Newton tarafından öne sürülen ve 17. ve 18. yüzyılda ışığın yayılma modeli olarak kabul edilen ışığın parçacık teorisini mağlup ederek, 1800lerin başında ışığın dalga teorisinin kabul edilmesinde çok önemli bir rol oynadı. Yine de, fotoelektrik etkisinin daha sonraki keşfi, farklı şartlar altında ışığın parçacıklardan oluşuyormuş gibi davranabileceğini gösterdi. Birbiriyle çelişiyormuş gibi görüen bu keşifler klasik fiziğin ötesine geçerek ışığın kuantum doğasını hesaba katmayı gerekli hale getirdi.

Çift-yarık deneyi ışıktan başka bir şey ile denenmemişti, ta ki1961 yılında Tübingen Üniversitesi’nden Clauss Jönsson bunu elektronlarla deneyene kadar.^[4][5] 2002 yılında, Physics World okuyucuları tarafından Jönsson’un çift-yarık deneyi ’en güzel deney’ olarak seçildi.^[6]

1999’da mikroskopta görülebilecek kadar büyük parçacıkların- buckyball molekülleri (0.7 nm çağında, protondan yarım milyon kat daha büyük)- dalga-tipi girişim sergiledikleri bulundu.^[7][8]

Çift-yarık deneyi (ve varyasyonları) kuantum mekaniğinin temel bilmecesini açıkça ortaya koyabildiği için klasik bir düşünce deneyi haline geldi. Richard Feynman, bu tek deney üzerinde dikkatlice düşünerek tüm kuantum mekaniğinin derlenebileceğini söylemiştir.^[9]

Young'ın düzeneği

Thomas Young tek ışık kaynağı olarak, iğne deliğinden geçen güneş ışığını kullanmıştır.İğne deliğinden yayılan ışık, üzerinde birbirine yakın iki iğne deliği bulunan ve deliklerin ilk kaynağa uzaklıkları eşit olacak şekilde yerleştirilen saydam olmayan bir engele düşürülür. Birinci iğne deliğinden herhangi bir anda çıkan ışık diğer iki iğne deliğinden aynı anda geçeceği için iki iğne deliğinden çıkan ışık o anda aynı fazda olur ve ekranda girişim çizgilerinin yeri değişmez; girişim saçakları gözlemlenir.

Şekil 3, girişimi meydana getiren dalgaların çizgi halindeki kaynağa ve yarıklara üstten bakılmış halini gösterir. İmgede düğüm çizgileri açıkça seçilmektedir. Bunlar dalga hareketinin ve bu nedenle ışığın bulunmadığı alanlardır; perdeyle ara kesitleri siyah olarak çizilmiştir. Perdede bir parlak bir karanlık olarak sıralanan renklerde girişim çizgileri görülmektedir. Tıpkı ışığın dalga modelinde kestirildiği gibi, ortadaki parlaktır ve bu çizgiler yarıklara paraleldir.^[10]

Dalga-parçacık ikiliğinin çift yarıkta girişim deneyiyle ve gözlemcinin etkisiyle animasyon olarak gösterilmesi

• 
  Şekil 2: Çift yarık deneyi animasyonu
• 
  Şekil 3
• 
  ekil.4 Thomas Young'un deneyinin bir krokisi
• 
  Şekil.5

Deneyin çeşitlemeleri

Ayrı parçacıkların girişimi

Zaman içinde elektron birikimi

Bu deneyin önemli bir versiyonu tek parçacıklardır(veya dalgalar, burada tutarlılık adına parçacık diyeceğiz). Çift-yarıktan tek seferde parçacıklar yollamak, bekleneceği gibi ekranda tek tek parçacıklar görmemize neden olur. Hâlbuki, bu parçacıklar teker teker gönderilirse bir girişim deseni oluşur. Örneğin, her seferinde çift-yarıktan bir elektron gönderebilen bir laboratuvar aleti yapıldığında^[11] oluşan girişim deseni, her elektronun kendisi ile girişim yaptığını ve bu yüzden iki yarıktan birden geçmesi gerektiğini^[12] gösterir-ki bu fikir ayrı objelerle olan günlük deneyimlerimizle çakışır. Bu olgunun, buckyball molekülleri gibi moleküller veya atomlar ile de gerçekleştiği gösterilmiştir.^[7][13][14] Böylece, elektronlarla yapılan deneyler Dirac’ın, elektron, proton, nötron ve hatta daha büyük varlıkların kendi dalga doğaları olduğu ve hatta kendi özel frekansları olduğu görüşünü teyit eder.

Bu deneysel gerçek tekrar türetilebilirdir ve kuantum mekaniğinin matematiği elektronun ekranda belli bir noktaya çarpma olasılığını tam olarak öngörmemizi sağlar. Fakat, elektronlar ekrana beklenen bir düzende ulaşmazlar. Diğer bir deyişle, ekranda beliren diğer tüm elektronların nerde ve hangi düzende olduğu gelecek olan elektronun nereye çarpacağı hakkında bilgi vermez, yine de belirli noktalardaki olasılıklar hesaplanabilir.^[15] Bu yüzden, girişim deseninin çok düzenli ve öngörülebilir bir formülasyonu olsa da nedensiz bir seçilim olayı görürüz. Bu bazı teorikçileri, bilindikleri takdirde hedef ile her ayrı etkileşimin konumunun sebebini gösterecek olan sistemdeki ek determinantları veya ’gizli değişkenler’ i bulmaya teşvik etmiştir.^[16]

1909 yılında Taylor tarafından^[17], gelen ışığın seviyesini foton soğurulması ve yayılması olayları çakışmayana kadar düşürerek, bir düşük-yoğunlukta çift-yarık deneyi gerçekleştirildi. Ayrı fotonlarla oluşan girişim deseni, tek bir fotonun kendi dalga cephesi olup iki yarıktan da geçtiği ve fotonun, yarıklardan geçen iki olasılık dalgasının kesişmesi ile oluşan net olasılık değerine göre dedektör ekranda görülmesi ile açıklanabilir.^[18] Dikkat edilmesi gereken bir nokta, toplanan veya birbirini yok eden değerin, ekrandaki çeşitli noktalarda görülen foton olasılığı değil genliği olmasıdır. Eğer bir noktada dalgaların birbirini yok etmesi varsa, bu fotonun yokolduğunu göstermez; sadece o noktada fotonun belirmesi olasılığının azaldığını ve başka bir noktada arttığını belirtir.

Kuantum mekaniğinde çift-yarık deneyinin matematiğine detaylı bir yaklaşım Englert-Greenberger ikiliği konusundaki makalede yer alır.

Yarıklarda parçacık dedektörleri olması

Çift-yarık düzeneği yarıklara parçacık dedektörleri yerleştirilerek değiştirilebilir. Bu deneyi yapan kişinin parçacığın ekrana çarptığında değil yarıklardan geçerkenki konumunu bulmasını sağlar- parçacığın yapacağı gibi tek bir yarıktan mı geçti, yoksa dalganın yapacağı gibi her ikisinden de mi? Sayısız deney göstermiştir ki, parçacığın hangi yarıktan geçeceğini tayin eden herhangi bir değişiklik eklenmesi ekrandaki girişim deseninin görünürlüğünü azaltır^[3], ve bütünleyicilik prensibini aydınlatır: ışık (ve elektronlar, vb.) parçacık veya dalga gibi davranabilir, fakat aynı anda ikisi de olmaz.^[19][20][21] 1987’de yapılan bir deney girişim desenini bozmadan bir parçacığın hangi yolu izlediği hakkında bilgi edinilebileceğini gösteren sonuçlara ulaştı.^[22] Bu da parçacıklara daha düşük bir seviyede dokunmanın girişim desenini ufak bir çapta etkilediği ölçümlerin etkisini gösterir.

Bir fotonun bir yarıktan geçip geçmediğine karar vermenin birçok yöntemi vardır, örneğin, her yarığıa bir tane atom yerleştirilebilir. Bu tipte deneyler foton^[22] ve nötronlarla^[23] yapılmıştır.

Geç seçim ve kuantum silme çeşitlemeleri

Geç-seçim deneyi ve kuantum silme, çift-yarık deneyinde dedektörlerin yarıklardan başka yerlere yerleştirilmiş çeşitleridir. İlki, bir parçacık yarıktan geçtikten sonra hangi yolu izlediği bilgisinin elde edilmesinin, yarıklarda daha önceki davranışını geriye dönük olarak etkileyebildiğini gösterir. İkincisi, dalga davranışının, hangi yolun izlendiği bilgisinin silinmesi ile geri kazanılabileceğini gösterir.

Diğer çeşitler

Bir laboratuvar çift-yarık düzeni; üst sütunlar arası uzaklık bir inç civarında.

1967’de Pfleegor ve Mandel, ışık kaynakları olarak iki lazer kullanarak çift-kaynak girişimi yaptılar.^[24][25]

1972’de deneysel olarak, sadece bir yarığın her zaman açık olduğu bir çift-yarık deneyinde, yol farkı fotonun her iki yarıktan da gelebileceği gibi olduğu sürece girişimin gözleneceği ortaya konmuştur.^[26][27] Bu deneysel şartlarda sistemdeki foton yoğunluğu bir birimden azdı. Deney, C60 kadar büyük parçacıklar ile gerçekleştirildi.^[28]

Matematiksel analiz

Klasik dalga-optiği formülasyonu

Klasik dalga teorisi kullanılarak ışığın birçok davranışı modellenebilir. Bu modellerden biri Huygens-Fresnel prensibidir; dalga cephesindeki her noktanın ikinci bir küresel dalga yarattığını ve takip eden bir noktadaki bir bozulmanın bu noktada oluşturduğu katkıların toplanmasıyla bulunabileceğini söyler. Bu toplam ayrı dalgacıkların genlikleri kadar fazlarını da hesaba katmalıdır. Şunu da not etmek gerekir ki bir ışık alanının sadece yoğunluğu ölçülebilir- genliğin karesiyle orantılıdır.

Çift-yarık deneyinde, iki yarık tek bir lazer ışınıyla aydınlatılır. Eğer yarık genişliği yeterinde küçükse(lazer ışığının dalgaboyundan küçük), yarıklar ışığı silindirik dalgalar ayırır. Bu iki silindirik dalga cephesi ilave edilir, ve herhangi bir noktadaki genlik ile yoğunluk bu iki dalgacephesinin hem büyüklüğüne hem de fazlarına bağlıdır. iki dalga arasındaki faz farkı iki dalganın aldığı yolların farkı ile bulunur.

Görüş mesafesi yarıklar arası uzaklıktan çok fazla ise, faz farkı aşağıda gösterilen şekildeki geometri ile bulunur. θ açısı ile hareket eden iki dalga arasındaki yol farkı:

${\displaystyle d\sin \theta \approx d\theta }$

İki dalga aynı fazda ise, diğer bir deyişle yol farkı dalgaboyunun tam katları ise, toplanan genlik ve yoğunluk maksimum olur, eğer zıt fazda iseler, yani yol farkı dalgaboyunun yarısının katları ise iki dalga birbirini yok eder ve bulunan yoğunluk sıfır olur. Bu etki girişim olarak bilinir. Maksimum değerde girişim saçağı şu açılarda olur:

${\displaystyle ~d\theta _{n}=n\lambda ,~n=0,1,2,\ldots }$

λ ışığın dalgaboyunun gösterir. Saçaklar arası açısal boşluk θ_f ise;

${\displaystyle \theta _{f}\approx \lambda /d}$

Yarıklardan z kadar uzaktaki saçaklar arası boşluk:

${\displaystyle ~w=z\theta _{f}=z\lambda /d}$

Örneğin, iki yarık 0.5mm kadar ayrı ise ve 0.6 μm lik dalgaboyunda bir lazerle aydınlatılıyorsa, 1 metre uzaktan bakıldığında saçaklar arası uzaklık 1.2m olur.

Yarık genişliği,b, dalgaboyundan büyükse Fraunhofer dağılım denklemi dağılan ışığın yoğunluğunu şöyle verir:^[29]

${\displaystyle {\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi d\sin \theta }{\lambda }}\right]~\mathrm {sinc} ^{2}\left[{\frac {\pi bsin\theta }{\lambda }}\right]\end{aligned}}}$

Yukarıdaki resimde ilk desen tek yarık ile oluşan girişim desenidir,fonksiyonda sincile verilmiştir. İkinci şekil iki yarıktan girişimin toplam yoğunluğunu gösterir, cos fonksiyonu ayrıntılı yapıyı temsil eder, ve kaba yapı ise iki yarığın ayrı ayrı girişim desenlerini gösterir.

Daha yakın alan için benzer hesaplamalar Fresnel dağılım denklemi ile yapılabilir. Gözlem düzlemi yarık düzlemine yaklaştıkça, her yarık için dağılım deseni boyut olarak küçülür, böylece girişimin olduğu alan azalır ve iki dağılım deseninde üstüste binme yoksa yokolur.^[30]

Formüller

Young deneyinde aydınlık ve karanlık saçaklar

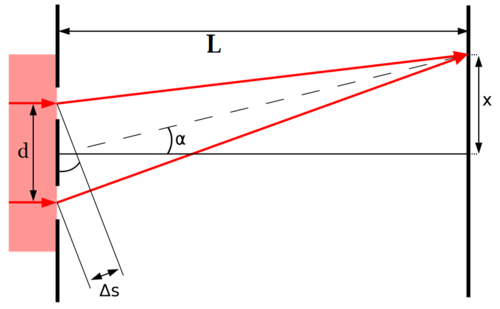
Ekran üzerinde herhangi bir noktanın merkezi aydınlık saçağa olan dik uzaklığı (X)

${\displaystyle X={\frac {\Delta S\cdot L}{d\cdot n}}}$

Burada;

${\displaystyle X\,}$: Ekran üzerinde herhangi bir noktanın merkezi aydınlık saçağa olan dik uzaklığı,

${\displaystyle \Delta S\,}$: Ekran üzerinde herhangi bir noktanın yarıklara olan uzaklıkları farkı,

${\displaystyle L\,}$: Fant ile ekran arasındaki uzaklık,

${\displaystyle d\,}$: Yarıklar arasındaki uzaklık,

${\displaystyle n\,}$: Fant ile ekran arası ortamın ışığı kırma indis'idir (birimi yok).

Not: Bu formülde Uzunluk birimleri, aynı cinsten olmalıdır.

Herhangi bir aydınlık saçağın numarası (k)

${\displaystyle k={\frac {\Delta S}{\lambda }}}$

Burada;

${\displaystyle k\,}$: Aydınlık saçağın numarası (Kaçıncı aydınlık saçak olduğunu gösterir.), birimi yok, k=0, 1, 2, 3, ...olmalıdır

${\displaystyle \Delta S\,}$: Ekran üzerinde herhangi bir noktanın yarıklara olan uzaklıkları farkı,

${\displaystyle \lambda \,}$: Kullanılan ışığın dalga boyu'dur.

Not: Bu formülde Uzunluk birimleri, aynı cinsten olmalıdır.

Herhangi bir karanlık saçağın numarası (k)

${\displaystyle k={\frac {\Delta S}{\lambda }}-{\frac {1}{2}}}$

Burada;

${\displaystyle k\,}$: Karanlık saçağın numarası (Kaçıncı karanlık saçak olduğunu gösterir.), birimi yok, k=1, 2, 3, 4, ...olmalıdır

${\displaystyle \Delta S\,}$: Ekran üzerinde herhangi bir noktanın yarıklara olan uzaklıkları farkı,

${\displaystyle \lambda \,}$: Kullanılan ışığın dalga boyu'dur.

Not: Bu formülde Uzunluk birimleri, aynı cinsten olmalıdır.

Saçak aralığı formülü

Ekran üzerindeki girişim deseninde, ard arda gelen aynı cins iki saçak arasındaki uzaklığa saçak aralığı ya da saçak genişliği denir.

2. Tanım: Herhangi bir saçağın ekran üzeindeki genişliğine denir. Yani saçak genişliği anlamına gelir. Çift yarıkta girişimde bütün saçakların boyu birbirine eşittir.

${\displaystyle x_{S.G.}={\frac {\lambda \cdot L}{d\cdot n}}}$

Burada;

${\displaystyle x_{S.G.}\,}$: Örneğin; birinci karanlık saçak ile ikinci karanlık saçak arasındaki uzaklık,

${\displaystyle \lambda \,}$: Kullanılan ışığın dalga boyu,

${\displaystyle L\,}$: Fant ile ekran arasındaki uzaklık,

${\displaystyle d\,}$: Yarıklar arasındaki uzaklık,

${\displaystyle n\,}$: Fant ile ekran arası ortamın ışığı kırma indis'idir (birimi yok).

Not: Bu formülde Uzunluk birimleri, aynı cinsten olmalıdır.

Detaylar

Deneyin sonuçları

• İki yarığın;büyük ve birbirinden uzak olması halinde ekranda üst üste iki ışık lekesinin oluşturduğu;birbirine yakın delikler küçük olduğunda isegirişim saçakları adı verilen renk şeritlerinin oluştuğunu gördü.Bu renkli şeritler yalnızca dalgaların ürettiğini ortaya koydu.
• Yarıkların biri kapatılırsa girişim deseni kaybolur ve yarığın arkasında sadece bir çizgi oluşur.
• Herhangi bir yöntemle, ışık ya da parçacığın hangi yarıktan geçtiği tespit edilmeye çalışılırsa o anda girişim deseni kaybolur ve yarığın arkasında iki ayrı çizgi oluşur.
• Işık ya da parçacığın, çift yarıklı levha arkasında, bilinen fizik kurallarına göre iki çizgi oluşturması gerekirken, neden girişim deseni oluştuğunun tespitine çalışılması, deneyin sonucunu anlaşılmaz bir şekilde değiştirir, bu sonuç bilim tarihinin belki de en büyük açmazını oluşturur. Çünkü herhangi bir ölçüm girişimi, deneyin sonucunu değiştirerek gözlem yapılmasını engeller.
• Kararlı girişim deseni oluşturabilmek için her bir dalga birbirlerine olan sabit fazı korumalıdırlar.^[31]

Deneyin gerçekleştirilebilmesi için önşartlar

• Yarıktan geçirilen ışığın tek renkli, yani mümkün olduğunca aynı dalga boyunda olması gerek.Çünkü eğer farklı renkli yani farklı dalga boylu ışıklar kullanılırsa ekranda sürekli kayan bir girişim deseni oluşur.bu da karanlık ve aydınlık sacakların net olarak farkedilememesine neden olur.
• Kaynaklar uyumlu yani eş fazlı(koherent)olmalıdır,kısaca sabit fazı korumalıdırlar birbirlerine göre.^[32]
  • Koherent kaynaklarında:iki kaynağa (hareketli dalga üreten) iki kaynağa ihtiyaç duyulur.Ayrıca,kararlı girişim deseni oluşturabilmek için her dalga birbirine göre sabit olan fazı korumalıdır.bu durum elde edildiğinde sonuca koherent yahut eş fazlı kaynaklar denir.Örneğin,bir tek giriş ile beslenen yan yana yayınlanan iki hoparlörden ses dalgaları oluşturulabilir.çünkü bu iki hoparlör aynı yolla,aynı zamanda,yükseltilip,aynı tepkide bulunurlar.^[33]
• Kaynaklar tek renkli,yani tek dalga boylu olmalıdır.
  • Rastgele iki kaynağı ele alınır:Bu iki ışık kaynağı yan yana olduğunda girişim olayı hiç gözlenmez;Bu durumda kaynaklar birbirinden yayınlanan ışık dalgaları bağımsız olarak bulunmaktadır.Böylece,kaynakların yaydıkları dalgalar ,gözlem süreci boyunca birbirlerine göre sabit faz ilişkisini korumazlar.^[34].Adi bir ışık kaynağından çıkan ışık yaklaşık olarak 10⁻⁸s de rastgele bu tür delikler sergiler.Bundan dolayı,yok edici,yapıcı veya bir ara durum girişim koşılları ancak 10⁻⁸kadarlık bir zamanda gerçekleşir.Bu esnada hiçbir girişim olayı gözlenmez,çünkü göz böyle kısa süreli değişimleri takip edemez.Bu tür uyumsuz ışık kaynaklarına (yahut koherent değildir) denir.
• Üstüste binme ilkesi uygulanabilmelidir.
  • Eş fazlı ışık kaynağını elde etmek için yaygın bir metod,genellikle yarık biçiminde bir levhayı aydınlatmak için tek renkli bir kaynak kullanmaktır.İki yarıktan geçen ışık eş fazladır,çünkü bir tek kaynak özgün ışık demeti üretiyor ve levhada sadece özgün demeti iki parçaya ayırma işlemini yapıyor.Kaynaktan yayılan ışık rastgele bir değişim gösterse bile aynı zamanda iki ayrı demet getirilirse girişim olayları hala gözlenebilir.
• Girişim deneyinin iyi gözlenebilmesi için L/d oranı cok büyük olmalıdır yoksa karanlık ve aydınlık saçak tam olarak belli olmaz.

Deneyin özellikleri

• Işığın dalga boyu artarsa saçak genişliği artar
• Kaynaklar arası uzaklık artarsa ∆X azalır
• Saçak aralığı kaynakla çift yarık arasındaki uzaklığa ve ışığın şiddetine bağlı değildir.
• Yarıklar düzlemiyle perde arasındaki uzaklık artarsa ∆X artar
• Çift yarıkla perde arasına havadan daha yoğun bir madde koyulursa dalga boyu küçüleceğinden saçak genişliği de küçülür. Young deneyi beyaz ışıkla yapılınca desende renklenmeler olur.

Bu durum;

• Beyaz ışığın 7 renkten oluştuğunu
• Saçak aralığının dalga boyuna eşit olduğunu
• Her rengin kendine özgü dalga boyu olduğunu açıklar.

Deneyin yorumlanması

Schrödinger’in kedisi düşünce deneyinde olduğu gibi, çift-yarık deneyi kuantum mekaniğinin çeşitli yorumlanmaları arasındaki fark ve benzerlikleri açığa kavuşturmakta kullanılır.

Kopenhag yorumu

Kopenhag yorumu, matematiksel formüllerin ve atomik seviyede neler olup bittiği hakkında bilgi edinmemizi sağlayan fiziksel tepkime ve aletlerin ötesinde olanı varsaymanın istenmeyen bir şey olduğunu söyleyen, kuantum mekaniğini alanındaki takipçilerin bir uzlaşmasıdır. Deneycilerin belli deney sonuçlarını doğru tahmin etmelerine olanak sağlayan matematiksel yapılardan biri olasılık dalgasıdır. Matematiksel formunda, fiziksel dalga tanımı ile benzerdir, fakat burada tepe ve çukurlar sıradan insan deneyiminin makro dünyasında gözlenebilen belli bir olayın meydana gelme olasılığının düzeylerini ifade eder.

Olasılık dalgasının uzaydan geçebildiği söylenir çünkü matematiksel gösteriminden hesaplanan olasılık değerleri zamana bağımlıdır. Foton gibi bir parçacığın yayıldığı ve tespit edildiği zaman arasındaki konumunu bilemeyiz, çünkü bir şeyin belli bir zamanda belli bir yerde konumlandığını söylemek için bunu tespit etmek gerekir. Girişim deseninin son görünümü parçacıkların saçılmasını ve parçacığın saçıcıdan dedektör ekrana kadar taşınmasında en azından iki ayrı yol olmasını gerektirir. Deneylerde parçacığın saçılma zamanı ile dedektör ekrana gelme zamanı arasında hiçbir şey gözlenmez. Işık dalgası(klasik fizikteki haliyle) iki yolu da izleyecek kadar geniş olabilecekmiş gibi bir ışın izleme yapılırsa, aygıttan birçok parçacık geçip yavaş yavaş beklenen girişim desenini boyadığında bu ışın izleme kesin olarak dedektör ekrandaki minimum ve maksimum konumlarını tahmin edebilir.

Yol-integrali formülasyonu

Feynman yol-integralinde kullanılan eşit olasılıktaki sayısız yoldan biri.

Kopenhag yorumu kuantum mekaniğinin Feynman tarafından bulunan yol-integrali formülasyonuna benzerdir. Yol-integrali formülasyonu bir sistem için klasik tek-rota kavramını, tüm olası rotaların toplamı ile değiştirir. Rotalar fonksiyonel integral kullanılarak eklenir. Her rota eşit olasılıkta kabul edilir ve bu yüzden her rotanın aynı miktarda katkısı vardır. Fakat, rota boyunca verilen herhangi bir noktada bu katkının fazı, rota boyunca yapılan faaliyet ile bulunur (bkz. Euler formülü):

${\displaystyle A_{path}(x,t)=e^{iS(x,t)}}$

Bütün bu katkılar eklenir ve sonucun büyüklüğünün karesi alınır, böylece parçacığın konumu için olasılık dağılımı bulunur:

${\displaystyle p(x,t)\propto \left\vert \int _{allpaths(x,t)}e^{iS(x,t)}\right\vert ^{2}}$

Bütün olasılık hesaplamalarında olduğu gibi sonuç normalize edilir:

${\displaystyle \int _{x\in X}p(x,t)\,dx=1}$

Özetlersek, sonucun olasılık dağılımı, orijin noktasından bitiş noktasına kadarki tüm rotalar üzerinde her rota boyunca faaliyete orantılı olarak hareket eden dalgaların süperpozisyonlarının normunun normalize edilmiş karesidir. Farklı rotalar üzerindeki faaliyetler arasındaki farklar(katkıların bağıl fazları) çift-yarık deneyinde gözlenen girişim desenini oluşturur. Feynman bu formülasyonun matematiksel bir tanım olduğunu, ölçemeyeceğimiz gerçek bir işlemi tanımla girişimi olmadığını vurgulamıştır.

İlişkisel yorum

Kuantum mekaniğinin ilk olarak Carlo Rovelli^[35] tarafından yapılan ilişkisel yorumuna göre, çift-yarık deneyindeki gibi gözlemler özellikle gözlemci ile (ölçüm aleti) gözlemlenen(fiziksel olarak ölçülen) arasındaki etkileşimden kaynaklanır, bu obje tarafından gösterilen bir özellik değildir. Elektronu ele alırsak, ilk olarak belli bir yarıkta gözlenir, daha sonra gözlemci-parçacık etkileşimi elektronun konumu hakkında bilgi verir. Bu kısmi olarak ekrandaki son konumunu sınırlar. Eğer belli bir yarıkta değil de ekranda gözlendiyse(foton ile ölçüldüyse) etkileşimin bir parçası olan ‘’hangi rota’’ bilgisi yoktur, bu yüzden elektronun ekrandaki konumu olasılık fonksiyonu ile elde edilir. Bu da ekranda oluşan deseni her elektronun iki yarıktan da geçtiğindeki gibi yapar. Uzay ve mesafe ilgili olduğundan elektronun aynı anda iki yerde bulunabileceği de öne sürülmüştür, çünkü ekrandaki belli noktalarla olan uzaysal ilişkisi iki yarık için de aynıdır.^[36]

Kaynakça

1. Feynman, Richard P. (1965). The Feynman Lectures on Physics, Vol. 3. USA: Addison-Wesley. s. 1–8. ISBN ISBN 0201021188P. 
2. Darling, David (2007). "Wave - Particle Duality". The Internet Encyclopedia of Science. The Worlds of David Darling. 
3. Feynman, Richard P.; Robert Leighton, Matthew Sands (1965). The Feynman Lectures on Physics. Massachusetts, USA: Addison-Wesley. s. 1–1 to 1–9. ISBN 0201021188P. 
4. Jönsson C,(1961) Zeitschrift für Physik, 161:454–474
5. Jönsson C (1974). Electron diffraction at multiple slits. American Journal of Physics, 4:4–11.
6. "The most beautiful experiment". Physics World 2002.
7. New Scientist: Quantum wonders: Corpuscles and buckyballs, 2010 (Introduction, subscription needed for full text, quoted in full in )
8. Nature: Wave–particle duality of C₆₀ molecules, 14 October 1999. Abstract, subscription needed for full text
9. Greene, Brian (1999). The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. New York: W.W. Norton. s. 97–109. ISBN 0393046885. 
10. Uri Haber- Schaim (v.d. Çev: M.Fuat Turgut, Ayhan Zeren), PSSC fizik 1-2 ,Milli Eğitim Bakanlığı,1972,İstanbul,sayfa = 148-151
11. O Donati G F Missiroli G Pozzi May 1973 An Experiment on Electron Interference American Journal of Physics 41 639–644
12. Brian Greene, The Elegant Universe, p. 110
13. http://prl.aps.org/abstract/PRL/v87/i16/e160401
14. Nairz O, Arndt M, and Zeilinger A. Quantum interference experiments with large molecules. American Journal of Physics, 2003; 71:319–325. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000071000004000319000001&idtype=cvips&gifs=yes
15. Brian Greene, The Elegant Universe, p. 104, pp. 109–114
16. Greene, Brian (2004). The Fabric of the Cosmos: Space, Time, and the Texture of Reality. Knopf. s. 204–213. ISBN 0375412883. 
17. Sir Geoffrey Ingram Taylor, "Interference Fringes with Feeble Light", Proc. Cam. phil. Soc. 15, 114 (1909).
18. de Broglie, Louis (1953). The revolution in physics; a non-mathematical survey of quanta. Translated by Ralph W. Niemeyer. New York: Noonday Press. pp. 47, 117, 178–186.
19. Harrison, David (2002). "Complementarity and the Copenhagen Interpretation of Quantum Mechanics". UPSCALE. Dept. of Physics, U. of Toronto. 3 Mart 2016 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20160303183700/http://www.upscale.utoronto.ca/GeneralInterest/Harrison/Complementarity/CompCopen.html. Erişim tarihi: 2008-06-21. 
20. Cassidy, David (2008). "Quantum Mechanics 1925–1927: Triumph of the Copenhagen Interpretation". Werner Heisenberg. American Institute of Physics. 14 Ocak 2016 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20160114094044/https://www.aip.org/history/heisenberg/p09.htm. Erişim tarihi: 2008-06-21. 
21. Boscá Díaz-Pintado, María C. (29–31 March 2007). "Updating the wave-particle duality". 15th UK and European Meeting on the Foundations of Physics. Leeds, UK. http://philsci-archive.pitt.edu/archive/00003568/. Erişim tarihi: 2008-06-21. 
22. P. Mittelstaedt; A. Prieur, R. Schieder (1987). "Unsharp particle-wave duality in a photon split-beam experiment". Foundations of Physics 17 (9): 891–903. Bibcode 1987FoPh...17..891M. DOI:10.1007/BF00734319.  Also D.M. Greenberger and A. Yasin, "Simultaneous wave and particle knowledge in a neutron interferometer", Physics Letters A 128, 391–4 (1988).
23. J. Summhammer; H. Rauch, D. Tuppinger (1987). "Stochastic and deterministic absorption in neutron-interference experiments.". Phys. Rev. A 36 (9): 4447. Bibcode 1987PhRvA..36.4447S. DOI:10.1103/PhysRevA.36.4447. PMID 9899403. 
24. Pfleegor, R. L. and Mandel, L. (July 1967). "Interference of Independent Photon Beams". Phys. Rev. 159 (5): 1084–1088. Bibcode 1967PhRv..159.1084P. DOI:10.1103/PhysRev.159.1084. 
25. http://scienceblogs.com/principles/2010/11/interference_of_independent_ph.php>
26. Sillitto, R.M. and Wykes, Catherine (1972). "An interference experiment with light beams modulated in anti-phase by an electro-optic shutter". Physics Letters A 39 (4): 333–334. Bibcode 1972PhLA...39..333S. DOI:10.1016/0375-9601(72)91015-8. http://www.sciencedirect.com/science/article/pii/0375960172910158. 
27. http://www.sillittopages.co.uk/80rms_35.html "To a light particle"
28. Wave Particle Duality of C60
29. Jenkins FA and White HE, Fundamentals of Optics, 1967, McGraw Hill, New York
30. Longhurst RS, Physical and Geometrical Optics, 1967, 2nd Edition, Longmans
31. Keller, Frederick J. ; W. Edward Gettys, Malcolm J. Skove ; Çev.: R. Ömür Akyüz,Fizik : Dalgalar, katılar ve akışkanlar, termodinamik ve optik ,Literatür Yayıncılık, 2006,İstanbul,sayfa= 912-916,isbn =975-04-0351-7
32. Serway, Raymond A. ; Raymond A. Serway ; Çev. Kemal Çolakoğlu,Fen ve mühendislik için fizik (modern fizik ilaveli)2:Elektrik manyetizma ve optik,Palme Yayıncılık,1996,Ankara,sayfa=1048-1050,ısbn =9757477184
33. Serway, Raymond A. ; Raymond A. Serway ; Çev. Kemal Çolakoğlu , Fen ve mühendislik için fizik (modern fizik ilaveli)2:Elektrik manyetizma ve optik ,Palme Yayıncılık,1996,Ankara,sayfa=1048-1050,isbn =9757477184
34. Fishbane, Paul M. ; Stephen Gasiorowicz, Stephen T. Thornton ; Ya. Haz.: Cengiz Yalçın,Temel fizik,Arkadaş Yayınevi, 2.baskı,2007,Ankara,sayfa = 1025-1027,isbn =: 978-975-509-369-7
35. Rovelli, Carlo (1996). "Relational Quantum Mechanics". International Journal of Theoretical Physics 35 (8): 1637–1678. arXiv:quant-ph/9609002. Bibcode 1996IJTP...35.1637R. DOI:10.1007/BF02302261. 
36. Filk, Thomas (2006). "Relational Interpretation of the Wave Function and a Possible Way Around Bell’s Theorem". International Journal of Theoretical Physics 45: 1205–1219. arXiv:quant-ph/0602060. Bibcode 2006IJTP...45.1166F. DOI:10.1007/s10773-006-9125-0. http://www.springerlink.com/content/v775765467462313/. 

Dış bağlantılar

• Java demonstration of double slit experiment, animated
• Java demonstration of double slit experiment, point by point
• Java demonstration of Young's double slit interference
• Double-slit experiment animation
• Caltech: The Mechanical Universe, chapter 50 – Particles and Waves
• Make your own double-slit apparatus
• Electron Interference movies from the Merli Experiment (Bologna-Italy, 1974)
• Movie showing single electron events build up to form an interference pattern in double-slit experiments. Several versions with and without narration (File size = 3.6 to 10.4 MB) (Movie Length = 1m 8s)
• Freeview video 'Electron Waves Unveil the Microcosmos' A Royal Institution Discourse by Akira Tonomura provided by the Vega Science Trust
• Hitachi website that provides background on Tonomura video and link to the video
• Simple Derivation of Interference Conditions
• Carnegie Mellon department of physics, photo images of Newton's rings
• "Single-particle interference observed for macroscopic objects"
• Huygens and interference
• Huygens and interference
• A simulation that runs in Mathematica Player, in which the number of quantum particles, the frequency of the particles, and the slit separation can be independently varied
• Wave Nature Of Light (High School Level) – Lots of graphics and simulations; double-slit equation with examples
• To a light particle