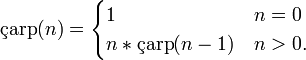Özyineleme

Yinelge (özyineleme), en genel anlamıyla bir yapının (kendi kendine) yinelenmesidir. Özellikle matematik ve bilgisayar biliminde kullanılır. Bu yapılara yinelgen yapılar denir. Yinelgen bir yapı eğer kendine gönderme yapma (atfıta bulunma) özelliğiyle yinelgen ise bu tür yapılara özgöndergeli ya da kendine-göndergeli yapılar denir.

Matematik ve mantıkta yinelgen yapılar

Yinelgen göndermeler (fonksiyonlar)

Matematiksel göndermeler (fonksiyonlar) yinelgen olarak tanımlanabilir. Örneğin doğal sayılarda tanımlı faktöriyel (çarpansal) göndermesi:

$\text{çarp}(n)= \begin{cases} 1 & n = 0 \\ n*\text{çarp}(n-1) & n > 0. \\ \end{cases}$

Doğal sayılar

Aslında matematikte sadece göndermeler değil, kümeler dahil birçok kavram yinelgen olarak tanımlananır. Örneğin doğal sayılar kümesi aşağıdaki iki özelliği sağlayan en küçük kümedir:

1. 0 bir doğal sayıdır.
2. n bir doğal sayı ise n+1 bir doğal sayıdır.

Tümevarım

Yaygın bir matematiksel kanıt çeşidi olan tümevarım çoğu zaman yinelgeye baş vurur. Örneğin Osman soyundan gelenlerin insan olduğu iki temel varsayım ile ispatlanabilir.

Varsayım 1: Osman insandır.

Varsayım 2: İnsanın çocuğu insandır.

İddia: x, Osman soyundan geliyor ise insandır.

İspat:

Temel durum: x, Osman ise insandır (Varsayım 1).

Tümevarım adımı: 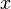$x$'in ebeveyni Osman ise temel durum ve Varsayım 2'ye göre kendisi de insandır. x, Osman soyundan geliyor fakat 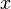$x$'in ebeveyni Osman değilse, 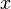$x$'in ebeveyni Osman soyundan geliyordur ve İddiaya göre ebeveyni insandır. Bu durumda Varsayım 2'ye göre x de insandır.

Kendi kendine atıfta bulunan bu ispat şekli, temel durum haricindeki her durum için bir önceki durumun doğru olduğunu kabul etmektedir. Örneğin 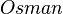$Osman$'ın torunu 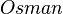$Osman$'ın çocuğu insan olduğu için insandır. 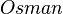$Osman$'ın çocuğu ise Osman insan olduğu için insandır. Herhangi bir nesilden bu şekilde geriye gidilebilir.

Bilgisayar programlarında yinelgen yapılar

İşlev tanımlama

Matematiktekine benzer şekilde, işlevler yinelgen olarak tanımlanabilir. Örneğin işlevsel bir programlama dili olan Common Lisp'te faktöriyel işlevi aşağıdaki gibi tanımlanabilir:

(defun fak(n)
  (if (<= n 1) 1
    (* n (fak (- n 1)))))

Ya da daha yaygın olarak kullanılan C dilinde;

int fak(int n)
{
 if (n<=1) return 1;
 return n*fak(n-1); 
}

Church tezine göre hesaplanabilir bütün işlevler, yinelgen işlevler ile ifade edilebilir.

Veri türleri

Bazı programlama dilleri, yinelgen veri türlerine izin verir. Aşağıdaki betik parçası, Ocaml'de doğal sayı veri tipini tanımlamaktadır:

type dogal = SIFIR | SONRAKI of dogal

---

Ayrıca doğal ve yapay dillerin sözdizimleri ve dilbilgileri de yinelgen tanımlanabilir.