Bağlantı (karma demet)
Karma demet 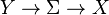 simetri kırılması ile ölçek teorisi içinde önemli bir rol oynar,örneğin, ölçü gravitasyon teorisi, Otonom olmayan mekanik burada
simetri kırılması ile ölçek teorisi içinde önemli bir rol oynar,örneğin, ölçü gravitasyon teorisi, Otonom olmayan mekanik burada 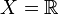 zaman eksenidir., yani,zaman-bağımlı parametrelerle mekanik, vb. Burada lif demetleri
zaman eksenidir., yani,zaman-bağımlı parametrelerle mekanik, vb. Burada lif demetleri 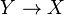 ,
, 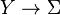 ve
ve 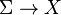 üzerinde bağlantılar arasındaki ilişkiler önemlidir .
üzerinde bağlantılar arasındaki ilişkiler önemlidir .
Karma demet
diferansiyel geometride bir karma demet ile bileşim anlamına
lif demetlerinin
Bu demet koordinatları 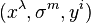 ile sağlanır, burada
ile sağlanır, burada 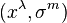 bir
bir 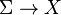 lif demeti üzerinde koordinatlardır ,yani
lif demeti üzerinde koordinatlardır ,yani 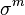 koordinatlarının geçiş fonksiyonları bağımsız
koordinatlarının geçiş fonksiyonları bağımsız 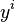 koordinatlarınındır.
koordinatlarınındır.
Aşağıda gerçek karma demetlerinin yukarıda belirtilen fiziksel uygulamaları sağlanmaktadır. karma demet göz önüne alındığında (1), 
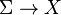 eğer varsa bir lif demetinin küresel bir bölüm olmasına izin verir.geri çekme demeti ise
eğer varsa bir lif demetinin küresel bir bölüm olmasına izin verir.geri çekme demeti ise
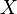 üzerinde
üzerinde 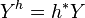 bir
bir 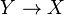 lif demetinin bir alt demetidir.
lif demetinin bir alt demetidir.
Karma temel demet
Örneğin , diyelimki 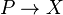 bir temel demet olsun, bir
bir temel demet olsun, bir  Lie grup yapısı ile bu bir kapalı altgrup
Lie grup yapısı ile bu bir kapalı altgrup 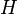 için indirgenebilirdir. Burada bir karma demet
için indirgenebilirdir. Burada bir karma demet 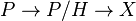 ve burada
ve burada 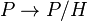 bir temel demet ile bir yapı grubu
bir temel demet ile bir yapı grubu 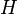 ve
ve 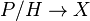 bir lif demeti
bir lif demeti 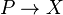 ile ilişkilidir. Verilen
ile ilişkilidir. Verilen 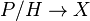 nin bir global kesiti
nin bir global kesiti  dir,geri çekme demeti
dir,geri çekme demeti 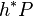 bir
bir 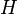 yapı grubu ile bir
yapı grubu ile bir 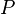 nin indirgenmiş temel altdemetidir.ölçü teorisinde,
nin indirgenmiş temel altdemetidir.ölçü teorisinde, 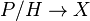 nin kesiti klasik Higgs alanları olarak işlenir.
nin kesiti klasik Higgs alanları olarak işlenir.
Bileşik demetinin jet manifoldları
Verilen karma demet 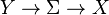 (1),diyelimki
(1),diyelimki 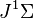 ,
, 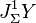 jet manifoldlardır, ve sırasıyla
jet manifoldlardır, ve sırasıyla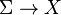 nin lif demetleri
nin lif demetleri 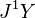 ,
, 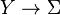 , ve
, ve 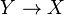 , düşünüyoruz.Bunlar uyarlanmış
, düşünüyoruz.Bunlar uyarlanmış 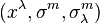 ,
, 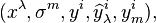 , ve
, ve 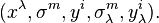 koordinatlar ile sağlanır
koordinatlar ile sağlanır
kurallı eşlemesi vardır
-
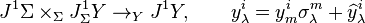 .
.
Karma bağlantı
Bu kanonik lif demetine bağlantılar arasında ilişkileri 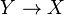 ,
, 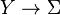 ve
ve 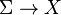 tanımlar.Bu bağlantılar ilgili tanjant değerli bağlantı formları tarafından verilmektedir.
tanımlar.Bu bağlantılar ilgili tanjant değerli bağlantı formları tarafından verilmektedir.
bir lif demeti 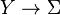 üzerinde bir bağlantı
üzerinde bir bağlantı 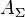
ve bir lif demeti 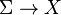 üzerinde bir bağlantı
üzerinde bir bağlantı
bir karma demet 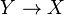 üzerinde
üzerinde 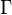 bir bağlantı tanımlanıyor.
bir bağlantı tanımlanıyor.
Buna karma bağlantı denir.Bu böylece 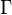 bağlantısının aracılığıyla
bağlantısının aracılığıyla 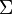 üzerinde
üzerinde 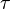 nun yatay kaymalarının
nun yatay kaymalarının 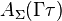 düzeni ile çakışma
düzeni ile çakışma 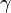 karma bağlantının aracılığıyla
karma bağlantının aracılığıyla 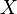 üzerinde bir vektör alanı
üzerinde bir vektör alanı 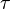 nun
nun 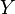 üzerinde yatay kaldırma
üzerinde yatay kaldırma 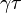 ve bir
ve bir 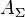 bağlantısının aracılığıyla
bağlantısının aracılığıyla 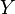 üzerinde ise bir teklik bağlantısıdır.
üzerinde ise bir teklik bağlantısıdır.
Dikey eşdeğişken diferansiyel
Verilen karma demet 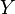 (1), burada
(1), burada 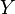 üzerinde vektör demetlerinin tam dizisi aşağıdadır:
üzerinde vektör demetlerinin tam dizisi aşağıdadır:
burada 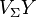 ve
ve 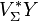
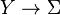 nın dikey tanjant demet ve dikey kotanjant demetidir.Her bağlantı bir lif demeti
nın dikey tanjant demet ve dikey kotanjant demetidir.Her bağlantı bir lif demeti 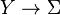 üzerinde
üzerinde 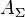 bölme verir
bölme verir
tam dizisinin (2). Bu bölme kullanılarak, bir birinci dereceden diferansiyel işlemcinin oluşturulabilmesi
bir karma demet 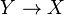 üzerinde. Buna dikey eşdeğişken diferansiyel denir.
üzerinde. Buna dikey eşdeğişken diferansiyel denir.
Bu şu önemli özelliği sahiptir.
Diyelimki ,
, 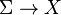 bir lif demetinin bir kesiti olsun, ve yine
bir lif demetinin bir kesiti olsun, ve yine 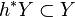 ,
,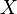 üzerinde geriçekme demeti olsun. Her
üzerinde geriçekme demeti olsun. Her 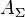 bağlantısı geriçekme bağlantısı uyarır
bağlantısı geriçekme bağlantısı uyarır
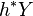 üzerinde ise
üzerinde ise 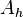 geri çekme bağlantısı ile ilişkili
geri çekme bağlantısı ile ilişkili 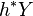 üzerinde yakın eşdeğişken diferansiyel
üzerinde yakın eşdeğişken diferansiyel 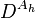 ile çakışan
ile çakışan 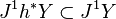 için bir
için bir 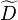 dikey eşdeğişken diferansiyelin sınırlarıdır .
dikey eşdeğişken diferansiyelin sınırlarıdır .
Kaynakça
- Saunders, D., The geometry of jet bundles. Cambridge University Press, 1989. ISBN 0-521-36948-7.
- Mangiarotti, L., Sardanashvily, G., Connections in Classical and Quantum Field Theory. World Scientific, 2000. ISBN 981-02-2013-8.
Diş bağlantılar
- Sardanashvily, G., Advanced Differential Geometry for Theoreticians. Fiber bundles, jet manifolds and Lagrangian theory, Lambert Academic Publishing, 2013. ISBN 978-3-659-37815-7; arXiv: 0908.1886
Ayrıca bakınız
- Bağlantı (matematik)
- Connection (fibred manifold)
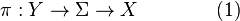

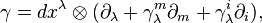
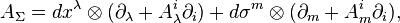
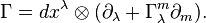
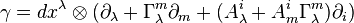
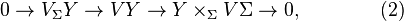
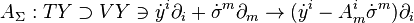
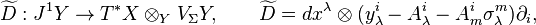
![A_h=dx^\lambda\otimes[\partial_\lambda+((A^i_m\circ h)\partial_\lambda h^m
+(A\circ h)^i_\lambda)\partial_i]](../I/m/05cfb37c7bb0c0276e02591bd452edf7.png)