Bağlantı (matematik)
Geometride bir bağlantı kavramı, paralel ve tutarlı bir şekilde bir eğri veya eğriler ailesi boyunca veri taşıma kesin fikri oluşturur.Modern geometrinin bağlantı türlerinin çeşitleri vardır,bir verinin ne türü bağlı olarak taşınmak isteniyor?Örneğin,en temel tip bir afin bağlantı,bir eğri boyunca bir noktadan bir manifolduna tanjant vektörlerin taşınması için bir araç verir. Belirli bir yönde bir vektör alanının sonsuz taşınması:Bir afin bağlantı tipik olarak vektör alanlarının yönlü türevlerinin alınması için bir vasıta sağlayan bir 'eşdeğişkin türev' şeklinde verilir.
Bunlar bir noktadaki yerel geometri ile başka bir noktadaki yerel geometri arasındaki bir karşılaştırmaya izin verir çünkü bağlantılar büyük ölçüde modern geometride merkezi bir önem taşımaktadır.
- Sonsuz ve yerel teorisi: diferansiyel geometri kendi içinde iki ana gruba ayrılır ve bağlantı tema'sı üzerinden çeşitli varyasyonları kucaklar. Öncelikle paralel taşınım ve holonomi kavramları ile yerel teoriyi ilgilendirir. Sonsuz teorisi ise geometrik verilerin farklılaşması ile ilgilenmektedir. Böylece esdegiskin türevin bir manifoldu başka bir vektör alanı boyunca bir vektör alanının bir türevini belirten bir yoldur.
- Bir Cartan bağlantısı diferansiyel formları ve Lie gruplarıni kullanarak bağlantı kuramının bazı varsayımlarını formüle etmenin bir yoludur.
- Bir Ehresmann bağlantısı fiber demeti veya alanın hareketinin izin verdiği yönü belirten bir temel demet içinde bir bağlantıdır.
- Bir Koszul bağlantısı bir vektör demeti (paketi) türevi genelleştirici bir bağlantıdır.
Bağlantılar ayrıca eğrilik (ayrıca eğrilik tensörü ve eğrilik formu ve burulma tensörü) gibi geometrik değişmezlerin uygun formülasyonlarına izin verir.
Alıştırma: koordinatların uygunsuzluğu
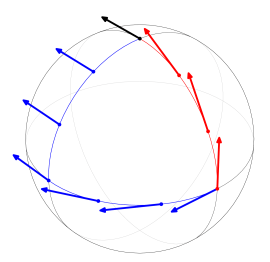
Paralel taşınım ın aracı olarak şu sorunu düşünün:Kuzey kutbunda S küresine bir tanjant vektör veriliyor, ve kürenin diğer noktalarına bu vektörü hareketli bir şekilde tanımlamış olduğunu varsayalım. Safça,uygun bakım uygulandığı sürece bu özel bir koordinat sistemi kullanılarak yapılabilir. Ancak, koordinatların bir sistemde tanımlı paralel taşınımı için başka bir koordinat sistemi kabul edilemez. Daha uygun bir paralel ulaşım için sistemi dönme altında kürenin simetrisini kullanmaktır.Kuzey kutbunda verilen bir vektör göz önüne alındığında, eksenel dönme olmadan kuzey kutbunda verilen bir eğri boyunca böyle bir şekilde kürenin dönmesi ile eğri boyunca hareket ederek bu vektör taşınabilir.Paralel taşınımın bu ikinci ve son aracı küre üzerinde Levi-Civita bağlantısıdır.İki farklı eğri aynı başlangıç ve bitiş noktasına sahiptir, ve bir v katı vektör bir dönme ile birinci eğri boyunca hareket ettirildiğinde, eğri terminal noktada elde edilen ikinci v katı vektör boyunca hareket eden vektörden farklı olacaktır. Bu olgu, kürenin eğriliğini gösterir. Paralel ulaşımı görselleştirmek için kullanılan basit bir mekanik cihaz güney-işaretleme arabasıdır.
Örneğin, S toparsal izdüşüm ile koordinatlar verildiğini varsayalım. S bakışıyla R3 içindeki birim vektörler oluşturuluyorsa S koordinatının yamaları bir çift taşır: kuzey kutbunun bir yakın komşuluğunda tek ve güney kutbunun diğer
Gönderimler:
sırasıyla kuzey kutbun U0 ve güney kutbunun U1 bir yakınkomşuluğunu kapsar. Diyelimki R3içinde X, Y, Z olsun ortam koordinatları olsun.Bunlar φ0 ve φ1 ise elimizde tersleri var
böylece koordinat geçiş fonksiyonu çember içinde tersidir:
Diyelimki şimdi biz bu koordinat türevleriyle ilişkili bileşenlerin terimleri içindeki bir vektör alanı gösteriyoruz. Eğer P U0 ⊂ Snin bir noktası,ise ilerletme ile bir vektör alanı gösterilebilir
burada ifadesi φ0nin Jacobiyen matrisini ifade eder, ve v0 = v0(x, y) R2 üzerinde bir vektör alanı v ile belirlenen tekliktir.Ötesi U0 ∩ U1 koordinat kartları arasında üst üste gelme üzerine, bu φ1 ya aynı vektör alanı sırasıyla göstermeye olası koordinatlardır:
v0 ve v1 bileşenlerinin bu ilişkisine φ1 = φ0 o φ01 zincir kuralı eşitliği uygulanır:
v1(φ1−1(P)) vektör bileşenlerine bu matris denkleminin iki tarafı uygulanır ve (1) ve (2) çağırılması elde edilen
Paralel bir eğri boyunca bir vektör alanını taşımak için nasıl tanımlanmasının ana sorusuna şimdi gelindi.Varsayalım şu P(t) S içinde bir eğridir.Naifçe, vektör alanının koordinat bileşenleri eğri boyunca sabit ise tek bir vektör alanı paralel düşünülebilir.Ancak, hemen bir belirsizlik ortaya çıkar: hangi koordinat sisteminin bu bileşenleri sabit olmalıdır?
Örneğin,bu varsayım v(P(t)) U1 koordinat sistemi içinde sabit bileşenler var.Bu fonksiyonlar v1(φ1−1(P(t))) sabittir.Bununla birlikte,çarpım kuralı (3)'e uygulanıyor ve kullanılıyor ,aslında d v1/dt = 0 verilen
Ama her zaman bir tekil-olmayan matristir (eğri bunu sağlar P(t) durgun değildir), böylece v1 ve v0 eşzamanlı sabit eğri boyunca hiç olamaz
Çözünürlük
Yukarıdaki problemde gözlenen vektör alanlarının bileşenlerine uygulandığında bu koordinat sistemi içinde değişiklik altında iyi davranmayan vektör hesabının kullanılan yönlü türevidir. Eğer bu gibi bir gösterim herhangi anlamda tüm yapılırsa bu onu paralel ötelemeli vektör alanlara oldukça zor tanıtabilir. Burada bu problemin çözümünün farklı iki temelli yolu var.
İlk yaklaşım incelemek içindir ve koordinat ötelemeleri altında yönlü türevin bir genellemesi için "iyi davranma" gereklidir.Bu bağlantılarına eşdeğişken türev yaklaşıklığı ile taktik almaktır:İyi davranış eşdeğişken ile eşittir. Burada belli bir doğrusal işlemci ile yönlü türevin tek bir modifikasyonu dikkate alınır,böyle bileşenlere Christoffel sembolü denir, bu kendi vektör alanları üzerinde türevler içermez. u yönü içinde bir φ koordinat sistemi içinde bir v vektörü bileşenlerinin Duv yön türevi bir eşdeğişken türev ile yerdeğiştirir:
burada φ koordinat sistem üzerinde bağımlı Γ,u ve v içinde çiftdoğrusaldır. Özel olarak, Γ u veya v üzerinde herhangi türevler içermez. Bu yaklaşımla öngörülen bir tavır içinde eğer φ koordinat sistemi farklı bir koordinat sistemiyle değiştirilirse dönüşüm Γ olmalı. Bu dönüşüm tensörel değildir, dolayısıyla bu içerik koordinat geçişinin yalnızca ilk türevi değildir, ama ayrıca bu ikinci türevdir. Γ'nın dönüşüm yasasını belirtme Γ teklik belirlemeye yeterli değildir. Bazı diğer normalizasyon durumları dayatılmalıdır, genellikle geometri altında düşünülen geometrinin tipi üzerinde bağlıdır. Riemannyen geometride, Levi-Civita bağlantısı Christoffel sembolleri ile metrikin bağdaştırılması gerekir (hem de belli bir simetri durumunda). Bu normalizasyonlar ile, bağlanan teklik (eşsizlik) olarak tanımlanıyor.
İkinci yaklaşım uzay üzerinde simetrinin bazı zerrelerini yakalamayı varsaymaya Lie grupları kullanmaktır. Bu Cartan bağlantı(sı)larının yaklaşımıdır.Örneğin yukarıda küre üzerinde vektörlerin özel paralel taşınıma dönmelerin kullanılması bu damar içinde pek çoktur.
Bağlantıların tarihi araştırması
Tarihsel olarak,bağlantılar Riemann geometrisinde bir sonsuz bakış açısıyla incelenmiştir.Bağlantıların sonsuz çalışması Christoffel ile bir ölçüde başladı.Bu daha sonra Gregorio Ricci-Curbastro ve Tullio Levi-Civita Levi-Civita & Ricci 1900 tarafından daha kapsamlı ele alındı. Christoffel'in sonsuz anlamında bir bağlantıda bir parça içinde Paralel taşınımın bir kavramı için ayrıca izin verdiği gözlendi Levi-Civita'nın sonraki çalışması diferansiyel denklemlerin çözümleri paralel yerdeğiştirmeler idi. Diferansiyel işlemcinin bir türü olarak bağlantıları konusunda odaklanmıştır. Yirminci yüzyıl ilerledikçe, Elie Cartan bağlantının yeni bir ifadesini geliştirdi. O Felix Klein'ın Erlangen programı geometrilerine Pfaffian sistemlerinin tekniklerini uygulamak için çalıştı.Eğrinin varlığı bağlantı ifadesi başka şekilde klasik bir Klein geometrinin sınırlarının izin verdiği müddetçe mevcut olacaktır : Bu araştırmalarda, o bağlantının belirli bir sonsuz küçük kavramının (bir Cartan bağlantı) bu geometrilere ve dahasına uygulanabilir olduğunu bulduk. ((Örneğin Cartan 1926 bak) ve (Cartan 1983).)(Örneğin Cartan 1926) ve Cartan 1983) Ayrıca Cartan Gaston Darboux kendi dinamiklerini kullanarak, sonsuz bağlantılar sınıfının paralel taşınım ifadesini yaygınlaştırmayı başardı. Bu bağlantının teorisi bir başka önemli kavram kurdu: böyle bir bağlantı diferansiyel form'un belli bir türüdür.
Bağlantı teorisinde iki konu günümüze kadar süregelmiştir: diferansiyel işlemci olarak bir bağlantı ve bir diferansiyel formun bir bağlantısı gibi. 1950 yılında, Jean -Louis Koszul Koszul 1950 Koszul bağlantısı vasıtasıyla bir diferansiyel işlemcinin bir bağlantısı ile ilgili bir cebirsel çerçeveyi verdi.Hem de Koszul bağlantısı Levi-Civita'nınkinden daha fazla genel oldu,ve nihayet ortadan kaldırmak için (ya da en azından gizlemek için) bağlantı formalizminden gelen garip Christoffel sembolleri ile sonuçlandırdı çünkü çalışmak daha kolay oldu.Eşlik eden paralel yerdeğiştirme operasyonlarında bağlantının terimleri içinde doğal cebirsel yorumlara vardı.
Etkin cebirsel kovaryant bir farklılaşma ve paralel öteleme arasında analitik yazışmayı dönüştürebilir başlangıç Koszul tanımı daha sonra, diferansiyel geometri topluluğunun çoğu tarafından kabul edildi.
Aynı yıl içinde, Charles Ehresmann Ehresmann 1950, Cartan'ın bir öğrencisi, ana demetin konuları içinde ve daha geneli, lif demeti bağlantısının üzerindeki bir diferansiyel form bağlantı üzerinde bir varyasyon sundu. Ehresmann bağlantılarının kesinlikle Cartan bağlantılarının bir genellemesi olmadığı konuşuluyordu. Cartan bağlantıları oldukça katı çünkü Cartan denklik yöntemi ile ilişkilerin manifoldunun temel diferansiyel topolojisi altında oldukça sıkı bir şekilde bağlı idi. Ehresmann bağlantıları yerine zaten böyle gösterge bağlantıları denebilecek çalışmaya uzak Cartan bağlantılarından harekete geçilmişti. Arasında Shiing-Shen Chern, gibi dönemin diğer geometricilerin temel çalışmalarını izlemek için sağlam bir çerçeve vardı. Bakış Ehresmann noktasında, bir ana demet içinde bir bağlantı demetinin toplam uzay üzerinde yatay ve dikey vektör alanlarının bir belirtimini oluşturmaktadır. Paralel ötelemenin ardından yatay ana demet bir eğriye tabanından bir eğrinin bir kaldırıcısıdır. Bu bakış açısının holonomi ile ilgili çalışmalarda özellikle değerli olduğu kanıtlanmıştır.
Olası yaklaşımlar
- Oldukça doğrudan bir yaklaşım, modülünün bir ögesi üzerinde bir eşdeğişken türev hareketi bir diferansiyel işlemci olarak vektör alan(ı)larının nasıl olduğunu belirtmek içindir. Daha genel,herhangi vektör demeti içinde bağlantılar için uygulanan bir benzer yaklaşımdır.
- Geleneksel indis gösteriminin bileşenler ile bağlantısı özeldir; bakınız Christoffel sembolleri. (Not: bu üç indisler var, ama bir tensör değildir).
- Yalancı-Riemannyen'de ve Riemannyen geometri Levi-Civita bağlantı bir özel bağlantı metrik tensöre ilişkilidir.
- Bu afin bağlantının bir örneğidir.Burada ayrıca bir izdüşümsel bağlantı kavramı,karmaşık analiz içinde Schwarzyen türeve bir örnektir.Daha doğrusu, hem afin ve hem izdüşümsel bağlantılar Cartan bağlantılarının tipidir.
- Temel demetler kullanılıyor, bir bağlantı bir Lie cebri-değeri diferansiyel form olarak gerçekleştirilebilir.Bakınız bağlantı (temel demet).
- Bir bağlantıya yaklaşım bu "veri"nin taşınımının gösteriminin direk kullanımı (her ne olursa) Ehresmann bağlantısı yapar.
- Daha soyut bir yaklaşımı belki Alexander Grothendieck önerdi, burada bir Grothendieck bağlantısı iniş köşegenin sonsuz yakınlığından veri olarak görülüyor; bkz Osserman 2004.
Kaynakça
- Levi-Civita, T.; Ricci, G. (1900), "Méthodes de calcul différential absolu et leurs applications", Math. Ann. B 54: 125–201, DOI:10.1007/BF01454201
- Cartan, Élie (1924), "Sur les varietes a connexion projective", Bulletin de la Société Mathématique 52: 205–241
- Cartan, Élie (1926), "Espaces à connexion affine, projective et conforme", Acta Math. 48: 1–42, DOI:10.1007/BF02629755
- Cartan, Élie (1983), Geometry of Riemannian spaces, Math Sci Press, ISBN 978-0-915692-34-7, http://books.google.com/?id=-YvvVfQ7xz4C&printsec=frontcover
- Ehresmann, C. (1950), Les connexions infinitésimales dans un espace fibré différentiable, Colloque de Toplogie, Bruxelles, ss. 29–55
- Koszul, J. L. (1950), "Homologie et cohomologie des algebres de Lie", Bulletin de la Société Mathématique 78: 65–127
- Lumiste, Ü. (2001), "Connection", Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104, http://eom.springer.de/C/c025140.htm
- Osserman, B. (2004) (PDF), Connections, curvature, and p-curvature, http://math.berkeley.edu/~osserman/math/connections.pdf
- Mangiarotti, L.; Sardanashvily, G. (2000), Connections in Classical and Quantum Field Theory, World Scientific, ISBN 981-02-2013-8.
- Morita, Shigeyuki (2001), Geometry of Differential Forms, AMS, ISBN 0-8218-1045-6
Dış bağlantılar
- Connections at the Manifold Atlas
Ayrıca bakınız
- Afin bağlantı
- Cartan bağlantısı
- Ehresmann bağlantısı
- Bağlantı(lifli manifold)
- Bağlantı (ana demet)
- Bağlantı (vektör demeti)
- Bağlantı(afin demet)
- Bağlantı(karma demet)
- Bağlantı (cebrik çerçeve)