Holonomi

Bir küre üzerindeki yol üzerinde paralel taşıma. A → N → B → A dan taşımayla başlangıç vektörden farklı formlardaki bir vektör elde edilir. Bu başlangıç vektöre dönmedeki hata bağlantının holonomisi ile ölçülür.

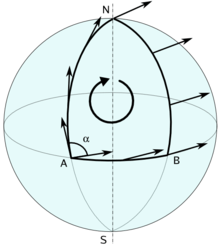
Diferansiyel geometride, bir düzgün manifold üzerinde bir bağlantının holonomisi paralel taşınım döngüleri geometrik verilerini taşırken korumak için başarısız kapalı döngüler ölçüm bağlantı uzantılarının eğriliğinin genel geometrik sonucudur. Düzgün bağlantılar için, ilişkili holonomi monodromi türüdür, ve doğal olarak küresel bir kavramdır. Eğrilik bağlantılar için, holonomi nontrivial yerel ve küresel özelliklere sahiptir.

Bir manifold üzerinde herhangi bir tür holonominin bazı kavramlarına, paralel taşınım göndermeler aracılığıyla bağlantılıdır. Holonominin en yaygın formları simetrinin bazı tür bağlantıları için bulunmaktadır. Önemli örnekleri arasında aşağıdakiler bulunmaktadır: (Riemannyen holonomi adlandırılır) Riemannyen geometride Levi-Civita bağlantısının holonomisi, vektör demetleri içinde bağlantılarının holonomisi, Cartan bağlantılarının holonomisi ve temel demetlerin (ana demet) bağlantılarının holonomisi. Bu durumların her birinde, bağlantıların holonomisi bir Lie grubu holonomi grubu ile ayırtedilebilir.Ambrose–Singer teoremi yoluyla bir bağlantının holonomisi bağlantının eğriliği ile yakından ilişkilidir.

Riemannyen holonomi çalışması önemli bir dizi gelişmelere yol açmıştır. Holonomi simetrik uzayları incelemek ve sınıflandırmak amacıyla Cartan (1926 ) tarafından tanıtıldı. Bu daha sonra ki holonomi grupları daha genel bir çerçevede Riemann geometrisi çalışmaları için kullanılacak kadar değildi. 1952 yılında Georges de Rham de Rham ayrıştırma teoremi, yerel holonomi gruplarının etkisi altında indirgenemez uzay içine tanjant demeti ile bölerek Riemann manifoldlarının bir Kartezyen çarpımı içine bir Riemann manifoldu parçalamak için bir ilke kanıtladı. Daha sonra, 1953 yılında, M. Berger mümkün indirgenemez holonomileri sınıflandırdı. Riemann holonomi ayrıştımasının ve sınıflandırmasının ve özelliklede sicim teorisi için fizik uygulamaları vardır.

Bir vektör demeti içinde bir bağlatının holonomisi

Diyelimki E bir düzgün manifold M üzerinde bir k dereceli vektör demeti ve diyelimki ∇ E üzerinde bir bağlantı olsun. Verilen bir parçalı düzgün döngü M içinde x tan temelli γ : [0,1] → M,bağlantı bir paralel taşınım göndermesi P_γ: E_x → E_x tanımlar. Bu gönderme hem doğrusal ve tersinebilir ve hem de GL(E_x) nin bir ögesi gibi tanımlanır .x da temelli ∇'nın Holonomi grubu olarak tanımı şöyledir

${\displaystyle \mathrm {Hol} _{x}(\nabla )=\{P_{\gamma }\in \mathrm {GL} (E_{x})\mid \gamma {\text{ döngüsünün temeli }}x\}.}$'tır

x da tabanlı sınırlı holonomi grubu γ döngüleri kasılabilirlikten gelen ${\displaystyle \mathrm {Hol} _{x}^{0}(\nabla )}$ altgruplarıdır.

Eğer M taban noktası x üzerinde holonomi grubu bağlantıları ise bağlantı yalnızca birleşmeGL(k, R) kadar içindedir. açıkça, eğer bir γ yolu M içinde x dan y ye ise

${\displaystyle \mathrm {Hol} _{y}(\nabla )=P_{\gamma }\mathrm {Hol} _{x}(\nabla )P_{\gamma }^{-1}.}$

E_x ile R^k nin seçilen farklı ayrıştırımı ayrıca birleşme altgrupları verir. Bazen,genel içinde özel veya resmi olmayan tartışmalar (aşağıdaki gibi), bir tanım birleşimi kadar iyi olduğu anlayışı ile, temel noktaya başvuru yapabilir

Holonomi grubu dahilinde bazı önemli özellikler:

• Hol⁰(∇) bir bağlantı ve GL(k, R) nin Lie altgrubudur.
• Hol⁰(∇) Hol(∇) nin etkisiz bileşenidir.
• Burada bir doğal, örten grup homomorfizmi π₁(M) → Hol(∇)/Hol⁰(∇),π₁(M) burada M in temel grubudur, bu P_γ·Hol⁰(∇)eşküme'ye homotopi sınıfı [γ] gönderir.
• Eğer M basit bağlantı ise Hol(∇) = Hol⁰(∇).
• ∇ düzgündür (yani eğrilik yoktur) ancak ve ancak Hol⁰(∇) önemsizdir.

Bir ana demet içinde bir bağlantının holonomisi

Paralel şekilde ana demet kazancı üzerinde bağlantının holonomisi için tanımlanır.G bir düzgün manifold M üzerinde bir Lie grubu ve P bir ana G-demet ise bu parakompakttır. ω P üzerinde bir bağlantı olsun.M içinde x da temelli γ : [0,1] → M bir parça düzgün döngü veriliyor x üzerinde lif içinde bir p noktası,bağlantı ${\displaystyle {\tilde {\gamma }}(0)=p}$ gibi benzersiz bir ${\displaystyle {\tilde {\gamma }}\colon [0,1]\to P}$ yatay kayma tanımlar.Yatay kaymanın son noktası, ${\displaystyle {\tilde {\gamma }}(1)}$,p ama x üzerinde lif içinde p·g içinde bazı diğer noktalara rağmen genel olacak değildir :p ~ q diyerek bu P üzerinde tanımlanan bir eşdeğer ilişki ise ~P içinde yatay yolun bir parçası ile birleştirilebilir.

p de temelli ω'nın holonomi grup ise tanım olarak

${\displaystyle \mathrm {Hol} _{p}(\omega )=\{g\in G\mid p\sim p\cdot g\}.\,}$

p de temelli sınırlı holonomi grup γ döngüsü kasılabilirin döngüsü yatay kaymalardan gelen Hol⁰_p(ω) altgrubudur.

Eğer M ve P bağlantılı ise sadece G içinde birleşme kadar taban noktası p üzerinde bağlı holonomi grubudur.Açıkça, eğer q holonomi grubuna sahip herhangi bir başka seçilmiş ana nokta, ise q ~ p g gibi burada bir g ∈ G eşsizlik var .gnin bu değeri ile,

${\displaystyle \mathrm {Hol} _{q}(\omega )=g^{-1}\mathrm {Hol} _{p}(\omega )g.\,}$

Özel olarak,

${\displaystyle \mathrm {Hol} _{p\cdot g}(\omega )=g^{-1}\mathrm {Hol} _{p}(\omega )g,}$

Dahası, eğer p ~ q ise Hol_p(ω) = Hol_q(ω). Yukarıda olduğu gibi, bazen bir tanım konjugasyon kadar iyi olduğu anlayışı ile, holonomi grubunun ana noktasına başvuru yapar

holonomin bazı önemli özellikleri ve sınırlı holonomi grupları içerenler:

• Hol⁰_p(ω) Gnin bir Lie altgrupları bağlantısıdır.
• Hol⁰_p(ω) , Hol_p(ω)'nin etkisiz bileşenidir.
• Burada bir örten grup homomorfizmi π₁(M) → Hol_p(ω)/Hol⁰_p(ω) doğaldır.
• Eğer M basit bağlantılı ise Hol_p(ω) = Hol⁰_p(ω).
• ω düzgün (yani eğrilik kaybı var) ancak ve ancak Hol⁰_p(ω) önemsizdir.

Notlar

Kaynakça

• Agricola, Ilka (2006), "The Srni lectures on non-integrable geometries with torsion", Arch. Math 42: 5–84 
• Ambrose, W.; Singer, I. M. (1953), "A theorem on holonomy", Trans. Amer. Math. Soc. (American Mathematical Society) 75 (3): 428–443, DOI:10.2307/1990721, JSTOR 1990721 
• Baum, H.; Friedrich, Th.; Grunewald, R.; Kath, I. (1991), Twistors and Killing spinors on Riemannian manifolds, B.G. Teubner 
• Berger, M. (1953), "Sur les groupes d'holonomie homogènes des variétés a connexion affines et des variétés riemanniennes", Bull. Soc. Math. France 83: 279–330, MR 0079806, http://www.numdam.org/numdam-bin/fitem?id=BSMF_1955__83__279_0 
• Besse, Arthur L. (1987), Einstein manifolds, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 10, Berlin, New York: Springer-Verlag, ss. xii+510, ISBN 978-3-540-15279-8 
• Bonan, Edmond (1965), "Structure presque quaternale sur une variété différentiable", C. R. Acad. Sci. Paris 261: 5445–5448 .
• Bonan, Edmond (1966), "Sur les variétés riemanniennes à groupe d'holonomie G2 ou Spin(7)", C. R. Acad. Sci. Paris 320: 127–129 ].
• Borel, Armand; Lichnerowicz, André (1952), "Groupes d'holonomie des variétés riemanniennes", Les Comptes rendus de l'Académie des sciences 234: 1835–1837, MR 0048133 
• Bryant, Robert L. (1987), "Metrics with exceptional holonomy", Annals of Mathematics (Annals of Mathematics) 126 (3): 525–576, DOI:10.2307/1971360, JSTOR 1971360 .
• Bryant, Robert L. (1991), "Two exotic holonomies in dimension four, path geometries, and twistor theory", Amer. Math. Soc. Proc. Symp. Pure Math. 53: 33–88 
• Bryant, Robert L. (2000), "Recent Advances in the Theory of Holonomy", Asterisque, Séminaire Bourbaki 1998–1999 266: 351–374  arXiv:math.DG/9910059.
• Cartan, Élie (1926), "Sur une classe remarquable d'espaces de Riemann", Bulletin de la Société Mathématique de France 54: 214–264, ISSN 0037-9484, MR 1504900 
• Cartan, Élie (1927), "Sur une classe remarquable d'espaces de Riemann", Bulletin de la Société Mathématique de France 55: 114–134, ISSN 0037-9484 
• Chi, Quo-Shin; Merkulov, Sergey A.; Schwachhöfer, Lorenz J. (1996), "On the Incompleteness of Berger's List of Holonomy Representations", Invent. Math. 126: 391–411  arXiv:dg-da/9508014.
• Joyce, D. (2000), Compact Manifolds with Special Holonomy, Oxford University Press, ISBN 0-19-850601-5 
• Kobayashi, S.; Nomizu, K. (1963), Foundations of Differential Geometry, Vol. 1 & 2, Wiley-Interscience (yayın: 1996 New edition), ISBN 0-471-15733-3 
• Kraines, Vivian Yoh (1965), "Topology of quaternionic manifolds", Bull. Amer. Math. Soc 71,3, 1: 526–527 .
• Lawson, H. B.; Michelsohn, M-L. (1989), Spin Geometry, Princeton University Press, ISBN 0-691-08542-0 
• Merkulov, Sergei A.; Schwachhöfer, Lorenz J. (1999), "Classification of irreducible holonomies of torsion-free affine connections", Ann. Of Math. (Annals of Mathematics) 150 (1): 77–149, DOI:10.2307/121098, JSTOR 121098  arXiv:math.DG/9907206; "Addendum", Ann. Of Math. 150 (3): 1177–1179, 1999, DOI:10.2307/121067, JSTOR 121067.  arXiv:math.DG/9911266.
• Olmos, C. (2005), "A geometric proof of the Berger Holonomy Theorem", Annals of Mathematics 161 (1): 579–588, DOI:10.4007/annals.2005.161.579, http://annals.math.princeton.edu/2005/161-1/p11 
• Sharpe, R.W. (1997), Differential Geometry: Cartan's Generalization of Klein's Erlangen Program, Springer-Verlag, New York, ISBN 0-387-94732-9 
• Schwachhöfer, Lorenz J. (2001), "Connections with irreducible holonomy representations", Advances in Mathematics 160 (1): 1–80, DOI:10.1006/aima.2000.1973 
• Simons, J. (1962), "On the transitivity of holonomy systems", Annals of Mathematics (Annals of Mathematics) 76 (2): 213–234, DOI:10.2307/1970273, JSTOR 1970273 
• Spivak, M. (1999), A comprehensive introduction to differential geometry, Volume II, Houston, Texas: Publish or Perish, ISBN 0-914098-71-3 
• Sternberg, S. (1964), Lectures on differential geometry, New York: Chelsea, ISBN 0-8284-0316-3 
• Golwala, S. (2007), Lecture Notes on Classical Mechanics for Physics 106ab, http://www.astro.caltech.edu/~golwala/ph106ab/ph106ab_notes.pdf 
• Markushevich, A.I.; Silverman, Richard A. (ed.) (2005) [1977], Theory of functions of a Complex Variable (2nd bas.), New York: American Mathematical Society, ss. 112, ISBN 0-8218-3780-X, http://books.google.com/?id=H8xfPRhTOcEC&dq 

Daha fazla bilgi

• Literature about manifolds of special holonomy, a bibliography by Frederik Witt.