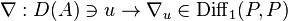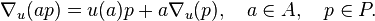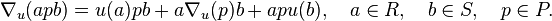Bağlantı (cebrik çerçeve)
Kuantum sistemlerinin geometrisi (yani değişmeli olmayan geometri ve süpergeometri) başlıcasıdır
modülü'nün cebrik terimleri içinde ifade edilir ve cebirin bağlantılar modülü üzerine 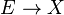 'nin kesitlerinin
'nin kesitlerinin 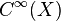 -modülü üzerinde bir Koszul bağlantısı üzerinde olarak yazılan bir düzgün vektör demeti bir doğrusal bağlantısının genellemesidir
-modülü üzerinde bir Koszul bağlantısı üzerinde olarak yazılan bir düzgün vektör demeti bir doğrusal bağlantısının genellemesidir 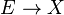 [1]
[1]
Değişmeli cebir
Diyelimki  bir değişmeli halka olsun ve
bir değişmeli halka olsun ve 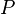 bir
bir  -modül.Burada
-modül.Burada 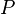 üzerinde bir bağlantının farklı eşitlik tanımlarıdır.[2] Diyelimki
üzerinde bir bağlantının farklı eşitlik tanımlarıdır.[2] Diyelimki 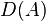 ,
,  halkasının türevlerinin modülü olsun.Bir
halkasının türevlerinin modülü olsun.Bir
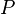 üzerinde bir
üzerinde bir  -modulü bağlantı tanımlanıyor bir
-modulü bağlantı tanımlanıyor bir  -modül biçimi olarak
-modül biçimi olarak
böylece ilk sıra diferensiyel işlemciler 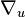
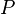 üzerinde Leibniz kuralı uyar
üzerinde Leibniz kuralı uyar
Değişmeli halka üzerinde bir modül bağlantıları her zaman var.
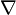 bağlantısının eğriliği sıfır-sıralı differensiyel işlemci olarak tanımlanıyor
bağlantısının eğriliği sıfır-sıralı differensiyel işlemci olarak tanımlanıyor
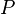 modülü üzerinde tüm
modülü üzerinde tüm 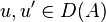 için
için ![R(u,u')=[\nabla_u,\nabla_{u'}]-\nabla_{[u,u']} \,](../I/m/5df22730aca9a10eacce8a9a01dcb8b6.png)
Eğer 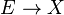 bir vektör demeti ve burada bir-e-birdir
doğrusal bağlantılar arasında karşılık gelen
bir vektör demeti ve burada bir-e-birdir
doğrusal bağlantılar arasında karşılık gelen 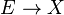 üzerinde
üzerinde 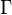 ve
ve
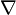 üzerinde bağlantılar
üzerinde bağlantılar
Açıkçası 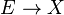 üzerinde bir bağlantının eşdeğişken diferansiyeline karşı
üzerinde bir bağlantının eşdeğişken diferansiyeline karşı 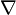
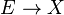 nin kesitlerinin
nin kesitlerinin 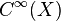 -modülüdür .
-modülüdür .
Değişmeli cebir dereceleri
Değişmeli halkalar üzerinde modül üzerinde bir bağlantının gösterimi is bir dereceli değişmeli cebir üzerinde modüle doğrudan doğruya uzanır.[3] Bu dereceli manifoldlar ve supervektör demetlerinin supergeometrisi içinde superbağlantılarının durumudur. Superbağlantı her zaman var.
Geçişsiz cebir
Eğer  bir değişmeli olmayan halka,
bir değişmeli olmayan halka, -modülü soldaki ve sağdaki bağlantıları
değişmeli halkaları üzerinde modüllerinde kişilerce benzer bir şekilde tanımlanır.[4] Ancak bu bağlantıların varlığı gerekmez.
-modülü soldaki ve sağdaki bağlantıları
değişmeli halkaları üzerinde modüllerinde kişilerce benzer bir şekilde tanımlanır.[4] Ancak bu bağlantıların varlığı gerekmez.
Sağ ve sol modülleri üzerindeki bağlantıların aksine, bir üzerine bir bağlantı tanımlamak konusunda bir sorun var
değişmeli olmayan halkalar üzerinde 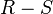 -çiftmodül
-çiftmodül
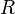 ve
ve 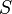 . Burada farklı tanımlamalar
gibi bir bağlantının.[5] Diyelimki onların bir anlamı.Bir
. Burada farklı tanımlamalar
gibi bir bağlantının.[5] Diyelimki onların bir anlamı.Bir
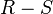 -bimodule
-bimodule 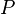 üzerinde bir bağlantı bir çiftmodül
biçimi olarak tanımlanıyor
üzerinde bir bağlantı bir çiftmodül
biçimi olarak tanımlanıyor
Buna uyan Leibniz kuralı
Ayrıca bakınız
- Bağlantı (vektör demeti)
- Bağlantı (matematik)
- Geçişli olmayan geometri
- Supergeometri
- Değişmeli cebir üzerinde diferansiyel
Notlar
Kaynakça
- Koszul, J., Homologie et cohomologie des algèbres de Lie, Bulletin de la Société Mathématique 78 (1950) 65
- Koszul, J., Lectures on Fibre Bundles and Differential Geometry (Tata University, Bombay, 1960)
- Bartocci, C., Bruzzo, U., Hernandez Ruiperez, D., The Geometry of Supermanifolds (Kluwer Academic Publ., 1991) ISBN 0-7923-1440-9
- Dubois-Violette, M., Michor, P., Connections on central bimodules in noncommutative differential geometry, J. Geom. Phys. 20 (1996) 218. arXiv:q-alg/9503020v2
- Landi, G., An Introduction to Noncommutative Spaces and their Geometries, Lect. Notes Physics, New series m: Monographs, 51 (Springer, 1997) ArXiv eprint, iv+181 pages.
- Mangiarotti, L., Sardanashvily, G., Connections in Classical and Quantum Field Theory (World Scientific, 2000) ISBN 981-02-2013-8
Dış bağlantılar
- Sardanashvily, G., Lectures on Differential Geometry of Modules and Rings (Lambert Academic Publishing, Saarbrücken, 2012); arXiv: 0910.1515