Diferansiyel dereceli Lie cebri
Cebirde,bir diferansiyel dereceli Lie cebiri veya dg Lie cebiri, bir dereceli vektör uzayı "sıfır karakteristiği" ile birlikte 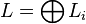 bir alanı üzerinde bir doğrusal harita
bir alanı üzerinde bir doğrusal harita ![[,]: L_i \otimes L_j \to L_{i+j}](../I/m/b93d2ab239a5f6549e8403d9d54b7607.png) ve bir diferansiyeldir
ve bir diferansiyeldir
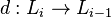 ifadesi doyurucudur.
ifadesi doyurucudur.
Jacobi özdeşliği ile derece
Leibniz kuralı ile derece:
x, y ve z gibi L içindeki herhangi bir öge için
Ana uygulama "sıfır karakteristiği"nde deformasyon teorisidir (özel olarak karmaşık sayılar üzerinde.) Bu fikir için Quillen'in üzerinde çalıştığı Rasyonel homotopi teorisi'ne bakmak gerekir.Bu tezi formüle etmenin bir yolu olabilir (due to Drinfeld, Feigin, Deligne, Kontsevich, et al.):[1] Karakteristik sıfır problemi içindeki herhangi bir makul resmi deformasyon sorunu,Lie cebrinin uygun bir dg Maurer-Cartan elemanları tarafından tarif edilebilir.
Ayrıca bakınız
- Diferansiyel dereceli Lie cebri (DGA)
Kaynakça
- ↑ Hinich, DG coalgebras as formal stacks arXiv:math/9812034
- Daniel Quillen, Rational Homotopy Theory
Daha ileri okuma
- J. Lurie, Formal moduli problems, section 2.1
Dış bağlantılar
- Şablon:Nlab
- Şablon:Nlab
Şablon:Algebra-stub
![[x,y] = (-1)^{|x||y|+1}[y,x],](../I/m/d15e5728fef6a1c6339281f18eac4b85.png)
![(-1)^{|x||z|}[x,[y,z]] +(-1)^{|y||x|}[y,[z,x]] +(-1)^{|z||y|}[z,[x,y]] = 0,](../I/m/feb68c275a45c5610f3db53c9efbf2ba.png)
![d [x,y] = [d x,y] + (-1)^{|x|}[x, d y]](../I/m/ac7877c34aad794614b4a84426b5207e.png)