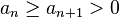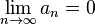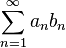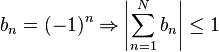Dirichlet testi
Matematikte Dirichlet testi, bir serinin yakınsaklığını belirlemek için kullanılan bir yöntemdir ve matematikçi Johann Dirichlet'nin arkasından isimlendirilmiştir.
Gerçel sayıların iki dizisi, 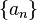 ve
ve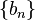 , verilsin. Bu diziler, M bir sabit iken aşağıdakileri sağlıyorsa
, verilsin. Bu diziler, M bir sabit iken aşağıdakileri sağlıyorsa
- her N pozitif tamsayısı için
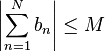
- her N pozitif tamsayısı için
o zaman
serisi yakınsar.
Dirichlet testinin bir sonucu
durumunda daha genel bir kullanımı olan almaşık seri testidir.
Bir diğer sonuç ise 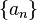 'nin sıfıra giden azalan bir dizi olduğu her zaman
'nin sıfıra giden azalan bir dizi olduğu her zaman 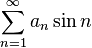 serisinin yakınsamasıdır.
serisinin yakınsamasıdır.
Kaynakça
- Hardy, G. H., A Course of Pure Mathematics, Ninth edition, Cambridge University Press, 1946. (sf. 379-380).
- Voxman, William L., Advanced Calculus: An Introduction to Modern Analysis, Marcel Dekker, Inc., New York, 1981. (§8.B.13-15) ISBN 0-8247-6949-X.
Dış bağlantılar
This article is issued from Vikipedi - version of the 2/15/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.