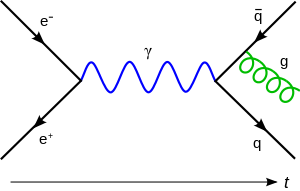
Feynman diyagramları

Bu Feynman diyagramında, bir elektron ve bir pozitron yokoluşu, bir foton'un üretilmesi ( mavi sine dalgası tarafından gösterilebilir) alıyor bir kuark-antikuark çifti, sonrasında antiquark ışıması bir gluon (yeşil helis ile gösterilebilir).

Teorik fizikte Feynman diagramları bir Feynman diyagramının davranışını düzenleyen matematiksel ifadelerin resimsel sunumlar katılarak diyagram tarafından açıklandığı gibi atomaltı parçacıklarların davranışları gösterilmiştir.Bu şemalar bunları bulan adınadır, Amerikan fizikçisi Richard FeynmanNobel Ödülü-kazandı , ve 1948 yılında tanıttı. Atomaltı parçacıkların ilişkileri sezgisel anlamak karışık ve zor olabilir , ve Feynman diagramları oldukça gizemli soyut formülün basit bir gösterimine izin verir.David Kaiser yazdıki, "yüzyılın ortasından bu yana, bu diagramlar teorik fizikçiler için giderek zorlaşan kritik hesaplamalar uygulamasına yardım araçlarıdır," ve "Feynman diagramları Teorik fizikte her yönüyle neredeyse devrimdir.".^[1] kuantum alan teorisi diyagramların ilk uygulamasıdır, ayrıca ,katı-hal teorisi gibi diğer alanlardada kullanılabilir.

Feynman Zamanda bir elektronun hareketi geriye doğru imiş gibi bir pozitron yorumu önerdi.^[2] ve böylece antiparçacıklar Feynman diyagramları ile hem uzay eksenli ve hem de bir zaman eksenli ama zaman içinde geriye doğru uzayda ileriye doğru hareket eden parçacıklar olarak yorumlanır. Teorik parçacıklar fiziği için olasılık genliği hesaplamaları gereklidir ve çok sayıda değişken üzerinde büyük kesirler ve karışık integraller kullanılabilir . Bunula birlikte düzgün bir yapıda bu integraller belkide grafik gösterimle Feynman diyagramları ile olabilir. Bir Feynman diagramı bir parçacık yolunun bir parçacık sınıfının bir katkısıdır,bu katkı ve şemada tanımlanarak bölünmüş. Daha kesin bir ifadeyle, ve teknik olarak, Bir Feynman diyagramı geçiş genliği bir pertürbatif katkının bir grafik temsilidir veya bir kuantum mekaniksel veya istatistiksel alan teorisinin korelasyon fonksiyonudur. Bununla birlikte kuantum alan teorisinin kanonik formülasyonunda,bir Feynman diyagramında perturbative içindeki terimler S-matrixi ile Wick's açılımını temsil eder .Alternatif olarak,yol integrali formulasyonu kuantum alan teorisinin geçiş genliği sistem sınırından son duruma kadar parçacıklar veya alanlar içindeki terimler bütün olası geçmişlerin bir ağırlık toplamının gösterimidir.burada geçiş genliği sınırlar arası bir S-matrix matris elemanı ile verilir ve bu kuantum sistemin son durumudur.

Kanonik nicemleme formülasyonu

Olasılık genliği başlangıç durumu bir kuantum sisteminin bir geçişi için ${\displaystyle |i\rangle }$ son durumuna matris elemanı

${\displaystyle |f\rangle }$ tarafından verilir.

${\displaystyle S_{fi}=\langle f|S|i\rangle \;,}$

burada ${\displaystyle S}$ S-matris'tir. kanonik kuantum alan teorisinde etkileşim resmi Lagrangian etkileşimin kuvveti bir pertürbasyon serisi tarafından S-matris ile gösterilir.

${\displaystyle S=\sum _{n=0}^{\infty }{i^{n} \over n!}\int \prod _{j=1}^{n}d^{4}x_{j}T\prod _{j=1}^{n}L_{v}(x_{j})\equiv \sum _{n=0}^{\infty }S^{(n)}\;,}$

burada ${\displaystyle L_{v}}$ Lagrangian etkileşimdir ve ${\displaystyle T}$ operatörler zaman sıralı ürün anlamına gelir.

${\displaystyle T\prod _{j=1}^{n}L_{v}(x_{j})=\sum _{\mathrm {all\;possible\;contractions} }(\pm )N\prod _{j=1}^{n}L_{v}(x_{j})\;,}$

burada $N$ operatörler normal ürün anlamına gelir ve${\displaystyle (\pm )}$ olası işaret değişikliği fermiyonik operatörlerin gidip gelmesi için bir büzülme(biryayıcı) bir araya getirmekle ilgilenir

Feynman kuralları

Diyagramlar etkileşimi Lagrange bağlıdır ve Feynman kurallarına göre çizilir. Lagrangian etkileşimi için QED , ${\displaystyle L_{v}=-g{\bar {\psi }}\gamma ^{\mu }\psi A_{\mu }}$,Bir fermiyonik alanının etkileşimini tarif etmektedir.${\displaystyle \psi }$ Bir bozonik gauge alanı ile ${\displaystyle A_{\mu }}$, Feynman kuralları aşağıdaki koordinat uzayında formüle edilebilir:

1. Her entegrasyonu koordine${\displaystyle x_{j}}$ bir nokta tarafından gösteriliyor (bazen tepe denir);
2. bozonik bir yayıcı iki noktayı birleştiren bir salınan çizgi ile temsil edilir;
3. fermiyonik bir propagator iki noktayı birleştiren bir düz çizgi ile temsil edilir;
4. bozonik bir alan ${\displaystyle A_{\mu }(x_{i})}$ noktasına bağlanmış bir salınan çizgiyle temsil edilr $x_i$;
5. fermiyonik bir alan ${\displaystyle \psi (x_{i})}$ noktaya bağlı düz bir çizgi ile temsil $x_i$ noktasına doğru bir ok ile;
6. fermionik bir alan ${\displaystyle {\bar {\psi }}(x_{i})}$ noktaya bağlı düz bir çizgi $x_i$ ;

Örnek: QED ikinci derece süreçler

S-matris içinde ikinci dereceden pertürbasyon terimidir

${\displaystyle S^{(2)}={(ie)^{2} \over 2!}\int d^{4}x\,d^{4}x'\,T{\bar {\psi }}(x)\,\gamma ^{\mu }\,\psi (x)\,A_{\mu }(x)\,{\bar {\psi }}(x')\,\gamma ^{\nu }\,\psi (x')\,A_{\nu }(x').\;}$

Fermiyonların saçılması

Integrandı verilen Wick's açılımı (diğerleri boyunca) aşağıdaki terimler ${\displaystyle N{\bar {\psi }}(x)\gamma ^{\mu }\psi (x){\bar {\psi }}(x')\gamma ^{\nu }\psi (x'){\underline {A_{\mu }(x)A_{\nu }(x')}}\;,}$

burada ${\displaystyle {\underline {A_{\mu }(x)A_{\nu }(x')}}=\int {d^{4}k \over (2\pi )^{4}}{-ig_{\mu \nu } \over k^{2}+i0}e^{-ik(x-x')}}$

Feynman gauge içindeki elektromanyetik büzüşmedir (yayıcı). Bu terimler sağda Feynman diyagramı tarafından gösteriliyor büzülme diyagramı verilmiştir. sağdaki:

1. ${\displaystyle e^{-}e^{-}}$ saçılma (sağdski sınır durum, son durum diyagramın solu);
2. ${\displaystyle e^{+}e^{+}}$ saçılma (soldakisınır durum, son durum diyagramın sağı);
3. ${\displaystyle e^{-}e^{+}}$ saçılma (alttaki sınır durum/üst, son durum diyagramda üst/alt ).

Compton saçılması ve and imha${\displaystyle e^{-}e^{+}}$çiftini üretme

açılımdaki diğer önemli bir terim

${\displaystyle N{\bar {\psi }}(x)\,\gamma ^{\mu }\,{\underline {\psi (x)\,{\bar {\psi }}(x')}}\,\gamma ^{\nu }\,\psi (x')\,A_{\mu }(x)\,A_{\nu }(x')\;,}$

burada

${\displaystyle {\underline {\psi (x){\bar {\psi }}(x')}}=\int {d^{4}p \over (2\pi )^{4}}{i \over \gamma p-m+i0}e^{-ip(x-x')}}$

fermiyonik büzülmedir (propagator).

Elektron-pozitron imha örnekleri

Elektron-Pozitron imhasında Feynman Diagramı

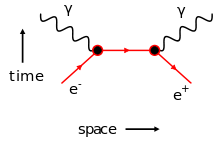
The elektron-pozitron imha etkileşimi:

${\displaystyle e^{+}e^{-}\to 2\gamma }$

ikinci dereceden Feynman diyagramı amacıyla bitişik gösterilmiştir:

In the sınır durum(altındaki; yakın zaman) burada bir elektrondur(e⁻) ve bir positron (e⁺) ve final durumu(at the üstteki;geç zaman) burada iki foton(γ)dur.

Ayrıca bakınız

• Schwinger#Schwinger ve Feynman
• Stueckelberg-Feynman yorumlamaları
• Değişmezlik Mekaniği
• Penguin diyagramı
• Yol integrali formülasyonu
• Yayıcılar
• JHepWork–Jython / Python kullanarak Feynman diyagramları çizimi için bir Java programı
• Feynman diagramlarının Listesi
• Açısal momentum diyagramları (kuantum mekaniği)

Notlar

1. "Physics and Feynman's Diagrams" by David Kaiser, American Scientist, Volume 93, p. 156
2. Feynman, Richard (1949). "The Theory of Positrons". Physical Review 76 (76): 749. Bibcode 1949PhRv...76..749F. DOI:10.1103/PhysRev.76.749. 

Kaynakça

• Gerardus 't Hooft, Martinus Veltman, Diagrammar, CERN Yellow Report 1973, online
• David Kaiser, Drawing Theories Apart: The Dispersion of Feynman Diagrams in Postwar Physics, Chicago: University of Chicago Press, 2005. ISBN 0-226-42266-6
• Martinus Veltman, Diagrammatica: The Path to Feynman Diagrams, Cambridge Lecture Notes in Physics, ISBN 0-521-45692-4 (expanded, updated version of above)
• Mark Srednicki, Quantum Field Theory, online Script (2006)

Dış kaynaklar

• AMS article: "What's New in Mathematics: Finite-dimensional Feynman Diagrams"
• WikiTeX supports editing Feynman diagrams directly in Wiki articles.
• Drawing Feynman diagrams with FeynDiagram C++ library that produces PostScript output.
• Feynman Diagram Examples using Thorsten Ohl's Feynmf LaTeX package.
• JaxoDraw A Java program for drawing Feynman diagrams.
• Bowley, Roger; Copeland, Ed (2010). "Feynman Diagrams". Sixty Symbols. Brady Haran - University of Nottingham. 8 Mayıs 2015 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20150508163457/http://sixtysymbols.com/videos/feynman.htm.