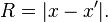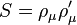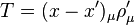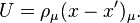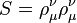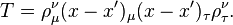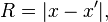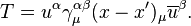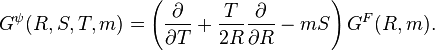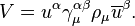Değişmezlik mekaniği

Fizikte, değişmezlik mekaniği, basitçe, Kuantum alan kuramı kurallarının sadece değişmez sayılarla yeniden yazılmasıdır.Mesela,bir parçacık kümesinin pozisyonları bir parçalı koordinat sistemi içinde sistemin çevirileri değişmezlik altında değildir. Bununla beraber, (4-boyutlu) uzunluk arasında parçacıklar sistemi çevrimler, rotasyonlar ve Lorentz dönüşümleri değişmezlik altındadır.

Bir sistemin değişmez sayıda giriş ve çıkış durumları yapımında sadece sayısal ihtiyacı olan bir olasılık genliği verir. Bir simetriye uyan sistem tarafından anlamı budur. Bundan dolayı dahil tüm miktarlar ilişki sayısıdır, değişmezlik mekaniği doğal sınır olarak görelilik kuramini alabiliyor.

Değişmez sayıda açısal momentumunun değişmezlik mekaniği kuantum çekim döngüsü ile sıkı bağlantısı vardır . Değişmezlik mekaniğinde, uzay ve zaman değişmezleri ikincil olup sadece büyük ölçekli sınırlarda yararlı kavramlar olarak görülüyor.

Feynman Kuralları

Feynman kuralları bir kuantum sisteminin değişmeyen miktarları açısından yeniden yazılabilir(kütle, yük,gibi sabitler eklenerek).Parçacığın tipi değişmez sayısına bağlıdır, skaler, vektör veya spinor. . Kurallar genellikle Feynman grafiklerinin köşelerinden Tek-yönlü formda hacimler gibi geometrik miktarları içerir

Skaler parçacıklar

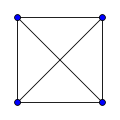
skaler parçacıklar bir sistem içinde, sadece değişmez sayıda 4-boyutlu uzunluk (ara) başlangıç noktası (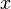$x$) ve son nokta arasi ($x'$) parçacığın yoludur. Burada bir tam grafik formun noktalari:

• 
• 
• 
• 

Değişmez sayısıdır.

$R = |x-x'|. \,$

Vektör parçacıkları

Fotonlar gibi vektör partiküllerinin olduğu bir sistem içinde,parçacık yollarının başlangıç ​​ve bitiş noktaları ve fotonların başlangıç ​​ve bitiş polarizasyon vektörleri ($\rho_\mu$) arasındaki açılar arasında 4-boyutlu mesafeleri değişmezlerdir

Burada her dört satır dört değişmezlerdir :

$R = |x-x'| \,$

$S = \rho_\mu \rho'_\mu \,$

$T = (x-x')_\mu \rho'_\mu \,$

$U = \rho_\mu (x-x')_\mu. \,$

Yang–Mills vektör parçacıkları

Yang–Mills vektör alanı ve ayrıca açı gösteriminin gauge grubu (halinde) rotasyon ilişkisi ( 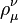$\rho^\nu_\mu$ ).

Burada her üç satır değişmezlerdir:

$R = |x-x'| \,$

$S = \rho^\nu_\mu \rho^\nu_\mu$

$T = \rho^\nu_\mu (x-x')_\mu(x-x')_\tau\rho^\nu_\tau.$

Spinor alanı

Spinor vektörler arasındaki açı ilşkisidir. Bu değişmezler:

$R = |x-x'|, \,$

$S = u^\alpha \gamma^{\alpha\beta}_5\overline{u}^\beta,$

$T = u^\alpha \gamma^{\alpha\beta}_\mu(x-x')_\mu \overline{u}^\beta.$

dir. kütlesiz skaler yayıcı'ya çok iyi bir örnek, fermiyon yayıcı'sı olarak tanımlanır.

$G^\psi (R,S,T,m)=\left( \frac \partial {\partial T}+\frac{T}{2R}\frac \partial {\partial R}-mS\right) G^F(R,m).$

Karışık sistemler

Sistemler genellikle skaler, spinor ve vektör alanlarının bir karışımından oluşur ve değişmezleri spinörleri ve vektörleri arasındaki açılara bağlıdır. Bu süreç fikirleri basitleştirmek için twistör teorisi genellikle spinörleri bir çift bir boş vektöre ayrıştırmak için bir olanak olarak kullanılır. Alternatif olarak 3 nokta değişmezleri gibi değişmeyen spinor-spinor-vektör üçgen olarak takdim edilebilir:

$V = u^\alpha \gamma^{\alpha\beta}_\mu \rho_\mu \overline{u}^\beta.$

Bu değişmezlerin bazı türlerinde, diğer değişmezlerin kombinasyonları vardır örneğin tam-grafik açı değişmezleri.. ama onlarin mesafe değişmez kombinasyonları olarak bulunabileceğine dikkat etmek gerekir. Örneğin renk dinamiğinde,4 noktalı değişmezler vardır. Yani tamamen belirtilen sistem için sistemi temsil eden tam bir grafikte üçgen ve tetrahedron her satıra atanan birkaç numara olurdu. Bir olağanüstü sorun çeşitli spin ve polarizasyon vektörleri için tüm olası değişmezlerde numaralandırma olmasıdır.

Kısıtlamalar

Tam bir grafik ile temsil edilen bir sistem birçok değişmez nicelikler içerir. Büyük grafikler için, ancak, tüm bu nicelikler bağımsız ve özel boyutlu ve ölçü kısıtlamalarını belirtmeniz gerekir. Çünkü boyutlar veya özel ölçü grubu özel sayısı seçimi hala bilinmemektedir . Bunların tam ya da yaklaşık yerinde olup olmadığını Kısıtlamalardan ve değişmezlik mekaniğinin anahtarı ve ve geleneksel alan teorisi arasındaki farktır. Çalışma bu kısıtlamaları kaldıran çekim alanının bir sonucu olup olmadığını görmek için yapılıyor. Kısıtlamalardan sadece yaklaşık olarak memnun değilseniz o zaman en iyi kullanılan özel Feynman kuralları nedeniyle meydana gelen bir sistemin genliklerinin yerel maksimum olduğu düşünülmektedir Kısıtlamalardan bir kuantum belirsizlik varsa, yani

Boyutlar

Değişmezlik mekaniği açık olarak koordinat sistemleri kullanmaz çünkü, boyut tanımı biraz farklıdır. Boyut sayısı ifadesi eşdeğer bir şekilde sistemde noktalardan yapılmış herhangi bir (D + 2)-basit hacmi sıfır olduğunu belirtmiş olarak, mesafe Öklid geometrisi olarak verilir. burada bir basit hacmi Cayley-Menger belirleyicileri tarafından verilen noktalar arasındaki değişmez mesafeleri (R) içeren bir formül ile verilmektedir.Bu belirleyici tüm basitliği ile tam olarak 0 olduğu takdirde o zaman Öklid geometrisidir.Belirleyici sadece yaklaşık olarak küçük mesafelerden sonra 0 durumunda ise uzay-zaman Öklid dışıdır.Bunun kuantum köpük ve döngüsel kuantum yerçekimi ile derin bağlantıları vardır. Minkowski uzayı için, ya da imzası ile herhangi bir alanı için (+ + + ... + -) Bu değişmezlik mekaniğinin farklı formülleri için hiç fark etmez.

Çekim

Boyutsal kısıtlamalar, kuantum belirsizliğe (denklemlerinde karşılıklı fonksiyonları ile delta fonksiyonlarının yer değiştirmesini içerir) olanak sağlayarak,öklid geometrisi artık,düz uzay-zaman ile sınırlı düz uzay-zaman sonu burada bir eğrilik olarak görülmektedir.Bu Genel Görelilik yerçekimi nedeni olarak görülebilir,burada bir eğrilik olduğu görülmektedir.Bu kapalı-kabuk fiziğine benzer şekilde kapalı-boyut fiziği olarak adlandırılır

Ölçek grubu

Boyutların sayısını ifade eden benzer şekilde, ölçü grubu boyutu ve tipi polarizasyon (veya dönüş) değişmezleri (S, T ve U) içeren bir kimlik ile verilmektedir.Bu tür foton için olduğu gibi basit bir durumda, bu Cayley-Menger'in belirleyicilerinin sadece küresel versiyonlarıdır.Ölçü grubu özel boyutlu grubu çok daha fazla nicelikler içerir çünkü ölçü grubu bir iç simetridir.Bu SU (5) veya E_6 gibi basit bir ölçü grubu U(1)xSU(2)xSU(3)(Standart Model bakınız) gibi olmayan bir basit ölçü grubuna göre daha az değişmezler içerir. Birleşik bir teori üretmek için tek bir denklem içine özel boyutlu ve ölçü kısıtlamalar birleştirerek üzerinde son çalışmaları olmuştur. Bunun tek bir karmaşık sayı (veya hypercomplex numaranın) her satırda değişmezleri birleştirerek elde edileceği düşünülmektedir.

Supersimmetri

Supersimetri modelinde,spinor değişmezler ve vektör değişmezlerinin bazıları tek bir değişmezle bir araya getirilip birleştirilir.Daha az sayıda değişmezler daha çok sayıda simetri olması bu tür dönüşümlerin fermiyonlarının ve bozonlarının arasındaki daha fazla dönüşümler olabileceği anlamına gelir.Şu anda ispatsız ama böyle olduğuna inanılmaktadır.bir sistem temsil eden tam bir grafik her satırında değişmezleri en az iki olduğunu 4-Boyutlu mesafelerde "(R)" ve başka bir parçacık 'lezzet' bir parçacık 'lezzet' dan dönmeyi "(T)" temsil eden bir açı olmaktadır. Hatta bazıları bu değişmezler uzay ve zamanın 4 boyutları olarak Evren büyüklüğü ile karşılaştırıldığında (çok az değiştirebilir olanlar olsa da, bir parçacık olabilir sadece 4 daha fazla lezzet olduğunu söyleyerek bir birleştirilebilir olduğunu ileri sürmüşlerdir tamamen). Bu tür modelleri evrenin genel bir küresel geometri olduğunu göstermektedir.Uzay-zaman ve lezzet simetrilerini karıştırma lezzet bağlı olarak her parçacık için benzersiz bir kitle olarak görünür bir parçacık ışık-konisi serbestisi ek bir derece ekler Modelin tüm karmaşıklığı değişkenlerin yüzlerce polinomları olabilir kısıtlamaları kadar bağlıdır çünkü değişmezler az sayıda olması mutlaka daha basit bir Model yapmaz. Değişmezlik mekaniğinin temel amaçlarından biri bu polinom (ları bulmak için ve karşılık gelen bu simetri grubunu bulmaktır. Birçok Bu polinom (lar) ın değişken permütasyon özel sporadik gruplarından birine karşılık geldiğine inanıyoruz. (İlginçtir, sadece büyük sporadik grubu, canavar grup Standart Modele kısıtlamalar dahil etmek kadar büyük). Diğer ana amacı hassas doğası tanımlamak ve sonsuzluklara yol açmaz her ikisi de değişmezler ile ilgili uygun Feynman kuralları bulmaktır.

M-teorisi

Değişmezlik mekaniği nokta parçacık kuramını anlamaya çalışırken doğmuş olmasına rağmen,süpersicim ve M -teorisi ile olası bağlantılarıda ortaya çıkmıştır. Argüman 4 boyutlu olması için bir kısıtlama ihtiyacı en küçük simpleks 6-tek yönlü olmasıdır. Bu zaman içinde hareket eden bir 3-simplex ( üçgen membran ) en uç noktaları olarak görülebilir . Bu fonksiyon , bir yayıcısı 6-simpleks hacminin tersi olan $1/V_6$ olacaktır. Bu 6 - simpleks hacmin 0 olduğunu ve bu nedenle 4 boyuta gömülü olduğunu,diğer bir deyişle,en yüksek olasılık olacaktır. Bu nedenle bir parçacık için boyutun kısıtlaması bir parçacığın yayıcısı ile aynı olur . Evrenin 6 simplices dışında inşa edilmiş ise O zaman boyut kısıtlama tüm simplices'lere uygulanabilir.Çalışmanın diğer alanları mesafe değişmezler sadece ayrık değerler alabilir olup olmadığını ve alanları veya hacimlerin temel değişmezleri olarak alınıp alınmadığı araştırıyor. (döngü kuantum yerçekimi nicemlenmiş alanları içerir bir çift ).

Tarihçe

Birçok kişi farkında olmadan değişmezlik mekaniği üzerinde çalışıyordu zamanını kesin olarak belirlemek zordur. Önemli kilometre taşları özel görelilik (1905),Yang-Mills ölçü değişmezleri teorisi Henri Poincaré tarafından bulunan 4 boyutlu değişmez içerir.Roger Penrose ve spin-ağlar (1960) konusunda etkiledi.Cayley-Menger ve değişmez tabanlı metrik teorisi önemli bir kilometre taşı oldu. Son zamanlarda Baratin-Freidel (2006) değişmezlik mekaniği ve döngü kuantum yerçekimi arasındaki bağlantıyı göstermiştir.

Bakınız

• Yayıcı

Dış bağlantılar

• Introduction to Invariance Mechanics
• Renormalization of Crumpled Manifolds
• Hidden Quantum Gravity in 4d Feynman Diagrams