Kuantum alan kuramı

Parçacık alan kuramı (kuantum alan teorisi), hareketli parçacık sistemlerinin kuantizasyonuyla ilgilenen parçacık mekaniğiyle benzer olarak, alanların hareketli sistemlerine parçacık mekaniğinin uygulamasıdır.

Amaç

Amacı, çok küçük ve çok yüksek enerjili parçacık sistemlerini içeren sistemlerin süreçlerini anlamaktır. Burada akla gelen ilk önemli soru genellikle şudur: Neden çok yüksek hızlı (göreli) parçacıkları, düşük hızlı (göreli olmayan) parçacıkları kuantize ettiğimiz gibi kuantize edemeyiz? Bu soru değişik bilgi seviyelerinde yanıtlanabilir. Bu yanıtlardan en temel seviyede olanı şudur: Tek bir parçacığın, "Klein-Gordon" denklemi ya da "Dirac" denklemi gibi, dalga denklemini yazmak ve bunların çözümünden eksili (negatif) enerji durumlarını ve diğer tutarsızlıkları görmektir.

Parçacık alan kuramının ilkeleri

Göreli sistemlerin göreli olmayan sistemler gibi kuantize edilememesinin yukarıda belirtilen nedeni; dikkate aldığımız sistem tek bir parçacıktan dahi oluşmuş olsa, eğer bu parçacık "göreli" hareket yapıyorsa, Einstein'in ${\displaystyle E=mc^{2}}$ denkleminin, parçacık-antiparçacık çiftlerinin yaratılmasına izin vermesinden dolayı, bu sistemi tek parçacıktan oluşmuş gibi gözönüne alamamamızdan kaynaklanır. Hatta, parçacıkların enerjilerinin toplamı kadar enerji olmasa dahi, çokparçacık durumları pek çok halde ortaya çıkar; ikinci derece "perturbasyon" kuramındaki "intermediate" durumlarda olduğu gibi. Belirsizlik ilkesinin bir diğer ifadesi olan ${\displaystyle \Delta E\Delta t\geqslant \hbar }$ eşitsizliğini dikkate alarak, bu durumların çok kısa zaman aralıklarında ortaya çıktıklarını düşünebiliriz.

Çok parçacık kuramını (parçacık alan kuramını) kullanma zorunluluğumuzun daha az belirgin bir nedeni uzayzamandaki bir noktadan bir diğer noktaya hareket yapan sistemin uyması gereken nedensellik ilkesidir.

Kaynaklar

Peskin M.E., Schröeder D.V., An Introduction to Quantum Field Theory, 1995, Addison-Wesley, s.13

Kuantum Alan Teorisi ve Tarihi

Teorik fizikte kuantum alan teorisi (QFT), yoğun madde fiziği alanında kuantum mekaniksel parçacık fiziğinde atomaltı parçacıkların modelleri ve quasi oluşturmak için teorik bir çerçevedir. Bir QFT parçacıklara, altta yatan fiziksel alanın heyecanlı durumları gibi davranır, bu yüzden bu alana quanta denir. Kuantum alan teorisinde, parçacıklar arasında kuantum mekaniksel etkileşimler karşılıklı gelen temel alanlar arasındaki etkileşim terimlerle tarif edilmektedir.

Tanım

Kuantum elektrodinamiğinin (QED) bir elektronı alan ve bir foton alanı vardır; kuantum kromodinamiklerin (QCD) kuarkın her türü için bir alanı vardır; yoğunlaştırılmış konuda, bir atom yer değişikliği alanı fonon parçacıklarına yol açmaktadır. Edward Witten, modern fiziğin "bugüne kadar"ki en zor teorisi olarak QFT yi tanımlamaktadır.

Dinamikler

Sıradan kuantum mekanik sistemlerde, her parçaçığın sonlu sayıda serbestlik decesine sahip sabit sayıda parçaçık vardır. Bunun aksine, QFT uyarılmış durumları parçacıkların herhangi bir sayısını temsil edebilir. Bu parçacık sayımı / sayı, zaman içinde değişiklikle rölativistik dinamiklerinin önemli bir özelliği olabilir, sistemlerini tanımlamak için kuantum alan teorisi özellikle yararlıdır.

Durumlar

QFT etkileşim terimleri Maxwell denklemlerindeki elektrik ve manyetik alanlar ile sarjlar arasında olanlara benzer. Ancak, Maxwell'in teorisinin klasik alanlarının aksine, QFT deki alanlar genellikle durumların kuantum super pozisyonlarında var olur ve kuantum mekaniği yasalarına tabidir.

Alanlar üzerinde sürekli miktarları olduğundan, serbestlik derecesi etkin olarak sonsuz sayıda QFT sistemlerinin sağlanması, onları parçacıkların büyük sayılarla olan durumları da bulunmaktadır. Serbestlik dereceleri sonsuz kolaylıkla hesaplanabilir miktarlar farklılaşmalara yol açabilir (örneğin, miktarlar sonsuz halde). Fiziksel olarak anlamlı sonuçlar elde etmek için, bu QFT parametrelerinin yeniden normalizasyonu veya QCD olarak uzay zamanı ayrıklaştırma gibi teknikler, genellikle bu tür sonsuzlukların önlemek için kullanılır.

Alanlar ve Radyasyon

Yerçekimi alanı ve elektromanyetik alan doğada sonsuz bir yelpazesi olan iki temel alanlardır ve onların "parçacık benzeri" uyarımları gizleyen klasik düşük enerjili sınırı vardır. Albert Einstein 1905 yılında, elektromanyetik alana "parçacık benzeri" ve momentumlarının ve enerjilerin ayrık değişimleri, karakteristik "alan quanta" ya atfetti. Orijinal olarak, onun başlıca motivasyonu radyasyonun termodinamiğini açıklamak oldu. Fotoelektrik etki ve Compton fotonun varlığını düşündürmektedir. Kuvvetle saçılma olsa da, dönüşümlü emisyon sadece nicemleme ile açıklanabilir; radyasyonun kuantum doğası daha kesin kanıtlar, antibunching etkisi gibi, modern kuantum optik içine alınır.

Teoriler

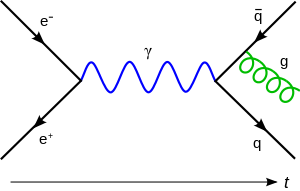
Kalan temel kuvvet, yerçekimi açısından şu anda tam kuantum teorisi şu anda yoktur. Önerilen teorilerin çoğu yerçekimi açıklamak içindir, bir QFT yerçekimi kuvvetine aracılık eden bir çekimsel parçacığın varlığına inanmaktayız. Muhtemelen, yerçekimi alanının henüz bilinmeyen doğru kuantum alan teorisi düşük enerjili limiti Einstein'ın görelilik genel teorisi gibi davranacaktır. Temel kuvvetlerin kendisi kuantum alan teorisi gibi süper sicim teorisi gibi daha temel bir teori düşük enerjili etkin alan teorisi sınırı olduğu için ileri sürülmüştür. Standart parçacık fiziğindeki çoğu teoriler, QED, QCD ve Standart Modeli gibi göreli kuantum alan teorileri olarak formüle edilir. QED, elektromanyetik alanın kuantum alan teorisi açıklamaya yaklaşık sanal elektron-pozitron çiftleri nedeniyle gerekli Maxwell denklemleri küçük doğrusal olmayan düzeltmeler, düşük enerjili limiti elektrodinamik Maxwell'in teorisini yeniden üretir. Kuantum alan teorisi için pertürbatif yaklaşımda, tam saha etkileşim terimleri dahil parçacıkların sayısında tedirgemeli genişleme olarak yaklaştırılır. Genişlemenin her döneminde parçacıklar arasındaki kuvvetler, diğer parçacıklar ile aracılık edilen şekilde düşünülebilir. QED, iki elektron arasında elektromanyetik kuvvet fotonların değişiminden kaynaklanır. Benzer bir şekilde, ara vektör bozonlar az bir kuvvete aracılık ve gluonlar QCD güçlü kuvvete aracılık eder. Bir kuvvet aracı parçacık kavramı pertürbasyon teorisinden gelir ve bağlı durumlar gibi QFT, pertürbatif olmayan yaklaşımlar bağlamında anlam ifade etmemektedir.

Tarihçe

Buluşlar

Alanın erken gelişimi Dirac, Fock, Pauli, Heisenberg ve Bogolyubov’u kapsadı. Gelişmenin bu aşaması 1950'lerde kuantum elektrodinamik teorisi yapımı ile sonuçlandı.

Gauge Teorisi

Gauge teorisi, parçacık fiziğinin standart modelinde somutlaşan güçlerin birleşmesine nicelik ve formüle oldu. Bu çaba Yang ve Mills’in çalışmaları ile 1950'lerde başladı, 1960'lar boyunca Martinus Veltman ile devam etti, 1970'lerde Gerard 't Hooft, Frank Wilczek, David Gross ve David Politzer çalışmalarıyla tamamlandı.

Büyük Sentez

Yoğun madde fiziği faz geçişleri anlayışında paralel gelişmeler yeniden normalizasyon grubunda çalışmaya yol açtı. Bu da kuantum alan teorisi ile partikül ve yoğun madde fiziği teorilerinde birleşik teorik fizik, büyük sentezine yol açtı. 1975 yılında Kenneth G. Wilson tarafından kuantum alan teorisinda yeni ufuklar açan formüle edilen durum, 1970'lerde Michael Fisher ve Leo Kadanoff'un çalışmalarını içeriyordu. İlkeler

Klasik ve Kuantum Alanlar

Bir klasik alan, uzay ve zamanın bazı bölgeleri üzerinde tanımlı bir fonksiyondur. Klasik alanlar tarafından açıklanan iki fiziksel olay Newton yerçekimi alanı g (x, t) ve elektrik ve manyetik alanlar E (x, t) ve B (x, t) tarafından açıklanan klasik elektromanyetizmadır. Bu tür alanlar prensipte uzayda her noktada farklı değerler alabilir çünkü onların özgürlüğünün sonsuz derecede olduğu söylenir. Klasik alan teorisi, bu tür fiziksel fenomenlerin kuantum-mekanik yönlerini dikkate almaz. Örneğin, bu elektromanyetizmanın bazı yönleri ayrı parçacıklar-fotonlardan ayrı olarak sürekli alanları içeren kuantum mekaniği olarak bilinmektedir. Kuantum alan teorisi klasik alanda, uzay ve zaman içinde tanımlanmış bir fonksiyonu, aynı zamanda kuantum mekaniğinin gözlemlerini barındırmaktadır. Bu kuantum alandır. Bu kuantum mekaniği alan teorisinin aksine bir yapıya sahip olduğundan, böyle bir kuantum alanını yazmak açık değildir. En genel formülasyon da kuantum mekaniği, gözlenebilir ve fiziksel gözlemlenebilir miktarları ve durum uzay çalışma kapsamında sistemin olası durumlarını temsil ettiği soyut durum uzayında (Hilbert uzayı), üzerinde soyut operatörler (gözlenebilirlerin) olduğu bir teoridir. Örneğin, tek bir kuantum mekanik parçacığın hareketi ile ilişkili temel gözlenebilirlerinin konum ve momentum operatörleri \ şapka {x} ve \ şapka {s} bulunmaktadır. Alan teorisinin, aksine, saha indeksi operatörden ayrı bir yol olarak x davranır. Kuantum alanını geliştirmenin iki ortak yolu vardır; Yol integrali formalizmi ve kanonik kuantizasyon. Bunlar bu makalede sürdürülmektedir.

İlişkili Olaylar

Makalenin önceki bölümünde, kuantum alan teorileri en genel özellikleri ile açıkladık. Teorik fizikte çeşitli alanlarda çalışılan kuantum alan teorilerinde bazıları, renormalizability, gösterge simetri ve süpersimetri gibi ek özel fikirler içerir. Bunlar aşağıdaki bölümlerde açıklanmaktadır

Renormalizasyon

Erken kuantum alan teorisi tarihinin, bulunmuştur ki elektromanyetik alanın varlığı böyle bir elektronun enerjisinde tedirgeme kayması gibi görünüşte hesaplamalar olduğu, sonsuz sonuçlar verdiği görülmüştür. Enerji geçiş için pertürbasyon teorisinin nedeni, diğer tüm enerji seviyeleri üzerinde bir miktar içerdiğini ve her bir farklı seride sonuçlanan sonlu bir katkı vermek, kısa mesafelerde ise birçok seviyeleri vardır. Bu sorunların çoğu 19. yüzyılda tanımlanan ancak faili meçhul edilen klasik elektrodinamik arızalarla ilgili ve onların temelde bir elektronun sözde "içsel" özelliklerinin çoğunu elektromanyetik alana bağlı gerçeğinden kaynaklanıyor olmasıdır. Tek bir elektron-kendinin taşıdığı enerji, sadece çıplak bir değer değil, aynı zamanda onun elektromanyetik alanı, fotonların bulut içerdiği enerji içerir. Küresel kaynağının alandaki enerjide, hem klasik ve hem kuantum mekaniğinin ayrıldığı, ancak Furry nin yardımıyla Weisskopf tarafından keşfedilen, kuantum mekaniğinde ayrışmanın çok hafif olduğunu ve sadece kürenin yarıçapının logaritma olarak gitmesidir. Problemin çözümü, Stueckelberg tarafından önerildiği, Bethe tarafından, önemli deneyden sonra Lamb tarafından, tek döngü uygulauan Schwinger tarafından, yakınsama ile Feynman ve Dyson tarafından, sistematik izole savaş sonrası Japonya'da Tomonaga tarafından çalışmalarıdaı tüm döngüler uzatıldı, özellikle elektronun kütlesi ve şarj: fotonların ve elektronların etkileşimleri tüm sonsuzluklar için gözlenen değerler ile bunları değiştirerek denklemlerde miktarların sonlu sayıda yeniden tanımlanması ve izole edilebilir olduğunu kabule renormalizasyon denir. Renormalizasyon tekniği, problemin son derece kısa mesafelerde hatalı olduğunu, esasen tamamen matematiksel olduğunu kabul eder. Bir süreklilik içinde bir teori tanımlamak, quanta nın bazı son derece yüksek değerin üstünde enerjilere sahip olamayacağını varsayarak, alanlarda bir kesme yerleştirmek için önemlidir. Bu çok kısa dalga boyları bir kafes olduğu gibi, mevcut olmayan bir yapı ile sürekli boşluğu değiştirme etkisine sahiptir. Kafesler dönme simetrisini kırmak ve Feynman, Pauli Villars'daki tarafından yapılan önemli katkılarından biri, ve t Hooft ve Veltman 'tarafından modernize edilen, pertürbasyon teorisi için bir simetri koruyucu kesme dir. (bu işleme regularization denir). Titiz ya da sayısal iş için insanlar genellikle gerçek bir kafes kullanır, böylece bilinen simetrik kesme, pertürbasyon teorisinin dışında bulunmaktadır. Bir kafes üzerinde, ancak aralığa bağlı olarak her miktar sonludur. Sıfır aralık limitini çekerken, gözlenen elektron kütlesi gibi fiziksel gözlemlenebilir miktarların teorisini tanımlayan Lagrangian sabitleri aralığa bağlıdır anlamına gelir. Umarım, sabitlere kafes aralığı ile farklılık izin vererek, uzun mesafelerde tüm sonuçlar bir süreklilik sınırını tanımlayan, kafes için duyarsız hale gelir. Renormalizasyon işlemi sadece renormalize kuantum alan teorisi denilen kuantum alan teorileri belli bir sınıf için çalışmaktadır. Lagrangian sabitler, sadece çok kısa aralıklar için kafes aralık logaritma olarak sapmak bir teori tedirgemeyle renormalize olduğudur. Süreklilik sınırı sonra iyice pertürbasyon teorisi ile tanımlanır ve tamamen iyi olmayan tedirgemeyle tanımlı olmasa bile, sorunlar sadece zayıf bağlantı elemanları için ters bağlantı katlanarak küçük mesafe ölçeklerinde yer almaktadır. Parçacık fiziğinin Standart Modeli tedirgemeli renormalize ve böylece bileşen teorileri (kuantum elektrodinamik / elektrozayıf teori ve kuantum kromodinamikleri) vardır. Asimptotik serbest SU (2) ve SU (3) zayıf hiper şarj ve güçlü renk etkileşimleri nonperturbatively iyi tanımlanmış ise üç bileşenden, kuantum elektrodinamiğin, bir süreklilik sınırı yok olduğuna inanılmaktadır. Renormalizasyon grubu, renormalize teorilerinin herhangi bir yüksek enerjili teorisi için uzun mesafe düşük enerjili etkin alan teorisi olarak açıklamaktadır. Bu nedenle, renormalize teorileri yatan yüksek enerjili kısa mesafe olayların kesin doğasına duyarsızdır. Bu fizikçilerin yüksek enerji fenomeni ayrıntılarını bilmeden, düşük enerji teorileri formüle etmelerini sağlar. Standart model gibi bir renormalize teori çalışması bulunursa, bu kez daha yüksek enerji süreçlerine çok az ipucu vermektedir. Aksi takdirde yasak olayları izin verdiğinizde, ya da birleştirme sabitleri arasındaki niceliksel ilişkiler varsa yüksek enerji süreçleri standart modelinde görülebilir tek yoldur.

Haag Teoremi

Bir matematiksel perspektiften bakıldığında, Lorentz-kovaryant kuantum alan teorisinde hiçbir etkileşim mevcut değildir.

Bu QFT içinde Feynman diyagramlarının pertürbatif yaklaşımı kesinlikle deney tarafından onaylanmış çok hassas tahminler üretmesine rağmen, haklı olmadığı anlamına gelir. Buna Haag teoremi denir, ama parçacık fizikçileri QFT güvenerek büyük ölçüde onu silkmektedirler.

Gauge Özgürlüğü

Gauge teorisi yerel parametre ile bir simetri teorisidir. Örneğin, her kuantum teorisinin dalga fonksiyonunun global fazı fiziksel bir şey temsil etmez. Sonuç olarak, teori fazlarının bir küresel değişimi (her yerde, her dalga fonksiyonlarının fazına sürekli ekleme) altında değişmez olduğudur; bu küresel simetri olduğunu belirtir. Kuantum elektrodinamik, aynı zamanda faz yerel değişikliği altında değişmez - shift uzay-zamanda her noktada farklı olabilir ki bütün dalga fonksiyonlarının fazı kayabilir. Bu yerel bir simetri olduğudur. Ancak, varlığını iyi tanımlanmış bir türev operatörü için sırayla, bir de türevi etkilemeyecek değişkenlerin yerel değişimi (bizim örneğimizde faz) için sırayla dönüştüren yeni bir alan, gösterge alanını tanıtmak gerekir. Kuantum elektrodinamikte bu gösterge alanı elektromanyetik alandır. Değişkenlerin yerel göstergesine değişim göstergesi dönüşümü denir. Bu Noether teoremi ile her tür simetri için bir birleşik muhafaza akımı var olduğunu belirtmiştir. Küresel faz değişiklikleri altında dalga fonksiyonunun yukarıda belirtilen simetri elektrik yükünün korunumu ima eder. Kuantum alan teorisinde alanların eksitasyonları parçacıkları temsil etmektedir. Gösterge alanının uyarımları ile ilişkili parçacık kuantum elektrodinamik durumunda foton olan gösterge bozonu vardır.