Ayar kuramı
| Parçacık fiziğinin standart modeli |
|---|
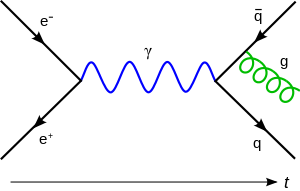
{{{altyazu}}} |
|
Bileşenleri
|
|
Sınırları
|
Ayar kuramı (İngilizce: Gauge theory) , kuramsal fizikte temel etileşmeleri açıklar. Türkçede bazen yerelleştirilmiş bakışım kuramı olarak da geçer.
Fizikte, bir Yerelleştirilmiş Bakışım Kuramı (Gauge Teorisi) Lagrange yerel dönüşümlerin sürekli gruplar altında değişmez değerlerin olduğu alan teorisinin bir türüdür.
Terim olarak yerelleştirilmiş bakışım Lagrangian içindeki gereksiz serbestlik derecelerine işaret eder. Ayar dönüşümleri denilen olası göstergeleri arasındaki dönüşümler, bir Lie grubu-sevk simetri grubu ya da teorinin gösterge grubu olarak oluşturur. Grup jeneratörlerin Lie cebiri herhangi Lie grubu ile ilişkilendirilmiştir. Her grup jeneratör için mutlaka bir karşılık gelen alan (genellikle bir vektör alanı) gauge alanı denilen alan ortaya çıkar. Gauge alanları yerel grup dönüşümleri altında değişmezliği (denilen gauge değişmezliği) sağlamak için Lagrange dahildir. Böyle bir teori nicemlenmis olduğunda, Gauge alanlarının kuantumuna Gauge bozonları denir. Simetri grubu değişmeli değil ise ise, normal olan örnek Yang-Mills teorisidir.
Fizikteki birçok güçlü teoriler Lagrangeler altında sabit simetrik dönüşüm grupları tarafından açıklanmıştır. Onlar aynı fiziksel süreçler ortaya çıktığı zaman uzayın her noktasında yapılan bir dönüşüm altında değişmezdir, onların küresel bir simetriye sahip olduğu söylenir. Gauge teorilerinin temel taşı olan yerel simetri daha sıkı bir engeldir. Aslında, küresel simetri uzayda sabitlenmiş olan yerel simetrinin grup parametlereleridir.
Guage teorileri temel parçacıkların dinamiklerini açıklayan başarılı alan teorileri kadar önemlidir. Kuantum elektrodinamiği gauge teorisinin simetrik grubu U(1) ile değişmelidir. Kuantum elektrodinamiği bir tane gauge alanına sahiptir. Standart Modelin toplamda oniki tane gauge bozonu vardır. Bunlar foton, üç tane zayıf bozon ve 8 tane gluondur. U (1) SU × simetri grubu ile değişmeli olmayan gauge teorisi (2) × SU (3) ve oniki bozonlarının toplam vardır: fotonun, üç zayıf bozonları ve sekiz gluonların.
Gauge teorileri genel görelilik teorisi içindeki yerçekimini açıklamada önemlidir. Onun vaka göstergesi alan bir tensör, Lanczos tensör olduğunu biraz benzersizdir. Gauge çekim teorisi ile başlayan kuantum yerçekimi teorisi, aynı zamanda kütleçekimi olarak bilinen bir ölçü bozonunun varlığına inanmaktayız. Gauge simetrilerinin koordinat sistemi uzay keyfi diffeomorphisms altında serbestçe seçilebilir olduğu genel genel görelilik kovaryans ilkesi analogları olarak görülebilir. Hem gauge değişmezliği ve Diffeomorfizm değişmezliği sisteminin açıklamasında bir fazlalık göstermektedir. Bir alternatif kütleçekimi teorisi olarak gauge kütleçekim teorisi yeni gauge alanları ile gerçek bir gauge ilkesinin genel kovaryans ilkesini değiştirir.
Tarihsel olarak, bu fikirler ilk klasik elektromanyetizma bağlamında ve daha sonra genel görelilik ile belirtilmiştir. Ancak, gauge simetrilerinin modern fizikteki önemi elektron göreli kuantum mekaniğiyle ilk olarak ortaya çıktı. Bugün, Gauge teorileri yoğun madde fiziğinde, nükleer ve yüksek enerji fiziğinde ve diğer alt başlıklar arasında yararlıdır.
Geçmişi
Bir gauge simetriye sahip ilk alan teorisi, 1864-65 yılında, Maxwell'in formülasyonu olan elektrodinamiktir. ( "Elektromanyetik Alan Bir Dinamik Teorisi"). Bu simetrinin önemi erken formülasyonlarda fark edilememiştir. Benzer şekilde farkedilemeyen, Hilbert'ın Einstein'ın alan denklemlerinden türettiiği genel koordinat dönüşümü altında eylem değişmezliğini varsaymıştı. Daha sonra Hermann Weyl, genel görelilik ve elektromanyetizma birleştirmek amacıyla, ayar (ya da "Gauge") değişikliği altında genel görelilikte yerel simetri olabileceğini tahmin etti. Kuantum mekaniğinin gelişiminden sonra Weyl, Vladimir Fock ve Fritz london karmaşık bir miktar ayar katsayısını değiştirerek gague değiştirilmiş oldu ve U (1) gauge simetrisi olan faz değişikliği içine ölçekli dönüşüme döndü. Bu olay yüklü kuantum mekaniksel parçacığın dalga fonksiyonu üzerinde elektromanyetik alan etkisi olarak açıklandı. Bu 1940'larda Pauli tarafından yaygınlaştırılan ilk tanınmış ayar teorisi, oldu.[1]
1954 yılında, temel parçacık fiziğinde büyük bir karışıklığı bazı çözmek için çalışırken, Chen Ning Yang ve Robert Mills birlikte atom çekirdeklerindeki nükleonları tutan güçlü etkileşimi anlamak için model olarak değişmeyen gauge teorileri tanıtıldı. (Ronald Shaw, Abdus Salam altında çalışan, bağımsız doktora tezi aynı kavramını tanıttı.) Elektromanyetizma göstergesi değişmezliği yaygınlaştırılması, onlar (non-değişmeli) SU (2) simetri grubunun eylem dayalı bir teori inşa etmek için proton ve nötronların isospin duble üzerinde çalıştı. Bu, kuantum elektrodinamik spinör alanları U (1) grubunun hareketine benzerdir. Parçacık fiziğindeki odak kuantize gauge teorilerini kullanarak oldu.
Bu fikir daha sonra kuantum alan teorisinin zayıf kuvvet uygulaması ve elektrozayıf teoride elektromanyetizma ile birleşmesine vesile oldu. Değişmez gauge teorileri asimptotik özgürlük olarak adlandırılan bir özellik ile yeniden fark edildiğinde gauge teorileri daha da çekici hale geldi. Asimptotik serbestlik güçlü etkileşimlerin önemli bir özelliği olduğuna inanılıyordu. Bu güçkü kuvvetler için gauge teorisini aramaya taşvik etti. Şimdi kuantum renk teorisi olarak bilinen bu teori, kuarkların renk üçlüsü SU (3) grubunun eylemi ile birlikte bir gauge teorisidir. Standart Model, gauge teorisi dilinde elektromanyetizma, zayıf etkileşimler ve güçlü etkileşimlerin açıklamasını birleştirir.
1970'li yıllarda, Sir Michael Atiyah klasik Yang-Mills matematiksel denklemlerinin çözümlerinin çalışsmasına başladı. 1983 yılında, Atiyah'ın öğrencisi Simon Donaldson pürüzsüz 4-manifoldları türevlenebilir sınıflandırma ile homeomorfizma kadar onların sınıflandırmadan çok farklı olduğunu göstermek için bütün çalışmasını bunun üzerine inşa etti. Michael Freedman Öklid 4-boyutlu uzayda üzerinde egzotik R4 Stürevlenebilir yapılarını sergilemek için Donaldson çalışmalarını kullandı. Bu temel fizik başarılarından bağımsız, kendi iyiliği için gauge teorisi giderek artan ilgiye yol açtı. 1994 yılında, Edward Witten ve Nathan Seiberg bazı topolojik değişmezler (Seiberg-Witten değişmezler) hesaplanmasını etkin Süpersimetri dayalı gauge teorisinin tekniklerini icat etti. Gauge teorisinden matematiğe olan bu katkılar bu alanda yenilenmiş bir ilgiye yol açmıştır.
Fizikteki gauge teorilerinin önemi elektromanyetizmanın kuantum alan teorisi açıklamak için birleşik bir çerçeve, zayıf kuvvet ve güçlü kuvvet sağlayan matematiksel biçimcilik gibi muazzam başarılara örnek olmuştur. Standart Model olarak bilinen bu teori, doğanın dört temel kuvvetten üçüne ilişkin deneysel tahminleri açıklar. Sicim teorisi gibi modern teorilerin, yanı sıra genel görelilik, teorilerinin içinde bir şekilde gauge teorileri vardır.[2]
Tanımı
Global ve Lokal Simetriler
Global Simetri
Fizikte, herhangi bir fiziksel durum için matematiksel açıklama, genellikle fazla serbestlik dereceleri ihtiva eder; aynı fiziksel durum ise, aynı zamanda birçok eşdeğer matematiksel yapılandırmalar için tarif edilir. Bu dönüşümler teorinin "simetrileri" bir grubu olduğu, ve fiziksel durumu bağımsız bir matematik yapılandırmaya ancak bu simetri grubu ile birbirine bağlı sınıflardaki konfigürasyonlarda karşılık gelir.
Bu fikir tüm fiziksel sistemi kapsar hiçbir tercih "eylemsizlik" koordinat sistemi vardır bir durumda çok daha soyut "koordinatların değişiklikler" benzer yerel yanı sıra küresel simetri içerecek şekilde genel olabilir. Bir gauge teorisi modelin simetrileri ile birlikte tutarlı fiziksel tahminler yapmak için gerekli teknikler sete sahip bir matematiksel modeldir.
Global Simetriye Örnek
Matematiksel konfigürasyonda meydana gelen miktarı sadece bir sayı değil de bir hız ya da bir dönme ekseni, bir vektör veya bir matris halinde düzenlenmiş sayıları da koordinat transformasyonu ile değiştirilebilir olarak geometrik öneme sahip olduğunu temsili olarak görmek gerekir.
Lokal Simetri
Lokal Simetriyi tanımlamak için lif demetlerinin kullanılması
Gauge teorilerinin çoğunda, uzay ve zamanda bireysel bir noktada soyut ölçü bazında olası dönüşümlerin kümesi sonlu boyutlu Lie grubudur. En basit şekliyle böyle bir grup karmaşık sayılar kullanımı yoluyla kuantum elektrodinamik (QED) modern formülasyonu görünen U (1) 'dir. Kuantum elektrodinamik genellikle ilk ve en basit fiziksel ölçü teorisi olarak kabul edilir. Belirli bir gauge teorisinin tüm yapılandırma için mümkün gauge dönüşümlerinin kümesi de bir grup oluşturmaktadır. Bu grupta gauge grubunun teorisini oluşturmaktadır. Gauge grubunun bir elemanı (sonlu boyutlu) Lie grubu, örneğin her noktada fonksiyonun değerini ve türevlerinin göstergesi dönüşüm eylem üzerinde temsil ettiği için uzay-zamanın noktalarından bir düzgün değişen fonksiyonu tarafından değiştirilebilen bu nokta üzerindedir.
Uzay ve zaman içinde her noktada sabit bir parametre ile bir gauge dönüşümü geometrik koordinat sisteminindeki katı bir rotasyona benzerdir. Bu gauge temsilinin küresel simetrisini temsil eder. Sert bir dönüş durumunda olduğu gibi, bu gauge dönüşümü gerçekten yerel miktarı temsili ile aynı şekilde gauge bağımlı miktarının bir yol boyunca değişiklik oranını temsil eden ifadeleri etkiler. olan parametre sabit fonksiyon yerel simetri olarak adlandırılır olmayan bir göstergesi dönüşümü; Bir türev içeren ifadeler üzerindeki etkisi yok ifadelerden o niteliksel olarak farklı olduğunu. (Bu Coriolis etkisi üretebilir referans çerçevesi olmayan bir atalet değişimine benzer.)
Gauge Alanları
Gauge alanı matematiksel yapılandırmayı açıklamak için önemli bir parça haline gelir. Gauge alan bir gauge dönüşümü ile yok edilebilecek bir yapılandırma (matematiksel dili, kendi eğriliği olarak) kendi alan şiddeti her yerde sıfır özelliğine sahip; Gauge teorisi bu yapılandırmalar ile sınırlı değildir. Başka bir deyişle, bir gauge teorisinin ayırt edici özelliği gauge alanı sadece koordinat sisteminin kötü bir seçimi ile telafi olmamasıdır. Başka bir deyişle genellkile gauge alanını yok eden hiçbir gauge dönüşüm yoktur.
Bir gauge teorisinin dinamiklerini analiz ederken, gauge alanı dinamik bir değişken gibi davramalıdır. Ek olarak diğer nesneler ile etkileşimi yüzünden gauge alanı tipik olarak "kendi kendine enerji" terimi şeklinde enerjiye katkıda bulunur. Gauge teorisi için denklemleri elde etmek için
- gauge alanı olmadan naif başlangıç
- (Genel olarak, bir dönme açısı için soyut eşdeğeri) sürekli bir parametre ile karekterize edilebilir teorinin kişilerce genel simetri listesi;
- bir yerden başka bir yere değişen izin verlien simetri parametresinden kaynaklanan düzeltme terimlerini hesaplamak;
- Bir veya daha fazla ölçü alanlarına kavramaları olarak bu düzeltme terimleri yeniden yorumlanmasına ve bu alanları uygun öz-enerji terimleri ve dinamik davranışı vererek.
Bu bir anlamda gauge teorisinin global simetriden lokal simetriye uzanıştır. Ayrıca bu oldukça yakın bir şekilde gauge kütle çekimi teorisinin bilenen adıyla genel görelilik teorisinin tarihsel gelişimini andırıyor.
Fiziksel Deneyler
Gauge teorilerinin esas fiziksel deneylerin sonuçlarını modellemek için
- evreni sınırlayan olası yapılandırmaları deneyi kurmak için bilgilerle uyumlu olanlar
- deneyi ölçmek için olası sonuçların olasılık dağılımı hesaplama
bu ikisi kullanılır.
Özel bir referans olmadan genellikle deneyin kurulum bilgileri ve olası ölçüm sonuçları matematiksel açıklamalarla anlatılamaz buna gauge seçimide dahildir. Gauge teorisinin hesaplamalarında anormalliklerin sık görülen kaynağı hor kullanılan sınır durumlardaki gauge bağımlılığıdır.
Süreklilik teorileri
(Süreklilik elektrodinamik ve genel görelilik) Yukarıda belirtilen iki gauge teorileri süreklilik alan teorileri örnekleridir. Süreklilik teorisindeki hesaplama tekniklerini dolaylı olarak varsayarız:
- gauge tamamen sabit seçenek sunulur, tek bir yapılandırma sınır koşulları prensipte tamamen tarif edilebilir
- tamamen sabit gauge ve sınır koşulları komple bir set verilen en az eylem ilkesi, bu sınırları ile tutarlı eşsiz bir matematiksel bir yapılandırma (ve dolayısıyla eşsiz bir fiziksel durum) belirler;
- muhtemel ölçüm sonuçları olasılığı ile belirlenebilir:
- kurulum bilgileri ile tutarlı sınır koşulları tarafından belirlenmektedir tüm fiziksel durumlar üzerinde bir olasılık dağılımı kurulması,
- Her olası fiziksel durum için ölçüm sonuçlarının bir olasılık dağılımı kurulması,
- Bu iki olasılık dağılımlarını toplamının olası bir ölçüm dağıtım kurulum bilgileri ile tutarlı sonuçlarını almak için;
- Gauge sabitlemek hesaplamalarda anormalik göstermez.
Bu varsayımlar, enerji ölçekleri ve deneysel koşullar için geniş bir yelpazede geçerlidir. Bu teoriler ışığında, günümüzde karşılaşılan ışıktan ısı ve elektrik düşüşlerinden ve yükselmelerinden gelen bütün fenomenleri doğru tahmin etmede kullanılır. Bu tahminler sadece çok küçük ve çok büyük ölçeklerde doğru değildir.
Kuantum Alan Teorileri
Bu klasik süreklilik alan teorileri dışında, en yaygın olarak bilinen gauge teorileri, kuantum elektrodinamik ve temel parçacık fiziğinin Standart Modeli dahil kuantum alan teorisi vardır. En az eylem ilkesine göre "izin verilen" fiziksel durumları niteleyen bir gauge-kovaryantı eylem ayrılmaz. Ancak, gauge dönüşümleri tarafından aşırı derecelerde sebest davranışlarından dolayı süreç (continuum) ve kuantum teorileri büyük farklılıklar göstermektedir. Süreç (continuum) teorileri ve basit kuantum alan teorilerinin çoğu matematiksel düzenlemelerin yörüngelerini düşürmeden gauge reçetesini kullanırlar.
Daha sofistike olan kuantum alan teorileri özellikle değişme olmayan gauge gruplarını içerenler başta olmak üzere gauge simetrisine karışıklık teorisi teknikleriyle yok ederler ve ve karşı terimler BRST nicelemesinde bilindiği gibi birbirlerini anormal bir şekilde iptal etmek için motive ederler. Bu endişeler bir anlamda son derece teknik olmakla birlikte, aynı zamanda yakından ölçümü, fiziksel bir durum bilgisine sınırları ve eksik belirtilen deneysel koşullar nedeniyle tam olarak anlaşılmamıştır. Matematiksel teknikler işlenebilir gauge teorilerini uygulamak için birçok alanda geliştirildi. Bunlara örnek düşük boyutlu topoloji katı hal fiziği ve kristalografisi verilebilir.
Klasik Gauge Teorisi
Klasik Elektromanyetizma
Tarihsel oalrak, Gauge simetrisinin ilk örneğinin keşfi klasik elektromanyetizmadır. Elektrostatikte, elektrik alan E ya da onun karşılığı elektrik potensiyel V . bu hariç, elektrik alan ya da elektrik potensiyelden birnin bilinmesi muhtemelen diğerinin bulunmasını sağlar. elektrik alan uzayda bir noktadan diğerine potansiyel değişimlerle ilgilidir. Vektör hesabı açısından, elektrik alan potensiyelin negatif değişim derecesine eşittir.. Elektrostatikten elektromanyetizmaya genellersek, elimizde ikinci bir vektor potensiyeli A ile
Genel Gauge dönüşümü sadece değildir.
Burada f zamana ve pozisyona dayalı herhangi bir fonksiyondur. Gauge dönüşümleri altında alanlar aynı kalır ve sonuç olarak Maxwell denklemleri hala geçerlidir. Buda Maxvell denklemlerinin gauge simetrisine sahip olduğunu söyler.
Skaler Gauge Teorisin Örneği
Aşağıdaki formüllerle sezgisel küresel simetri özelliklerinden başlayarak "motive" nasıl yerel gauge değişmezliği gösterir ve başlangıçta olmayan etkileşim alanları arasındaki etkileşime nasıl yol açar. Aşağıdaki formüllerle örneklendirilmiştir.
n burada etkileşime girmeyen gerçek skaler alanlar, m burada kütleye eşittir. Sistem burada hareket halindedir. ve toplam hareket halindeki skaler alanlar
Lagrange(yoğunluğu) küçük sıkı bir şekilde yazılabilir.

Alanların vektörünün gösterimiyle
4 boyutun her birinde Terim olan Einstein simgesi kısmi türevidir. Dönüşümün altındaki değişmeyen Lagrange şimdi daha şeffaf oldu.
G n-by-n ortogonal gruba ait olan sabit matrisdir. türevi benzer biçimde ve her iki nicelikte nokta çarpımının içindeki Lagrange belirdiği için Lagrange'nin korunuduğu görünür.
Bu bu özel Lagrangian küresel simetri karakterize ve simetri grup genellikle ölçü grubu denir; Matematiksel terim özellikle G-yapıların teorik olarak yapı grubudur. Bu arada, Noether teoremi dönüşümleri bu grup altında değişmezlik akımların korunmasına yol açtığını ima edilir.
Burada Ta matrisleri SO(n) gruplarının jeneratörleridir. Her jeneratör için korunmuş bir akım vardır.
Şimdi Lagrangian lokal değişmeyen O(n) sahip olmalıdır. G matrisleri x kordinatında uzayzaman fonksiyonun olmasına izin vermelidir.
Bu durumda G=G(x) iken G matrisi geçemez.
Bu sorunu çözmek için yeni bir türev alırız.
Bu yeni türev eşdeğişken gauge türevi olarak adlandırılır ve bu forma sahiptir.
Burada g eşleşen sabit olarak adlandırılır ve etkileşimin gücünü tanımlamada önemlidir. Basit birkaç hesaplamadan sonra Gauge Alanı A(x) aşağıdaki gibi dönüşmek zorundadır.
Gauge alanı Lie cebirinin bir elementidir. Sonuç olarak aşağıdaki gibi genişletilebilir.
Son olarak şimdi elimizde lokal Gauge değişmeyen bir Lagrangian' ımız var.
Bu Lagrange ve özgün küresel gauge değişmeyen Lagrangian arasındaki fark Lagrange Etileşimi olduğu görülür.
Bu terim sadece yerel gauge değişmezliği için talebin bir sonucu olarak n skaler alanlar arasındaki etkileşimleri tanıtır. Bununla birlikte, bu etkileşimin fiziksel olup tamamen rastgele hale getirmek için, arabulucu A (X) uzayda yayılması gerekir. Bununla başa çıkmak için bir sonraki aşama teriminin Lagrangiana eklenmesidir. Elde edilen klasik alan teorisi kuantize sürümünde, kuantum gauge alanı A (x) gauge bozonları denir. Kuantum alan teorisinde Lagrangian etkileşiminin yorumlanması skaler bozonların değişen gauge bozonlarıyla etkileşimidir.
Gauge alanı için Yang-Mills Lagrangesi
Bir önceki bölümde geliştirilen bir klasik gauge teorisinin çizilen o resmi nerdeyse bitmek üzere. Uzayzamanda ki gauge alan A(x) değerinin bulunması için sadece eşdeğişken türvelerin (D) tanımlanması kaldı. Bu alanın manuel değerlerini belirlemek yerine, bu bize alan denklemlerinin çözümünü verilebilir. Dahası bu alan denkleme Lagrange yanı sıra yerel gauge değişmez olduğunu gerektiren, gauge alanı için Lagrangian olası bir formu (geleneksel) şeklinde yazılır
ile
ve İzler vektör uzay alanları üzerinden atılıyor. Buna Yang-mills hareketi denir. Diğer gauge değişmez haretleri hala mevcuttur. Örneğin doğrusal olmayan elektrodinamik, Born-Infeld hareketi Chern-Simons model gibi.[3]
Gauge teorisi için tamamlanmış Lagrangian aşağıdaki gibidir.
Elektrodinamiğe Örnek
Daha önceki bölümlerde geliştirilen biçimcilik basit bir uygulama olarak, sadece elektron alanı ile, elektrodinamik davayı düşünün. Bare-bones hareketi elektirik alanın Dirac denklemini üretir.
Bu sistem için global simetri aşağıdaki gibidir.
Burada ki gauge grubu U(1)dir. parçacık dönmeleriyle alanın faz açısının dönmeleri sabit θ ile belirlenir. Bu sistemin lokalleşmesinin anlamı θ ile θ(x) yer değiştirmesidir. Yaklaşık eş değişken türevi
Olağan elektrik yüküyle e yükünü belirler ve elektromanyetizmanın 4-vektör potensiyeliyle gauge alanını Langrangian etkileşimiyle sonuçlandırır.
Burada olağan 4 vektör elektrik yoğunluğudur. Sonuç olarak gauge prensibi minimal eşleşme olarak adlandırılan elektromanyetik alanın elektrik alan üretmesi gözlenir.
Gauge alan için Lagrangian eklenmesi diğer bir terimle elektrodinamik de aynı olan alan güç sensörü eklenmesiyle kuantum elektrodinamikteki başlangıc noktasını kullanarak Lagrangian elde edilir.
Matematiksel Formülleme
Gauge teorileri genellikle diferansiyel geometrinin dilinde tartışılmıştır. Matematiksel olarak, bir gauge bazı temel yığınların bir (yerel) bölümünde sadece bir seçimdir. Bir gauge dönüşümü sadece iki bölge arasındaki dönüşümdür.
Gauge teorisi bağlantıların çalışmasıyla (öncelikle yüksek enerjili fizikçiler tarafından çalışılmıştır.) hakim olmasına rağmen, bağlantı fikri genelde gauge teorisinin merkezi olmamıştır. Aslında, genel gauge teorisindeki bir sonuç gauge dönüşümlerinin temsillerini afine etmektedir. Örneğin afin modülleri. Bu temsiller belli özellikleri karşılayan jet paket bölümleri olarak sınıflandırılabilir. Bazı temsiller nokta tabanlı ( fizikçiler tarafından ilk tür gauge dönüşümleri için kullanılır) eşdeğişkenli olarak dönüşürler. Başka temsiller bağlantı formu ( fizikçiler tarafından ikinci tür gauge dönüşüm olarak adlandırılır.) şeklinde dönüşür. Diğer genel temsiller düz olmayan temsillerdir ancak bunlar çok karışıktır. Hala düz olmayan sigma modelleri düz olmayan bir şekilde dönüşür.
Eğer taban alanı uzay ya da uzayzaman ve yapı grubu Lie grup olan ana P demeti varsa, P formlarının bölümleri gauge dönüşüm gruplarınn homojen uzayının temelidir.
Bağlantılar (gauge bağlantısı) temel demetleri tanımlar. Bu demetler her vektor demetinde birleşmiş gevşek eşdeğişkenli türevlerdir. Eğer yerel bir çerçeve seçilmiş ise, eşdeğişkenli türev A bağlantı formu ile temsil edilir. Lie cebiri 1-form değerini vermiştir bu fizikte Gauge potensiyeli olarak anılır. Açıkça gerçek değildir ancak çerçeve niceliğe bağlıdır. Eğrilik formu F lie cebiri tarafından 2 değer formuna atanmıştır. Bu bağlantı formlarıyla kurulmuştur.
Burada d dışşal türevdir. dış cebiri temsiz eder.
Sonsuz derecede küçük gauge dönüşümleri Lie cebirini oluşturur. Lie cebri pürüzsüz skaler değerde olmasıyla karakterize edilir. Sonsuz derecede küçük gauge döüşümleri altında
eğer eşitliği olursa olur. Burada D eşdeğişken türevidir.
Ayrıca Buradaki eşdeğişkenli dönüşümlerdir.
Tüm gauge dönüşümleri genel olarak sonsuz dercede küçük gauge dönüşümleri tarafından oluşturulmuş olmayabilir. Baz manifoldu Lie grubu bu manifoldundan dönüşümlerin homotopi sınıf nontrivial şekilde sınır olmadan kompakt manifoldu olduğunda bir örnektir.
Yang-Mills hareketi şimdi bu formülle verilir. Formüldeki * Hodge Dual simgeler ve integral diferansiyel geometri olarak tanımlanır.
Gauge değişmeyen niceliği Wilson döngüsüdür. Bu döngü aşağıda görüldüğü üzere herhangi kapalı bir yol için γ tanımlanır.
Burada χ karmaşık temsili ρ karakteri ve emredilen operatör yolunu temsil eder.
Gauge Teorilerini Kuantumlama
Gauge teorileri herhangi kuantum alan teorisi için geçerli olan yöntemlerin uzmanlık ile kuantize olabilir. Ancak, gauge kısıtlamaları dayattığı inceliklerini nedeniyle diğer alan teorileri ortaya çıkmazsa çözülmesi gereken birçok teknik sorunlar var.Gauge teorileri zengin yapısı bazı hesaplamaların basitleştirilmesi sağlar. Örneğin, Farklı renormalizasyon sabitlerini Ward kimliklerine bağlamak gibi.
Yöntemler ve Amaçlar
Niceleme ilk olarak gauge teorisinde kuantum elektrodinamik (QED) idi. İlk yöntemler gauge yer sabitlemesi için geliştirildi ve daha sonra meşru kuantumlama için kullanıldı. Gupta-Bleuler yöntemi de bu sorunu ele almak geliştirilmiştir. Değişmeyen gauge teorileri artık çeşitli araçlarla tarafından ele alınır. Kuantumlamanın yöntemleri kuantumlama ile alakalı makalede bahsedilmektedir.
Teori tarafından izin verilen çeşitli işemler için kuantum genliklerinin hesaplanamaması kuantumlamanın ana noktası olmuştur. Teknik olarak vakum durumdaki belli korelasyon fonksiyonlarının hesaplamalarını azaltmak. Bu teorinin bir renormalizasyona içerir.
Teorinin çalışan eşleşmelerde yeteri kadar küçük olduğu zaman, bundan sonra gerekli tüm miktarlar pertürbasyon teoride hesaplanabilir. (Örneğin kanonik nicemleme gibi)Nicemleme şemaları bu tür hesaplamaları kolaylaştırmak için tasarlanmıştır. Nicemleme şemalarına pertürbatif nicemleme şemaları denebilir. Şu anda bu yöntemlerden bazıları gauge teorileri en hassas deneysel testlere öncülük ediyor.
Ancak, çoğu gauge teorilerinde çok fazla ilginç sorunlar bulunuyor. Niceleme şemaları bu problemlere uyum sağlıyor. sigara tedirgemesiz birçok ilginç soru vardır. (Örneğin kafes gauge teorisi gibi) bu sorunlara uygun niceleme düzenleri olmayan pertürbatif niceleme şemaları denebilir.Hassas hesaplamalar genellikle mükemmel hesaplama gerektirir ve bu nedenle dğier şemalara göre daha az gelişmiştir.
Anomaliler
Kuantum teorisi içerisinde klasik teorinin bazi simetrileri tutunamadı. Bu fenomen anormallik olarak adlandırıldı. En iyi bilinen anormalliklerden bazıları
- Ölçek anomali: Kuantum elektrodinamiğinde ölçek anomali Landau kutubuna neden olur. Kuantum Renkliğinde bu asimptotik serbestliğe yol açar
- Kiral anomal:: Bu anlık eğlimler yoluyola topoloji ile yanıdan bir bağlantısı vardır. Kuantum elektrodinamiğinde kiral anomali iki foton ve bir pion çürümesine neden olur.
- Gauge anomali: Bu anomali herhangi tutarlı fiziksel bir teoride iptal etmemiz gerekir. Elektro zayıf teoride bu iptal için gerekli olan elektronların ve kuarkların eşitliğidir.
Saf Gauge
Saf gauge, yani bir sıfır gauge-dönüşümüdür. Saf gauge elde etmek için gauge dönüşümünü boş bir alan üzerinde uygulamak gerekir. Yani alan yapılandırmanın uzayda belirli bir "gauge yörünge" sindedir.
Sonuç olarak, değişmeli durumda . Saf gauge bütün f(x) için alan yapılandırmaları olarak ayarlanır.
Ayrıca Bakınız
- Elektrozayıf kuvvet
- Lie cebiri
- Lie grubu
- Kuantum renk dinamiği
- Kuantum mekaniği
- Kuantum kütle çekimi
- Kuantum mekaniğinde simetri
- Simetri (fizik)
- Standart Model
- Kuantum Alan Kuramı Tarihi
- Kuantum elektrodinamiği
Bibliyografi
Genel Okuyucular
- Schumm, Bruce (2004) Deep Down Things. Johns Hopkins University Press. Esp. chpt. 8. A serious attempt by a physicist to explain gauge theory and the Standard Model with little formal mathematics.
Metinler
- Bromley, D.A. (2000). Gauge Theory of Weak Interactions. Springer. ISBN 3-540-67672-4.
- Cheng, T.-P.; Li, L.-F. (1983). Gauge Theory of Elementary Particle Physics. Oxford University Press. ISBN 0-19-851961-3.
- Frampton, P. (2008). Gauge Field Theories (3rd bas.). Wiley-VCH.
- Kane, G.L. (1987). Modern Elementary Particle Physics. Perseus Books. ISBN 0-201-11749-5.
Makaleler
- Becchi, C. (1997). "Introduction to Gauge Theories". arΧiv: hep-ph/9705211.
- Gross, D. (1992). "Gauge theory – Past, Present and Future". 23 Şubat 2016 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20160223060506/http://psroc.phys.ntu.edu.tw/cjp/download.php?type=paper&vol=30&num=7&page=955. Erişim tarihi: 2009-04-23.
- Jackson, J.D. (2002). "From Lorenz to Coulomb and other explicit gauge transformations". Am. J. Phys. 70 (9): 917–928. arXiv:physics/0204034. Bibcode 2002AmJPh..70..917J. DOI:10.1119/1.1491265.
- Svetlichny, George (1999). "Preparation for Gauge Theory". arΧiv: math-ph/9902027.
Dış Bağlantılar
- Hazewinkel, Michiel, ed. (2001), "Gauge transformation", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104, http://eom.springer.de/p/g043400.htm
- Yang–Mills equations on DispersiveWiki
- Gauge theories on Scholarpedia
- ↑ Wolfgang Pauli (1941). "Relativistic Field Theories of Elementary Particles," Rev. Mod. Phys. 13: 203–32.
- ↑ Pickering, A. (1984). Constructing Quarks. University of Chicago Press. ISBN 0-226-66799-5.
- ↑ J. J. Sakurai, Advanced Quantum Mechanics, Addison-Wesley, 1967, sect. 1–4.