Simpleks

Bir düzenli 3-simpleks veya dörtyüzlü

Geometri'de, bir simpleks (çoğulu simpleksler veya simplikler),üçgen gösteriminin bir genellemesi veya dörtyüzlü'nün boyutudur. Özel olarak, bir k-simpleks bir k-boyutlu politop'tur k + 1 köşeler dış-bükey'dir Daha formel olarak,k + 1 nokta ${\displaystyle u_{0},\dots ,u_{k}\in \mathbb {R} ^{k}}$ yardımıyla afin bağımsızdır,bunun anlamı${\displaystyle u_{1}-u_{0},\dots ,u_{k}-u_{0}}$ lineer bağımsızdır. öyleyse,bunlar tarafından belirlenen simpleks noktalar kümesidir ${\displaystyle C=\{\theta _{0}u_{0}+\dots +\theta _{k}u_{k}|\theta _{i}\geq 0,0\leq i\leq k,\sum _{i=0}^{k}\theta _{i}=1\}}$. örneğin, bir 2-tek-yönlü bir üçgendir, bir 3-simpleks bir dörtyüzlüdür, ve bir 4-simpleks 5-hücredir. Bir tek nokta belkide bir 0-simplekstir, ve bir doğru parçası belkide bir 1-simplekstir. Bir simpleks belkide verilen köşeleri içeren en küçük içbükey küme olarak tanımlanabilir .

Bir düzenli simpleks ^[1] bir simplekstir.Bu ayrıca bir düzenli politoptur.. Bir düzenli n-simpleksin inşası belkide bir düzenli(n − 1)-tekyönlü bağlantısıyla yeni bir köşe ortak köşe uzunluğu yardımıyla bütün orijinal köşelere yapılmaktadır.

topoloji'de ve kombinatorik'te,bu “ortak-yapışkan”a karşılık gelir, simplekslerin bu formu bir simpleks komplekstir.İlişkisel kombinatorik yapı soyut simpleks kompleks olarak adlandırılır, bu bağlamda “simpleks” kelimesi basit anlamda herhangi köşenin sonlu kümesidir. matematikte ve özellikle cebrik topoloji ve homoloji teorisi, bir Öklid simpleks Öklid uzayı içinde konveks kümenin özel bir tipidir.Bir üçgenin genelleştirme fikri, ve üçgenleştirme için kullanılıyor.

Öklidyen simpleks

Tanım

E³ içinde bir Öklid 3-simpleks.

Diyelimki y₀, y₁, …, y_k olsun doğrusal bağımsızlık Öklidyen n-uzay içindeki verilen bir nokta, Eⁿ olarak ifade edilir. Diyelimki S bir Eⁿ nin altkümesi ile verilen olsun

${\displaystyle S:=\left\{\sum _{i=0}^{k}\lambda _{i}{\mathbf {y}}_{i}:\lambda _{i}\geq 0\ {\text{ve}}\ \sum _{j=0}^{k}\lambda _{j}=1\right\}.}$

küme S bir Öklidyen k-simpleks denir,köşeler ile y₀, y₁, …, y_k, ve sıklıkla [y₀, y₁, …, y_k]. olarak ifade edilir.Verilen bir nokta y in S, λ_i verilen barisentrik koordinatlar olarak S.^[2]

Örnekler

• A Öklid 0-simpleks bir nokta'dır.
• A Öklid 1-simpleks bir çizgi segmenti 'dir.
• A Öklid 2-simpleks bir üçgen 'dir.
• A Öklid 3-simpleks bir dörtyüzlü 'dür.

Standard öklidyen simpleks

Standard Öklidyen k-simpleks, Δ_k ile adlandırılan E^k+1 nin bir alt kümesi olarak alınır ve [x₀, x₁ ile verilir …, x_k] burada x_i has bir 1 (i+1)^st içinde pozisyon ve bir başka her yerde sıfır var,^[2] yani

${\displaystyle {\mathbf {x}}_{i}=(\underbrace {0,\ldots ,0} _{i},1,\underbrace {0,\ldots ,0} _{k-i})\ \ {\text{tümü için}}\ 0\leq i\leq k.}$

Örnekler

• Δ₀ 1 E¹ içinde bir noktadır
• Δ₁ (1,0) ve (0,1) E²içinde birleştiren çizgi segmenti
• Δ₂ (1,0,0), (0,1,0) ve (0,0,1) in E³ içinde köşeleri ile üçgendir.
• Δ₃ (1,0,0,0), (0,1,0,0), (0,0,1,0) ve (0,0,0,1) E⁴içinde köşeler ile dörtyüzlüdür.

Yüzler

Verilen bir Öklidyen k-simpleks [y₀, y₁, …, y_k], Öklid p-simpleks ile köşeleri y₀, y₁, …, y_p − yani [y₀, y₁, …, y_p] −k-simpleks S 'in bir p-boyutlu yüzü denir .^[2] Simpleks ile köşeleri y_p+1, y_p+2, …, y_k − yani − [y₀, y₁, …, y_p].^[2] ya [y_p+1, y_p+2, …, y_k] nın ters yüzü denir. Bir öklidyen k-simpleks 0 dan k ya tüm boyutlarının yüzleri var.0-boyutlu yüzleri köşeler iken k-boyutlu yüz k-simpleksin kendisidir.

Örnekler

Standart Öklid düşünün 3-simpleks Δ₃.

• Δ₃ ün standart Öklid 3-simpleksi düşünün.Standart Öklid düşünün (1,0,0,0). Ters yüz bir 2-boyutlu bir yüzüdür; yani (standard olmayan)(0,1,0,0), (0,0,1,0) ve (0,0,0,1) köşeler ile üçgen tarafından verilen öklid 2-simplekstir.
• 1 boyutlu yüzlerin dörtyüzlü altı kenarları,birleştiren çizgi kesimi tarafından verilen 1-boyutlu yüz düşünün (0,1,0,0)'a (1,0,0,0).Ters yüz 1-boyutlu bir yüzüdür; yani (standard olmayan) Öklid 1-simpleks ile verilen çizgi segment kesimi (0,0,0,1)'e (0,0,1,0) .
• 2-boyutlu yüzlerin dörtyüzlü dört geleneksel üçgen yüzleri,köşeler ile üçgen tarafından verilen 2 boyutlu yüz düşünün.(1,0,0,0), (0,1,0,0) ve (0,0,1,0). Ters yüz 0-boyutlu bir yüzüdür; yani(non-standard olmayan) Öklid 0-simpleks ile (0,0,0,1) köşeleri.

n-simpleks

Elemanlar

n+1 noktanın herhangi boş olmayan küme dışbükey zarfı n-tek-yönlü olarak tanımlanır,bir simpleks yüz olarak adlandırılır. Yüzleri kendilerine tek-yönlüdür.özellikle, bir alt kümesinin dışbükey zarfının boyutu m+1 (n+1 tanımlama noktaları) m-simpleks olarak,n-simpleks m-yüz olarak adlandırılır. Bu 0-yüzler (i.e., kendine benzer Boyut-1 kümelerinin tanımlayıcı noktaları) köşe (yalın: köşe)dir,1-yüzleri denir,bu köşeler, bu (n − 1)-yüzlerine yüzleridir denir,ve bu tek n-yüzün bütünü n-kendisine simpleks denir. genel olarak,m-yüzlerinin sayısı binom katsayısına eşittir ${\displaystyle {\tbinom {n+1}{m+1}}}$. sonuç olarak, n-simpleks, m-yüzlerin sayısı olarak belkide Pascal üçgeni'nin ,(m + 1) sütunu (n + 1) satır bulunur.Bir simpleks A bir simpleks Bnin bir eş-yüzü ise B ,Anın bir yüzüdür. yüz ve yön bir simpleks kompleks'de tek-yönlü tipleri tanımlarken farklı anlamlara sahip olabilir.BakınızSimplektik kompleks#Tanımlar

Düzenli simpleks ailesi üç düzenli politop ailesinin ilkidir,Coxeter α_n in etiketi olarak,diğer iki çapraz-politop ailesi,β_netiketi olarak, vehiperküp, γ_nolarak etiketlenir.Dördüncü bir aile, hiperküpleri sonsuz mozaikleme,δ_n olarak etiketlenir.

1-yüzlerin (köşeler) sayısı n-simpleksin (n-1)inci üçgen numarası'dır,n-simpleks 2-yüzlerin numarası (n-2)inci tetrahedron numarasıdır, n-simpleks 3-yüzlerin numarası (n-3)cü 5-hücre numarasıdır,ve benzerleri.

n-Simpleks ögeler^[3]

Δ^n	Adı	Schläfli sembol Coxeter-Dynkin	0- yüzler (vertices)	1- yüzler (edges)	2- yüzler	3- yüzler	4- yüzler	5- yüzler	6- yüzler	7- yüzler	8- yüzler	9- yüzler	10- yüzler	Toplam yüz =2^n+1-1
Δ^0	0-simpleks (köşe)		1											1
Δ^1	1-simpleks (kenar)	{}	2	1										3
Δ^2	2-simpleks (üçgen)	{3}	3	3	1									7
Δ^3	3-simpleks (dörtyüzlü)	{3,3}	4	6	4	1								15
Δ^4	4-simpleks (5-hücre)	{3,3,3}	5	10	10	5	1							31
Δ^5	5-simpleks	{3,3,3,3}	6	15	20	15	6	1						63
Δ^6	6-simpleks	{3,3,3,3,3}	7	21	35	35	21	7	1					127
Δ^7	7-simpleks	{3,3,3,3,3,3}	8	28	56	70	56	28	8	1				255
Δ^8	8-simpleks	{3,3,3,3,3,3,3}	9	36	84	126	126	84	36	9	1			511
Δ^9	9-simpleks	{3,3,3,3,3,3,3,3}	10	45	120	210	252	210	120	45	10	1		1023
Δ^10	10-simpleks	{3,3,3,3,3,3,3,3,3}	11	55	165	330	462	462	330	165	55	11	1	2047

Yukarıdaki tabloda yüzleri sayısı Pascal üçgeni ile sol çapraz olmadan aynıdır.

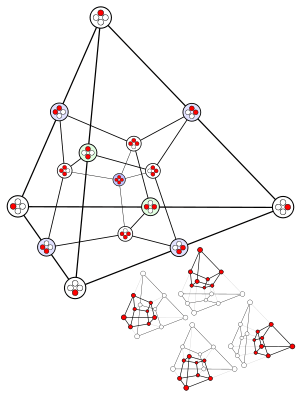Yüzlerin toplam sayısı, her zaman ikinin kuvveti eksi biridir. Bu rakam (hiperküp bir projeksiyon) dörtyüzlü 15 yüzlerin merkezlerini gösterir.

Bazı mutabakatlar,^[4] boş küme bir (−1)-simpleks olarak tanımlanır.Yukarıdaki simpleks eğer n = −1 ise hala mantıklıdır. Bu mutabakatlar cebirsel topoloji politop çalışması (örneğin simpleks homoloji gibi) uygulamalarında daha sık görülür.

Düzenli simpleks simetrik grafikler

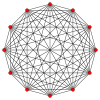
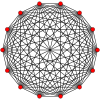
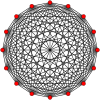
Petrie poligonu (çarpık ortogonal izdüşümler) bir daire üzerinde düzenli simpleks tüm köşeleri gösterir ve tüm tepe çiftleri kenarlarından bağlı

1	2	3	4	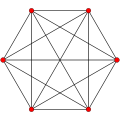5
6	7	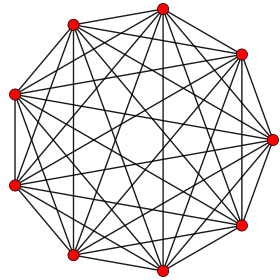8	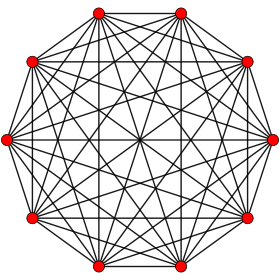9	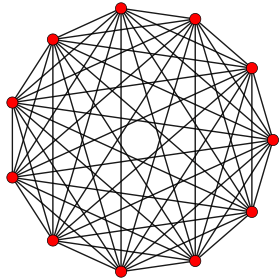10
11	12	13	14	15
16	17	18	19	20

Ayrıca bakınız

• Matematiksel şekillerin listesi
• Nedensel dinamik üçgenleştirme
• Uzunluk geometrisi
• Delaunay üçgenleştirme
• Tepe dörtyüzlü
• Diğer normal n-politop'lar
  • Hiperküp
  • Çapraz politop
  • dört boyutlu küp
• Politop
• Metcalfe Yasası
• Düzenli politopların bir listesi
• Schläfli dikşeması
• simpleksler algoritması - eşitsizlikler ile optimizasyon problemlerin çözümü için bir yöntem.
• simpleksler kompleksi
• simpleksler homolojisi
• simpleksler kümesi
• Üçlü plan
• 3-küre

Notlar

1. Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen  Chapter IV, five dimensional semiregular polytope
2. Wallace, Andrew H. (Jan 2009), Algebraic Topology: Homology & Cohomology, Dover Publications Inc., ISBN 0-486-46239-0 
3. "Sloane's A135278 : Pascal's triangle with its left-hand edge removed", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
4. Kozlov, Dimitry, Combinatorial Algebraic Topology, 2008, Springer-Verlag (Series: Algorithms and Computation in Mathematics)

Kaynakça

• Walter Rudin, Principles of Mathematical Analysis (Third Edition), (1976) McGraw-Hill, New York, ISBN 0-07-054235-X (See chapter 10 for a simple review of topological properties.).
• Andrew S. Tanenbaum, Computer Networks (4th Ed), (2003) Prentice Hall, ISBN 0-13-066102-3 (See 2.5.3).
• Luc Devroye, Non-Uniform Random Variate Generation. (1986) ISBN 0-387-96305-7; Web version freely downloadable.
• H.S.M. Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8
  • p120-121
  • p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n>=5)
• Eric W. Weisstein, Simplex (MathWorld)
• Stephen Boyd and Lieven Vandenberghe, Convex Optimization, (2004) Cambridge University Press, New York, NY, USA.

Dış bağlantılar

• Şablon:GlossaryForHyperspace

Şablon:Dimension topics Şablon:Polytopes