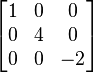Köşegen matris

Doğrusal cebirde köşegen matris, (↘) ilkköşegenin dışında kalan girişlerin tümü sıfır ve genellikle kare matris olan bir matrisdir. n sütun ve n satırdan oluşan D = (d_i,j) matrisi şöyledir:

$i \ne j\ \forall i,j \in \{1, 2, \ldots, n\}\mbox{ ise } d_{i,j} = 0 \mbox{ olur }$,

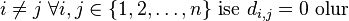Örneğin, aşağıdaki matris köşegendir:

$\begin{bmatrix} 1 & 0 & 0\\ 0 & 4 & 0\\ 0 & 0 & -2\end{bmatrix}$

Köşegen matris yerine bazen dikdörtgen köşegen matris de denir. Burada mxn matrisi, d_i,i formundaki girişlere sahiptir. Örneğin;

$\begin{bmatrix} 1 & 0 & 0\\ 0 & 4 & 0\\ 0 & 0 & -3\\ 0 & 0 & 0\\ \end{bmatrix}$ veya $\begin{bmatrix} 1 & 0 & 0 & 0 & 0\\ 0 & 4 & 0& 0 & 0\\ 0 & 0 & -3& 0 & 0\end{bmatrix}$

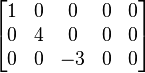
Ayrıca bu maddenin dışında kalanlar yalnızca kare matris olarak anılır. Her kare köşegen matris de, bir simetrik matrisdir. Ayrıca girişler eğer R veya C alanında ise, normal matrisdir. Bir köşegen matrisi, üst ve alt üçgen matris olarak da tanımlayabiliriz. I_n birim matris ve sıfır matris de köşegendir. Bir boyutlu matrisler de daima köşegendir.