Lie süpercebiri
matematik'te, bir Lie supercebri bir Lie cebri genelleştirilmesi Z2-sınıflandırma içerir. Lie supercebri teorik fizik'te önemlidir.süpersimetri'nin matematiği kavramında kullanılıyor. Bu teorilerin çoğunda, supercebirin çift ögesi bozon'a ve tek ögesi fermiyon'a (ama bu her zaman doğru değildir; örneğin,BRST süpersimetride tersidir)karşılık gelmektedir
Tanım
biçimsel olarak,bir Lie süpercebri bir (birleşmeli olmayan) Z2-kademeli cebridir, veya,değişmeli halka üzerinde bir süpercebir(tipik olanı R veya C) olan çarpım [·, ·], Lie süperbraket veya süperdeğişmeli olarak adlandırılır, iki koşulu karşılayan (olağan analoglarının Lie cebri aksiyomları, ile kademeli):
Süper çarpık-simetri:
süper Jacobi özdeşliği:
burada x, y, ve z saf Z2-seviyesi içindedir.Burada , |x| ifadesi x ın derecesi (ya da 0 veya 1). derecesi [x,y]'nin derecesi,x ve y modulo 2'nin derecelerinin toplamıdır.
sahip oldukları teorem için gerekli koşullar ![[x,x]=0](../I/m/15d5c6c9d48c5f1887e99d323c2e9bf8.png) için |x|=0 (eğer 2 tersi ise bu otomatik olarak aşağıdakidir) ve
için |x|=0 (eğer 2 tersi ise bu otomatik olarak aşağıdakidir) ve
![[[x,x],x]=0](../I/m/5ef17fb88fd0486d692a85350d2815dd.png) için |x|=1 (eğer 3 tersi ise bu otomatik olarak aşağıdakidir).Zemin halka tamsayılar veya Lie süpercebri bir serbest modüldür, Bu koşullar durumunda Poincaré-Birkhoff-Witt Teoremi'ne eşdeğerdir(ve, genel olarak, bunlar sahip olmak için teoreme gerekli olan koşullar).
için |x|=1 (eğer 3 tersi ise bu otomatik olarak aşağıdakidir).Zemin halka tamsayılar veya Lie süpercebri bir serbest modüldür, Bu koşullar durumunda Poincaré-Birkhoff-Witt Teoremi'ne eşdeğerdir(ve, genel olarak, bunlar sahip olmak için teoreme gerekli olan koşullar).
sadece Lie cebri için,Lie süpercebrinin Evrensel zarflama cebiri bir Hopf cebri yapısı verebilir.
Derecelendirilmiş Lie cebrinde ayırım
Bir derecelendirilmiş Lie cebri (söylenişi, Z veya N ile derecelendirme) bu derecelendirme içinde karşıt-değişmeli ve Jacobi anlamda bir 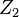 derecelendirme vardır (çift ve tek parçaları içinde cebrik "yuvarlama" denir ), ama "süper" olarak anılmaz.
Bkz. dikkat;dereceli Lie cebri ders için.
derecelendirme vardır (çift ve tek parçaları içinde cebrik "yuvarlama" denir ), ama "süper" olarak anılmaz.
Bkz. dikkat;dereceli Lie cebri ders için.
Tek ve çift parça
Burda çift altcebir yani bir Lie süpercebir formunun çift altcebrinde bir (normal) Lie cebrinin bütün işaretleri yoktur ve süperbraket bir normal Lie brakete uymaz,bu gözden kaçırılmamalıdır
Bir Lie supercebri hakkında düşünülecek tek çift ve tek parçalarının, L0 and L1 ayrı ayrı dikkate almaktır. Eğer, L0 bir Lie cebri, L1 dir L0,ın bir lineer gösterim'i ve burada bir simetrik L0-eşdeğer lineer haritalama varsa  öyleki L1'deki bütün x,y ve için
öyleki L1'deki bütün x,y ve için
İçe dönme
Bir * Lie supercebri bir karmaşık Lie supercebri içedönük doğrusal olmayan haritalama ile kendisinden kendisine Z2 nin sıralamasının dereceleme ve uygunluğu ile donatılmıştır [x,y]*=[y*,x*] Lie supercebri içindeki tüm x ve y için. (Bazı yazarlar [x,y]*=(−1)|x||y|[y*,x*] tercihi için hemfikirdirler; * −* a değişim iki anlaşma arasında anahtardır.) Bu evrensel zarf cebri bir olağan*-cebridir.
Sınıflandırma
sade karmaşık sonlu boyutlu Lie supercebri Victor Kac tarafından sınıflandırılmıştı.
Temel klasik tıkız Lie supercebri (bu Lie cebri değil) şudur:
SU(m/n) burada süperbirim Lie cebri değişmezleri:
Bu iki ortosimplektik (bkz. aşağıda) değişmezleri verip,eğer mz değişkenleri alırsak ve nw değişkenleri olmayan değişmeli olmayan ve gerçek ve sanal kısımları alır. Bu nedenle şu var
SU(n/n)/U(1)Biz cebir basit yapmak için bir U(1) jeneratörünü kaldırmak superbirimli Lie cebirlerinin özel bir durumudur.
OSp(m/2n) Bu ortosimplektik gruplardır.Bunlar tarafından verilen değişmezler var:
m değişmeli değişkeni (x) ve karşıt-değişmeli değişkeni(y,z)'nin birçift n'i içindir .Bu superçekim teorisi içinde önemli bir simetridir.
D(2/1;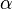 ) Bu
) Bu 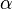 değişkenleri tarafından parametrize supercebrin bir kümesidir.17 boyutludur ve OSp(9|8)nin bir alt cebridir. gurubun birkaç kısmıO(3)xO(3)xO(3) dır.Bu yüzden aşağıdaki değişmezleri vardır:
değişkenleri tarafından parametrize supercebrin bir kümesidir.17 boyutludur ve OSp(9|8)nin bir alt cebridir. gurubun birkaç kısmıO(3)xO(3)xO(3) dır.Bu yüzden aşağıdaki değişmezleri vardır:
belirli bir sabit için 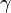 .
.
F(4) OSp(24|16)'un bu olağanüstü Lie superalcebrinin boyutu 40 ve bir alt cebirdir. Grubun birkaç bölümü O(3)xSO(7) olur, böylece üç değişmezleri şudur:
Bu grup iki bileşenli oktonyon spinörleri olarak 16 bileşeni spinörleri dikkate alınarak oktonyon ile ilgilidir.Ve gamma matrisler birimi oktonyon olarak üst endeksleri etkiler
Dahası var 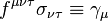 burada f oktonyon çarpma yapısı sabittir .
burada f oktonyon çarpma yapısı sabittir .
G(3) Bu olağanüstü Lie supercebri 31 boyutu olan ve bir alt cebiridir OSp(17|14). Grubun birkaç bölümü O(3)xG2 dir. ilk sabit yani değişmezler yukarıdakine benzer:
burada da adlandırılan iki tanesi tuhaf serisi olarak adlandırılan p(n) ve q(n).
Sonsuz Boyutlu Basit Lineer Kompakt Lie Supercebri sınıflandırılması
10 serinin uygun sınıflandırması W(m, n), S(m, n) ((m, n) ≠ (1, 1)), H(2m, n), K(2m+1, n), HO(m,m) (m ≥ 2), SHO(m,m) (m ≥ 3), KO(m,m + 1), SKO(m,m + 1; β) (m ≥ 2), SHO∼(2m,2m), SKO∼(2m+1,2m + 3) ve 5 olağanüstü cebiri:
- E(1,6), E(5,10), E(4,4), E(3,6), E(3,8)
Bunların standart model ölçü grubu var çünkü son iki (Kac'a göre) özellikle ilginçSU(3)xSU(2)xU(1) kendi sıfır düzeyi cebri gibi. Sonsuz boyutlu (afin) Lie supercebri önemli bir simetrisi olan süpersicim teorisi'dir
Kategori-teorik tanım
kategori teorisi içinde, bir Lie süpercebri ilişkisel olmayan süpercebir olarak tanımlanabilir aşağıdaki çarpımları karşılar
where σ is the cyclic permutation braiding  . In diagrammatic form:
. In diagrammatic form:
Ayrıca bakınız
- Anyonik Lie cebiri
- Grassmann cebri
- Bir Lie süpercebrinin gösterimi
- Süperuzay
- Süpergrup
Kaynakça
- Kac, V. G. Lie superalgebras. Advances in Math. 26 (1977), no. 1, 8--96.
- Manin, Yuri I. Gauge field theory and complex geometry. Grundlehren der Mathematischen Wissenschaften, 289. Springer-Verlag, Berlin, 1997. ISBN 3-540-61378-1
- Pavel Grozman, Dimitry Leites and Irina Shchepochkina. "LIE SUPERALGEBRAS OF STRING THEORIES"
![[x,y]=-(-1)^{|x| |y|}[y,x].\](../I/m/77d7c476420482cd567dbc5dd9296e83.png)
![[x,[y,z]]=[[x,y],z]+(-1)^{|x| |y|}[y,[x,z]]\](../I/m/e6f9f79244d44ee4cc7e6da64d858ac8.png)
![\left\{x, y\right\}[z]+\left\{y, z\right\}[x]+\left\{z, x\right\}[y]=0.](../I/m/6d632b99e090a5da0d9e37e859d88286.png)
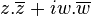
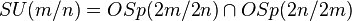

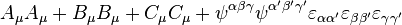

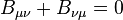
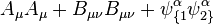


![[\cdot,\cdot]\circ (id+\tau_{A,A})=0](../I/m/78cb0b06209d4439c79640e4af2ea16c.png)
![[\cdot,\cdot]\circ ([\cdot,\cdot]\otimes id)\circ(id+\sigma+\sigma^2)=0](../I/m/139a09551ed2b88681de0ee18cd67fc4.png)
