Monty Hall problemi

Bu sayfa, başka dilde bir Vikipedi'den çevrilmektedir. Siz de yardım etmek istiyorsanız veya çeviri yarıda kalmışsa, çalışmaya katılan kişilerle veya çeviri grubu ile iletişime geçip, sayfanın durumunu onlara sorabilirsiniz. Sayfanın geçmişine baktığınızda, sayfa üzerinde çalışma yapanları görebilirsiniz.

Arabayı ararken yarışmacı kapılardan birini, diyelim ki 1'inciyi seçmiş olsun. Sunucu diğer kapılardan birini, diyelim ki 3'ü açar ve arkasında keçi vardır; yarışmacıya 1. kapı yerine 2'nciyi seçebileceğini söyler.

Monty Hall problemi, Amerikan TV yarışma programı Let's Make a Deal'a dayanan bir olasılık bulmacasıdır. Problem adını, yarışmanın sunucusu Monty Hall'dan alır. İçinde bir paradoksu da barındırması nedeniyle Monty Hall paradoksu olarak da anılan problemin sonucu saçma görünmekle birlikte, ispatlanabilir ve doğrudur.

Problemin iyi bilinen bir açıklaması Parade dergisinde yayımlandı:

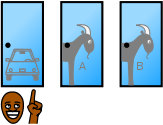
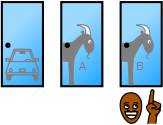
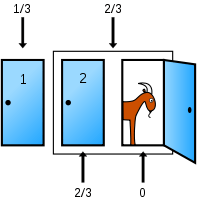
Bir yarışma programında olduğunuzu ve üç kapıdan birini seçme hakkınız olduğunu varsayalım. Kapılardan birinin ardında bir araba, diğerlerinin ardında ise keçiler var. Kapılardan birini, diyelim ki 1'inciyi seçiyorsunuz ve kapıların ardında ne olduğunu bilen sunucu, diğer kapılardan birini, diyelim ki ardında keçi olan 3'üncüyü açıyor. Daha sonra size soruyor: "2. kapıyı seçmek ister misiniz?" Seçiminizi değiştirmek sizin yararınıza mıdır? (Whitaker 1990)

Yarışmacı geriye kalan iki kapıdan hangisinin kazanan olduğundan emin olamadığı için, çoğu kişi bu kapıların eşit olasılığa sahip olduğunu ve seçimi değiştirmenin hiçbir şeyi değiştirmeyeceğini sanır. Aslında, problemin klasik açıklamasına göre yarışmacı seçimini değiştirmelidir. Zira böylece arabayı bulma olasılığını 1/3'ten 2/3'e çıkarır; yani ikiye katlar.

Problemin yukarıdaki açıklaması ve çözümü Parade'de yer aldığı zaman, aralarında doktora derecesi olan yaklaşık bin kişinin bulunduğu on bin okur, dergiye yazarak çözümün yanlış olduğunu iddia etti. Bazı eleştirmenler problemin Parade versiyonunda sunucunun davranışının belli açılardan iyi şekilde açıklanmadığını; örneğin sunucunun bir kapıyı açıp böyle bir öneri yapıp yapamayacağının bilinmediğini belirtti. Öte yandan, bu gibi olası davranışların söz konusu tartışmayla bir ilgisi yoktur ya da probleme etkisi çok azdır (vos Savant 1990) ve bu davranış yazar tarafından açıkça belirtilmiştir (Seymann 1991). Problemin daha genel yorumları, örneğin bazı durumlarda sunucunun ardında araba olan kapıyı açabileceği, matematik eserlerinde tartışılmıştır.

Monty Hall problemi, yaygın biçimlerinden biriyle, daha eski bir problem olan Üç Mahkum Problemine matematiksel olarak eşittir ve bunların ikisi birden daha da eski olan Bertrand'ın kutusu paradoksuyla benzerlikler gösterir. Bunlar ve olasılığın eşit olmayan şekilde dağıtımıyla ilgili diğer problemlerin doğru şekilde çözümünün zor olduğu yönünde bir inanış vardır ve bu durum problemlerin nasıl algılandığını ele alan psikolojik çalışmaların yapılmasına yol açmıştır. Monty Hall probleminin tamamıyla açık çözümüyle buna ilişkin açıklamalar, benzetme ve resmi matematiksel kanıtlar ortaya konulduğunda bile, çoğu kişi doğru yanıta şüpheyle bakmaktadır.

Problem

Steve Selvin 1975'te American Statistician'a bir mektup yazarak kabaca yarışma programı Let's Make a Deal'a dayanan bir problemi anlattı. Daha sonraki bir mektubunda buna "Monty Hall problemi" adını verdi (Selvin 1975b). Matematiksel formulasyonlarından birinde (ki buna şartlı versiyon denilir, aşağıya bakınız), problem Martin Gardner'ın 1959'da Scientific American'daki köşesi Mathematical Games'te açıkladığı (Gardner 1959a) Üç Mahkum Problemine matematiksel olarak eşittir (Morgan et al., 1991).

Selvin'in Monty Hall problemi iyi bilinen haliyle, Marilyn vos Savant'ın Parade dergisindeki Ask Marilyn köşesinde yayımlanan bir mektupla yeniden gündeme geldi:

Bir yarışma programında olduğunuzu ve üç kapıdan birini seçme hakkınız olduğunu varsayalım. Kapılardan birinin ardında bir araba, diğerlerinin ardında ise keçiler var. Kapılardan birini, diyelim ki 1'inciyi seçiyorsunuz ve kapıların ardında ne olduğunu bilen sunucu, diğer kapılardan birini, diyelim ki ardında keçi olan 3'üncüyü açıyor. Daha sonra size soruyor: "2. kapıyı seçmek ister misiniz?" Seçiminizi değiştirmek sizin yararınıza mıdır? (Whitaker 1990)

Problemin bu formulasyonunda bazı belirsizlikler vardır: Sunucunun her zaman bir başka kapıyı açıp açmayacağı, her zaman bir kapı değiştirme önerisi getirip getirmeyeceği ya da ardında araba bulunan kapıyı açıp açmayacağı net değildir (Mueser and Granberg 1999). Öte yandan, yaygın yoruma göre, sunucunun her zaman ardında keçi olan bir kapıyı açmak ve kapı değiştirme önerisinde bulunmak zorunda olduğu ve yarışmacının ilk seçiminin 1/3 olasılıkla doğru olduğu kabul edilir. Ayrıca yarışmacının ilk seçimi ardında araba olan kapı ise, sunucunun kalan iki kapıdan birini tamamen rastgele açacağı çoğunlukla kabul edilir (Barbeau 2000:87).

Soruyu soranın kesin niyetini açıkça anlamadan, herhangi bir problemin tek bir doğru çözümü bile olamaz (Seymann 1991). İnsanların genellikle algıladığı matematiksel olarak açık sorunun formulasyonu, Krauss ile Wang'e göre şöyledir (2003:10):

Bir yarışma programında olduğunuzu ve üç kapıdan birini seçme hakkınız olduğunu varsayalım. Kapılardan birinin ardında bir araba, diğerlerinin ardında ise keçiler var. Yarışmanın kuralları şunlar: Siz kapıyı seçtikten sonra, kapı hemen açılmaz. Kapıların ardında ne olduğunu bilen sunucu Monty Hall, şimdi geriye kalan iki kapıdan birini açmak zorundadır ve açacağı kapının ardında mutlaka bir keçi olacaktır. Eğer geriye kalan iki kapının ardında da keçi varsa, kapılardan birini rastgele seçecektir. Monty Hall ardında keçi olan kapıyı açtıktan sonra, size ilk seçiminizi değiştirip kalan kapılardan diğerini seçmek isteyip istemediğinizi soracaktır. Düşünün ki Kapı 1'i seçtiniz ve sunucu ardında keçi olan Kapı 3'ü açtı. Daha sonra size "Seçiminizi 2 numaralı kapıdan yana değiştirmek ister misiniz?" diye sordu. Seçiminizi değiştirmek sizin yararınıza mıdır? (Krauss and Wang 2003:10)

Ayrıca, yarışmacı için arabayı kazanmanın keçiyi kazanmaya göre daha tercih edilir olduğunu varsaymamız gerekir.

Popüler çözüm

Yarışmacı kapılardan birini seçtiğinde, seçilen kapının ardında araba olma olasılığı 1/3'tür ve araba 2/3 olasılıkla diğer kapılardan birinin ardındadır. Sunucunun ardında keçi olan bir kapıyı açması, yarışmacıya seçtiği kapının ardında ne olduğuyla ilgili yeni bir bilgi vermez. O kapının ardında araba olma olasılığı hâlâ 1/3'tür. Sunucunun verdiği yeni bilgi, açılan kapının ardında araba olma olasılığının 0/3 olduğudur. Dolayısıyla araba 2/3 olasılıkla hâlâ açılmayan kapının ardındadır (Wheeler 1991; Schwager 1994). Kapı seçimi değiştirilirse arabayı kazanma olasılığı 2/3'tür, bu nedenle yarışmacı seçimini değiştirmelidir (Wheeler 1991; Mack 1992; Schwager 1994; vos Savant 1996:8; Martin 2002).

Bu popüler hikâyeyi matematiksel olarak kesin bir çözüme kavuştururken, 2. ya da 3. kapıyı açmanın 1. kapının ardında araba olma olasılığını neden değiştirmediği sorulabilir. Bu soru, simetriye başvurularak yanıtlanabilir: Yukarıda yapılan varsayımlar ışığında, kapılar rastgele yeniden numaralandırılırsa ve özellikle 2 ile 3 yer değiştirirse, değişen bir şey olmaz. Dolayısıyla, arabanın 1. kapının ardında olması, yarışmacının 1'i seçmesi ve Monty'nin 2'yi açması şartlı olasılığı, yine arabanın 1. kapının ardında olması, yarışmacının 1'i seçmesi ve Monty'nin 3'ü açması şartlı olasılığına eşittir. Bu iki (eşit) olasılığın ortalaması 1/3'tür, bundan dolayı her birinin olasılığı da ayrı ayrı 1/3'tür.

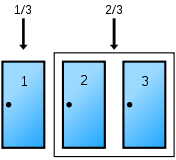
Analiz, yarışmacının başlangıçta arabayı, keçi A'yı ya da keçi B'yi seçmesi eşit olasılıklarına göre örneklendirilerek açıklanabilir (Economist 1999):

1. Sunucu iki keçiden birini açar. Yarışmacı arabayı seçmiştir. (olasılık: 1/3) Karar değiştirmek kaybettirir. 2. Sunucu B keçisini açmak zorunda kalır. Yarışmacı A keçisini seçmiştir. (olasılık: 1/3) Karar değiştirmek kazandırır. 3. Sunucu A keçisini açmak zorunda kalır. Yarışmacı B keçisini seçmiştir. (olasılık: 1/3) Karar değiştirmek kazandırır.

Yarışmacının ilk tercihinde arabayı, A keçisini ya da B keçisini seçme ihtimali eşittir. Bu durumda karar değiştirmek, 2/3 ihtimalle kazandırır.

Yukarıdaki diyagram seçimini değiştiren bir yarışmacının her zaman ilk seçiminin tam tersini elde edeceğini gösterir ve bu seçimin keçi olma olasılığı araba olma olasılığının iki katı olduğundan, seçimi değiştirmek her zaman avantajlıdır. Diğer deyişle, önce keçiyi seçmiş olma olasılığı 2/3, arabayı seçmiş olma olasılığı ise 1/3'tür. Monty Hall artık "keçili kapıyı" ortadan kaldırdıktan sonra, baştan ardında keçi olan kapıyı seçmiş olan yarışmacının arabayı kazanması, baştan ardında araba olan kapıyı seçmiş olan yarışmacının ise keçiyi "kazanması" gerekir. Yarışmacının baştan keçiyi seçmiş olma olaslığı 2/3 olduğundan, seçimi değiştirmek her zaman yararına olacaktır.

Diğer iki kapının şansı 2/3 iken, yarışmacının seçtiği kapının şansı 1/3'tür.

Yarışmacının seçtiği kapının şansı 1/3, diğer iki kapının şansı 2/3. Bu 2/3'lik şans, hâlâ açılmamış olan kapınınki 2/3 ve sunucunun açtığı kapınınki 0 olmak üzere paylaştırılır.

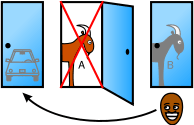
Çözümü anlamanın bir başka yolu, en baştaki seçilmemiş iki kapıyı birlikte değerlendirmektir. Bir kapının açılıp kaybedilen kapı olarak gösterilmesi yerine, buna eşit bir işlem olarak (açılmış olan kapı seçilemeyeceğinden) seçilmemiş olan iki kapı tek bir olarak düşünülebilir. (Adams 1990; Devlin 2003; Williams 2004; Stibel et al., 2008).

Cecil Adams'ın ifade ettiği gibi (Adams 1990), "Monty aslında şunu söylemektedir: Seçtiğiniz kapıda ısrar edebilir ya da diğer iki kapıya sahip olabilirsiniz." Yarışmacı bu durumda ilk seçimini korumak ya da iki kapının ardındakilerin toplamını seçmek hakkına sahiptir. Zira 2/3'lük arabayı saklama şansı, bu kapılardan birinin açılmasıyla değişmiş olmaz.

Keith Devlin'in sözleriyle (Devlin 2003), "Kapıyı açarak Monty yarışmacıya şunu söylemektedir: 'Seçmediğiniz iki kapı var ve ödülün bunlardan birinin ardında olma olasılığı 2/3. Ödülün nerede olduğunu bildiğimden bu iki kapıdan birini açarak ardında ödül bulunmadığını gösterecek ve size yardım edeceğim. Artık bu ek bilgiden yararlanabilirsiniz. Seçtiğiniz A kapısı 3'te 1 olasılıkla kazanandır. Bunu değiştirmiş olmuyorum. Ancak C'yi eleyerek size, B'nin 3'te 2 olasılıkla ödülü sakladığını göstermiş oluyorum.'"

Olasılık yoluyla çözüm

Morgan ve diğerleri (1991) popüler çözümlerin çoğunun, Whitaker'ın Kapı 1'i seçen ve sunucunun Kapı 3'ü açtığını gören yarışmacıya ilişkin özgün sorusunu (Seymann) açıkça ele almadıkları için eksik olduğunu belirtti. Bu çözümler seçimini değiştiren tüm yarışmacılar için kazanma olasılığının 2/3 olduğunu doğru şekilde gösterir. Ancak belli varsayımlar yapılmaksızın bu, seçimin değiştirilmesiyle kazanma olasılığının mutlaka 2/3 olacağı anlamına gelmez. Bu olasılık, bir koşullu olasılıktır (Morgan et al. 1991; Gillman 1992; Grinstead and Snell 2006:137; Gill 2009b). Aradaki fark, analizin yarışmacının ilk seçimi ile sunucunun açtığı kapının toplam olası kombinasyonlarına göre ortalama olasılığına mı, yoksa yalnızca yarışmacının Kapı 1'i seçtiği ve sunucunun Kapı 3'ü açtığı belirli tek bir duruma mı dayandığına bağlıdır. Farkı açıklamanın bir diğer yolu da, yarışmacının seçimini değiştirmeye sunucu bir kapıyı açmadan önce karar vermek zorunda mı olduğu, yoksa sunucunun hangi kapıyı açtığını gördükten sonra karar vermesine izin verilip verilmediğine ilişkindir (Gillman 1992). Yukarıda kesin olarak belirtilen problem açıklaması için bu iki olasılık da 2/3 olmasına karşın, koşullu olasılık, toplam olasılığa ve bunlardan birinin ya da ikisinin birden problemin tam formulasyonuna bağlı olarak saptanıp saptanamayacağına göre değişebilir (Gill 2009b).

Yarışmacının 1. kapıyı seçmesi hâlinde tüm olası sonuçları ve bunların gerçekleşme ihtimallerini gösteren karar ağacı

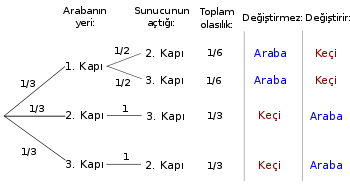
Sunucunun hangi kapıyı açtığını bilerek seçimi değiştirme sonucunda kazanmanın koşullu olasılığı, aşağıdaki genişletilmiş tabloya ya da aynı olasılıkları gösteren yandaki seçim ağacına başvurularak (Chun 1991; Grinstead and Snell 2006:137-138) veya aşağıdaki matematiksel formulasyon bölümüne bakılarak saptanabilir. Örneğin, sunucu Kapı 3'ü açar ve yarışmacı seçimini değiştirirse, yarışmacı, eğer araba Kapı 2'nin arkasındaysa 1/3 olasılıkla kazanır ve araba Kapı 1'in arkasındaysa 1/6 olasılıkla kaybeder. Sunucunun Kapı 2'yi açmasına bağlı olasılıklar bu hesaba dahil değildir. Bu koşullu olasılıkları dönüştürmek için, bunlar toplamlarına bölünür. Böylece yarışmacı Kapı 1'i seçtiği ve sunucu Kapı 3'ü açtığında kazanmanın koşullu olasılığı (1/3)/(1/3 + 1/6), yani 2/3'tür. Bu çözüm, problemde sunucunun kapılardan birini rastgele açmaya, yarışmacının ilk seçimini yapmasından sonra karar vereceğine ilişkin sınırlamaya bağlıdır.

Araba 3. kapının ardında	Araba 1. kapının ardında		Araba 2. kapının ardında
Oyuncunun ilk tercihi 1. kapı
Sunucu 2. kapıyı açmak zorunda	Sunucu ardında keçi olan kapılardan herhangi birini rastgele açar		Sunucu 3. kapıyı açmak zorunda
1/3 olasılık	1/6 olasılık	1/6 olasılık	1/3 olasılık
Tercih değiştirmek kazandırır	Tercih değiştirmek kaybettirir	Tercih değiştirmek kaybettirir	Tercih değiştirmek kazandırır
Sunucu 2. kapıyı açarsa, karar değiştirme durumundaki kazanma ihtimali, karar değiştirmeme durumunun iki katıdır		Sunucu 3. kapıyı açarsa, karar değiştirme durumundaki kazanma ihtimali, karar değiştirmeme durumunun iki katıdır

Matematiksel formulasyon

Yukarıdaki çözüm Gill, 2002, Henze, 1997 ve başka birçok ismin yaptığı gibi Bayes teoremi kullanılarak ispatlanabilir. Farklı yazarlar tarafından çeşitli gösterimler kullanılmış olsa da, aşağıda anlatılan versiyon karakteristik çözüm olarak kabul edilebilir. Ayrık rastlantı değişkenleri düşünelim:

${\displaystyle A\in \{1,2,3\}}$: Arabanın bulunduğu kapının numarası,

${\displaystyle Y\in \{1,2,3\}}$: Yarışmacının seçtiği kapı

${\displaystyle H\in \{1,2,3\}}$: Host'un (Sunucunun) açtığı kapı.

Araba kapıların arkasına rastgele yerleştirildiğinden, bütün A değerleri için şartlar eşittir. Buna göre A'nın başlangıç (koşulsuz) olasılığı

${\displaystyle P(A)\,={\tfrac {1}{3}}}$, her A değeri için.

Ayrıca, yarışmacının başlangıçtaki seçimi arabanın konulmasından bağımsız olduğundan, A ve Y değişkenleri bağımsızdır. Dolayısıyla bir Y değeri için A'nın koşullu olasılığı

${\displaystyle P(A|Y)\,=P(A)}$, A ve Y'nin bütün değerleri için.

Sunucunun seçimi A ve Y değerlerine göre H'nin koşullu olasılığı ile gösterilir:

${\displaystyle P(H|A,Y)\,\,=\,{\begin{cases}\,\\\,\\\,\\\,\end{cases}}}$	${\displaystyle \,0\,}$		eğer H = Y, (sunucu yarışmacının seçtiği kapıyı açamaz)
	${\displaystyle \,0\,}$		eğer H = A, (sunucu arabanın bulunduğu kapıyı açamaz)
	${\displaystyle \,1/2\,}$		eğer Y = A, (arkasında araba olmayan kapıların açılması eşit ihtimallidir)
	${\displaystyle \,1\,}$		eğer H ${\displaystyle \neq }$A ve Y ${\displaystyle \neq }$ A, (açılabilecek sadece bir kapı vardır)

Sunucu kapılardan birini açtıktan sonra, yarışmacı Bayes kuralını kullanarak kapıların herhangi biri arkasında arabanın bulunması olasılığını hesaplayabilir. Değer, seçilen H ve Y değerlerine bağlı A'nın koşullu olasılığıdır:

${\displaystyle P(A|H,Y)\,={\frac {P(H|A,Y)P(A|Y)}{P(H|Y)}}}$,

bu oranda payda marjinal (bileşen) olasılığı gösterir

${\displaystyle P(H|Y)\,=\sum _{A=1}^{3}P(H,A|Y)=\sum _{A=1}^{3}P(H|A,Y)P(A|Y)}$.

Dolayısıyla, eğer yarışmacı 1. kapıyı seçer ve sunucu 3. kapıyı açarsa, seçilen kapının değiştirilmesi halinde kazanma olasılığı

${\displaystyle P(A=2|Y=1,H=3)={\frac {1\times {\frac {1}{3}}}{{\frac {1}{2}}\times {\frac {1}{3}}+1\times {\frac {1}{3}}+0\times {\frac {1}{3}}}}={\tfrac {2}{3}}.}$

Kafa karışıklığının kaynakları

Monty Hall problemi ilk açıklandığı zaman insanların büyük çoğunluğu tüm kapıların eşit olasılıkta olduğunu ve kapı değiştirmenin önemli olmadığını düşünmekteydi (Mueser and Granberg, 1999). Yapılan bir çalışmada 228 denekten yalnızca %13'ü kapı değiştirmeyi seçti (Granberg and Brown, 1995:713). The Power of Logical Thinking isimli kitabında vos Savant (1996:15) bilişsel psikolog Massimo Piattelli-Palmarini'nin "... tarihte diğer hiçbir istatistiksel bulmaca insanları kandırmaya bu kadar yaklaşmadı" ve "Nobel Ödüllü fizikçiler bile bu probleme sistematik şekilde yanlış cevap verir ve bunda ısrar eder. Ayrıca doğru yanıtı verenleri basılı bir eserle paylamaya hazırdırlar." sözleri ile bu durumu anlattı.

Problemin çoğu açıklaması, özellikle de Parade Magazine'deki, asıl yarışma programının kurallarına uymaz (Krauss and Wang, 2003:9) ve sunucunun davranışını ya da arabanın yerinin rastgele seçildiğini açıkça belirtmez (Granberg and Brown, 1995:712). Krauss ve Wang, insanların açıkça belirtilmiş olmasa da bazı noktalara ilişkin standart varsayımlarda bulunduğunu ileri sürdü (2003:10). Bu meseleler matematiksel açıdan önemli olsa da, bu etmenleri ele alırken dahi neredeyse tüm insanlar hâlâ, açılmamış iki kapının olasılığının eşit olduğunu ve dolayısıyla kapı değiştirmenin bir şeyi değiştirmeyeceğini düşünür (Mueser and Granberg, 1999). Bu "eşit olasılık" varsayımı, derin şekilde kökleşmiş bir sezgidir (Falk 1992:202). İnsanlar öyle olsa da olmasa da, olasılıkların o anda mevcut tüm bilinmeyenler arasında eşit şekilde dağıldığını güçlü biçimde düşünme eğilimindedir (Fox and Levav, 2004:637).

Monty Hall problemi açısından kökleşmiş bir diğer nokta ise, zaten bilinmekte olan bilgilerin ortaya çıkarılmasının olasılıkları etkilemeyeceğine duyulan inançtır (Falk 1992:207). Bu yöndeki sezgi, sunucunun bir kapıyı açmasının, yarışmacının en başta 1/3 olan arabayı bulma olasılığını değiştirmeyeceğini öne süren çözümlerin de temelini oluşturur. Tam problem için bu sezgi, seçimi değiştirmenin 2/3 olasılıkla kazandıracağı doğru sonucuna götürür; ancak, doğru yanıtın bu olmadığı kısmen değiştirilmiş problemlerde de götüreceği sonuç aynıdır (Falk 1992:207).

According to Morgan et al. (1991) "The distinction between the conditional and unconditional situations here seems to confound many." That is, they, and some others, interpret the usual wording of the problem statement as asking about the conditional probability of winning given which door is opened by the host, as opposed to the overall or unconditional probability. These are mathematically different questions and can have different answers depending on how the host chooses which door to open when the player's initial choice is the car (Morgan et al., 1991; Gillman 1992). For example, if the host opens Door 3 whenever possible then the probability of winning by switching for players initially choosing Door 1 is 2/3 overall, but only 1/2 if the host opens Door 3. In its usual form the problem statement does not specify this detail of the host's behavior, nor make clear whether a conditional or an unconditional answer is required, making the answer that switching wins the car with probability 2/3 equally vague. Many commonly presented solutions address the unconditional probability, ignoring which door was chosen by the player and which door opened by the host; Morgan et al. call these "false solutions" (1991). Others, such as Behrends (2008), conclude that "One must consider the matter with care to see that both analyses are correct."

Anlamaya yardımcı olacak noktalar

Olasılık neden 1/2 değil?

Yarışmacının ilk turda arabalı kapıyı seçmesi için 3'te 1 şansı vardır. Sonra Monty Hall seçilmeyen iki kapıdan içinde keçi olduğunu bildiği birini rastgele olmayan şekilde açar. Eğer yarışmacı başlangıçta arabalı kapıyı seçmişse (başlangıçta şansı 1/3) geriye kalan kapıda bir keçi olacaktır. Eğer yarışmacı keçili kapıyı seçmişse (başlangıçtaki şansı 2/3) geri kalan kapıda bir araba olacaktır.

Buradaki kritik nokta Monty'nin bir kapıyı rastgele seçmediğidir - yarışmacı tercihini yaptığında Monty içinde keçi olduğunu bildiği bir kapıyı seçer. Bunun anlamı Monty'nin seçiminin, başlangıçta arabanın yarışmacının kapısının ardında olma olasılığını etkilemeyeceğidir. Yarışmacıya kapıyı değiştirip değiştirmeyeceği sorulduğunda, hala başlangıçta arabalı kapı seçilme olasılığı 3'te 1 ve keçili kapı seçilme olasılığı 3'te 2'dir. Ancak şimdi Monty diğer kapılardan birini açar ve açtığı kapıda araba bulunamaz, yani yarışmacının kapısında keçi bulunma olasılığı 3'te 2 ve kalan kapıda araba olma olaslığı da 3'te 2'dir.

Bu Monty'nin kapısını rastgele seçmesi ve arabayı açığa çıkarması ihtimalinin var olmasından farklı bir senaryodur. Bu durumda keçinin açığa çıkması, yarışmacının başlangıç seçimininin araba olması olasılığını 2'de 1'e yükseltecektir. Bu farklılık orijinal problemin, vos Savant'ın 2006 Kasım'ındaki köşesinde görülen değiştirilmiş versiyonu ile karşılaştırılması ile ispatlanabilir. Bu versiyonda Monty Hall hangi kapıda arabanın saklandığını unutur. Kapılardan birini rastgele seçer ve keçi açığa çıktığında rahatlar. Yarışmacıya kapısını değiştirip değiştirmeyeceği sorulduğunda vos Savant doğru bir şekilde yanıtlar "Eğer sunucu bilmiyorsa, değiştirmeniz ya da değiştirmemeniz hiçbir şey farkettirmez. Eğer sunucu biliyorsa değiştirin" (vos Savant, 2006).

Another way of looking at the situation is to consider that if the contestant chooses to switch then they are effectively getting to see what is behind 2 of the 3 doors, and will win if either one of them has the car. In this situation one of the unchosen doors will have the car 2/3 of the time and the other will have a goat 100% of the time. The fact that Monty Hall shows one of the doors has a goat before the contestant makes the switch is irrelevant, because one of the doors will always have a goat and Monty has chosen it deliberately. The contestant still gets to look behind 2 doors and win if either has the car, it is just confirmed that one of doors will have a goat first.

Kapıların sayısını artırmak

Aynı problemde kapıların sayısının üç yerine 1.000.000 olduğunu düşünmek, çözümü kavramayı kolaylaştırabilir (vos Savant 1990; Nesin 2009). Bu durumda ardında keçi olan 999.999 kapı ve ödül bulunan bir kapı olur. Yarışmacı bir kapıyı seçer. Daha sonra sunucu diğer 999.998 kapıyı açarak keçileri gösterir - sunucunun ilk kapıdan başlayarak 1.000.000 kapılık sırayı takip ettiğini, her birini açtığını, yalnızca yarışmacının seçtiği kapı ile başka bir kapıyı daha atladığını düşünelim. Ardından sunucu yarışmacıya açılmamış diğer kapıyı seçme şansı olduğunu söyler. Ortalama 1.000.000'da 999.999 olasılıkla diğer kapı ödüle açılır, zira 1.000.000'da 999.999 olasılıkla yarışmacının ilk seçtiği kapının ardında keçi vardır. Akılcı bir yarışmacı kapıyı değiştirmelidir. Sezgisel bakılırsa, yarışmacı, bir milyon kapı içinden doğru olanı seçmeyi başarma olasılığını sorgulamalıdır. Örnek, seçimi değiştirerek başarı sağlama olasılığının (1 eksi ilk seçimde doğru kapıyı seçme olasılığı) her sayıda kapı için eşit olduğunu ortaya koymak için de kullanılabilir. Ancak unutulmamalı ki, bu örnek, sunucunun ödülün nerede olduğunu bildiği varsayımına ve ödülü saklayan kapıyı açmaması gereğine dayanır. Eğer yarışmacı ilk seçiminde ödülü saklayan kapıyı bulmayı başarmışsa, sunucu açmayacağı diğer kapıyı rastgele seçer.

Bu örnek, sunucunun ödülün yerini bilmediği ve kapıları rastgele açtığı tam tersi bir durumu açıklamakta da kullanılabilir. 1.000.000'da 999.999 olasılıkla yarışmacı en başta yanlış kapıyı seçecektir, ödül diğer kapılardan birinin ardındadır. Eğer sunucu ödülün yerini bilmeksizin kapıları rastgele açıyorsa, aralarında yeni bir seçim yapılacak son iki kapıya (yarışmacının seçimi ile diğer kapı) gelmeden, büyük olasılıkla ödülü saklayan kapıyı açacaktır. Bu durum bir başka yarışma programı olan Deal or No Deal'a benzer. Bu programda yarışmacı numaralandırılmış bir çantayı seçer ve daha sonra diğerlerini her defasında bir tane olmak üzere açar.

Stibel ve diğerleri (2008) çalışan zihin talebinin Monty Hall problemi sırasında zorlandığını ve bunun, insanların seçimlerinin iki eşit olasılıklı seçeneğe dönüşerek çökmesine yol açtığını öne sürdü. Ayrıca seçeneklerin (kapıların) sayısının yedinin üzerine çıkmasının insanlardaki seçimi değiştirme eğilimini artırdığını; ancak, yine de çoğunluğun hâlâ başarı şansını hatalı olarak yarı yarıya gördüğünü ortaya koydu.

Simülasyon yoluyla çözüm

Monty Hall probleminin 30 sonucunun oyun kartlarına uyarlanması.

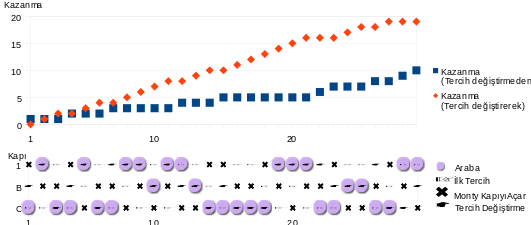
Seçimi değiştirme stratejisinin gerçekten ortalama üçte iki olasılıkla kazandıracağını ispatlamanın basit bir yolu da, yarışmayı oyun kartlarına uyarlamaktır (Gardner 1959b; vos Savant 1996:8). Alelâde bir desteden üç kart, üç kapıyı temsil eder. Maça ası gibi bir 'özel' kart arabayı saklayan kapıyı, iki kırmızı ikili gibi iki sıradan kart da, keçileri saklayan kapıları temsil eder.

Şu yöntem defalarca tekrarlanarak oyunun birçok devresi uyarlanabilir: Yarışmacının ilk seçimini temsil eden kart yarışmacının önünde ters şekilde durur. Daha sonra en az biri kırmızı ikili olan iki karta bakan sunucu, kırmızı ikili olan bir kartı açar. Eğer sunucunun elinde kalan kart Maça ası ise, bu, yarışmacının seçimini değiştirerek kazanacağı bir devredir. Eğer sunucunun elinde kalan kart kırmızı ikili ise, bu, yarışmacının ilk seçiminde ısrar ederek kazanacağı bir devredir.

Büyük sayılar yasasına göre bu deney, kazanma olasılığını yaklaşık olarak ortaya koyar ve deneyi yeterli defa tekrarlamak yalnızca yarışmacının seçimini değiştirerek üçte iki olasılıkla kazanacağını değil, bunun nedenini de gösterir. Yarışmacıya bir kart dağıtıldıktan sonra, değiştirmenin kazandırıp kazandırmayacağı zaten bellidir ve Maça ası, üçte iki olasılıkla sunucunun elindedir.

Bu ikna edici değilse, benzetme, kartlardan biri yarışmacıya verilmek ve kalan 51'i sunucuda kalmak üzere tüm bir desteyle de yapılabilir (Gardner 1959b; Adams 1990). Bu durumda Maça ası 52'de 51 olasılıkla sunucudadır ve kaç Maça ası olmayan kart açılırsa açılsın, onda kalmaya devam eder.

vos Savant'ın öne sürdüğü bir başka benzetmede, sunucu kapıları temsil eden üç kupadan birinin altında arabayı temsil eden bir madeni parayı ya da deniz kabuklarının altında bir bezelyeyi saklar.

Değişik biçimler - kısmen değiştirilmiş problemler

Diğer sunucu davranışları

The version of the Monty Hall problem published in Parade in 1990 did not specifically state that the host would always open another door, or always offer a choice to switch, or even never open the door revealing the car. However, vos Savant made it clear in her second followup column that the intended host's behavior could only be what led to the 2/3 probability she gave as her original answer. "Anything else is a different question" (vos Savant, 1991). "Virtually all of my critics understood the intended scenario. I personally read nearly three thousand letters (out of the many additional thousands that arrived) and found nearly every one insisting simply that because two options remained (or an equivalent error), the chances were even. Very few raised questions about ambiguity, and the letters actually published in the column were not among those few." (vos Savant, 1996) The answer follows if the car is placed randomly behind any door, the host must open a door revealing a goat regardless of the player's initial choice and, if two doors are available, chooses which one to open randomly (Mueser and Granberg, 1999). The table below shows a variety of OTHER possible host behaviors and the impact on the success of switching.

Determining the player's best strategy within a given set of other rules the host must follow is the type of problem studied in game theory. For example, if the host is not required to make the offer to switch the player may suspect the host is malicious and makes the offers more often if the player has initially selected the car. In general, the answer to this sort of question depends on the specific assumptions made about the host's behaviour, and might range from "ignore the host completely" to 'toss a coin and switch if it comes up heads', see the last row of the table below.

Morgan et al. (1991) and Gillman (1992) both show a more general solution where the car is randomly placed but the host is not constrained to pick randomly if the player has initially selected the car, which is how they both interpret the well known statement of the problem in Parade despite the author's disclaimers. Both changed the wording of the Parade version to emphasize that point when they restated the problem. They consider a scenario where the host chooses between revealing two goats with a preference expressed as a probability q, having a value between 0 and 1. If the host picks randomly q would be 1/2 and switching wins with probability 2/3 regardless of which door the host opens. If the player picks Door 1 and the host's preference for Door 3 is q, then in the case where the host opens Door 3 switching wins with probability 1/3 if the car is behind Door 2 and loses with probability (1/3)q if the car is behind Door 1. The conditional probability of winning by switching given the host opens Door 3 is therefore (1/3)/(1/3 + (1/3)q) which simplifies to 1/(1+q). Since q can vary between 0 and 1 this conditional probability can vary between 1/2 and 1. This means even without constraining the host to pick randomly if the player initially selects the car, the player is never worse off switching. However, it is important to note that neither source suggests the player knows what the value of q is, so the player cannot attribute a probability other than the 2/3 that vos Savant assumed was implicit.

Problem belirsizken sunucunun olası davranışları
Sunucu davranışı	Sonuç
"Monty from Hell": Sunucu sadece, yarışmacının ilk tercihi kazanan kapı olduğunda, değiştirme teklifinde bulunur.(Tierney 1991).	Değiştirme sonucunda her zaman için keçi çıkar.
"Angelic Monty": Sunucu sadece, yarışmacı yanlış kapıyı seçtiğinde değiştirme teklifinde bulunur. (Granberg 1996:185).	Değiştirme her zaman için arabayı kazandırır.
"Monty Fall" or "Ignorant Monty": Sunucu kapıların arkasında ne olduğunu bilmemektedir ve rastgele açtırdığı bir kapının arkasından araba çıkmaz. (Granberg and Brown, 1995:712) (Rosenthal, 2008).	Değiştirme yüzde elli ihtimalle arabayı kazandırır.
Sunucu kapıların ardında ne olduğunu biliyordur ve (yarışmacının seçiminden önce) ardında keçi olan rastgele bir kapı seçer. Ve yarışmacıya, sadece seçimi kendisininkinden farklı ise değiştirme teklifinde bulunur.	Değiştirme yüzde elli ihtimalle arabayı kazandırır.
Sunucu her zaman bir keçiyi açığa çıkarır ve yarışmacıya tercihini değiştirme teklifinde bulunur. Sunucu p olasılıkla en soldaki keçiyi (bu yarışmacının başlangıçdaki seçimine bağlı olabilir) ve 'q=1−p olasılıkla da en sağdaki kapıyı seçer.(Morgan et al. 1991) (Rosenthal, 2008).	Eğer sunucu en sağdaki kapıyı açarsa, değiştirme 1/(1+q) olasılıkla kazandırır.
The host acts as noted in the specific version of the problem.	Switching wins the car two-thirds of the time. (Special case of the above with p=q=½)
The host is rewarded whenever the contestant incorrectly switches or incorrectly stays.	Switching wins 1/2 the time at the Nash equilibrium.
Four-stage two-player game-theoretic (Gill, 2009a, Gill, 2009b, Gill, 2010). The player is playing against the show organisers (TV station) which includes the host. First stage: organizers choose a door (choice kept secret from player). Second stage: player makes a preliminary choice of door. Third stage: host opens a door. Fourth stage: player makes a final choice. The player wants to win the car, the TV station wants to keep it. This is a zero-sum two-person game. By von Neumann's theorem from game theory, if we allow both parties fully randomized strategies there exists a minimax solution or Nash equilibrium.	Minimax solution (Nash equilibrium): car is first hidden uniformly at random and host later chooses uniform random door to open without revealing the car and different from player's door; player first chooses uniform random door and later always switches to other closed door. With his strategy, the player has a win-chance of at least 2/3, however the TV station plays; with the TV station's strategy, the TV station will lose with probability at most 2/3, however the player plays. The fact that these two strategies match (at least 2/3, at most 2/3) proves that they form the minimax solution.
As previous, but now host has option not to open a door at all.	Minimax solution (Nash equilibrium): car is first hidden uniformly at random and host later never opens a door; player first chooses a door uniformly at random and later never switches. Player's strategy guarantees a win-chance of at least 1/3. TV station's strategy guarantees a lose-chance of at most 1/3.

N sayıda kapı

D. L. Ferguson (Selvin 1975b'deki alıntıya göre 1975'te Selvin'e yazdığı bir mektubunda) orijinal oyunun bir N sayıda kapı şeklinde genelleştirilmişini önermektedir. Bu durumda sunucu p sayıda kaybeden kapıyı açar ve oyuncuya değiştirme fırsatını verir; bu şekilde değiştirmeyle kazanma olasılığı (N−1)/[N(N−p−1)] olur. Sunucu sadece bir kapıyı açmışsa bile oyuncunun değiştirmesi yine de yararına olur ancak N sayısı büyüdükçe avantaj da sıfıra yaklaşır (Granberg 1996:188). Diğer uç durumda sunucu bir kaybeden kapı dışında diğerlerinin tamamını açarsa, değiştirmeyle kazanma şansı 1'e yaklaşır.

Bapeswara Rao ve Rao (1992) farklı bir N sayıda kapı versiyonu önermektedir. Bu versiyonda sunucu oyuncunun seçiminden faklı bir kaybeden kapı açmaktadır. Sunucu, geriye yalnızca iki kapı kalana kadar her kapı açışında oyuncuya tercihini değiştirmesi için bir fırsat verir. Dört kapı ile yapılabilecek en uygun strateji önce kapıyı seçmek ardından sadece iki kapı kalınca tercihi değiştirmek olacaktır. N sayıda kapı ile bu stratejinin kazanma olasılığı (N−1)/N'dir ve bunun en uygunu olduğu iddia edilmektedir.

Quantum version

A quantum version of the paradox illustrates some points about the relation between classical or non-quantum information and quantum information, as encoded in the states of quantum mechanical systems. The formulation is loosely based on Quantum game theory. The three doors are replaced by a quantum system allowing three alternatives; opening a door and looking behind it is translated as making a particular measurement. The rules can be stated in this language, and once again the choice for the player is to stick with the initial choice, or change to another "orthogonal" option. The latter strategy turns out to double the chances, just as in the classical case. However, if the show host has not randomized the position of the prize in a fully quantum mechanical way, the player can do even better, and can sometimes even win the prize with certainty (Flitney and Abbott 2002, D'Ariano et al. 2002).

Problemin tarihi

Monty Hall problemine benzer birkaç olasılık bulmacasından en eskisi Bertrand'ın kutu paradoksudur. Bu 1889'da Joseph Bertrand tarafından Calcul des probabilités adlı kitabında ortaya atıldı (Barbeau 1993). Bu bulmacada üç kutu bulunur: bir kutu iki altın madeni para, bir kutu iki gümüş madeni para ve bir kutu da her birinden birer tane madeni para içerir. Bir kutunun rastgele seçilmesinin ve bir madeni paranın rastgele çekilmesinin ardından, çekilen paranın altın olması durumunda geriye kalan paranın altın olma olasılığı nedir. Monty Hall probleminde olduğu gibi burada da sezgisel yanıt 1/2'dir, halbuki olasılık 2/3'tür.

Martin Gardner'ın Scientific American'daki Mathematical Games köşesinde 1959'da yayınlanan üç mahkûm problemi (1959a, 1959b), Monty Hall probleminin izomorfudur. Problem, rastgele içlerinden biri gizlice seçilip affedilecek olan üç mahkûmu içerir. Mahkûmlardan biri, diğer mahkûmlardan idam edilecek olanın adını söylemesi için gardiyana yalvarır. Bu mahkûmun kendi kaderi hakkında hiçbir bilgiyi açığa çıkarmasa da kendi affedilme şansını 1/3'ten 1/2'ye çıkarır. The warden obliges, (secretly) flipping a coin to decide which name to provide if the prisoner who is asking is the one being pardoned. The question is whether knowing the warden's answer changes the prisoner's chances of being pardoned. This problem is equivalent to the Monty Hall problem; the prisoner asking the question still has a 1/3 chance of being pardoned but his unnamed cohort has a 2/3 chance.

Steve Selvin 1975'te American Statistician dergisine gönderdiği bir çift mektup ile Monty Hall problemini ortaya attı (1975a, 1975b). İlk mektup, 15 yıl sonra Parade dergisinde yayınlanan gösterime yakın bir problem içeriyordu. İkici mektup "Monty Hall problemi" teriminin ilk kullanımı gibi görünmektedir. Problem aslında yarışma programının bir ekstrapolasyonudur. Monty Hall heyecan yaratmak için yanlış bir kapıyı açar ve yarışmacıya, kapı değiştirme fırsatı yerine 100 $ gibi daha küçük bir ödül teklif eder. Monty Hall'ün Selvin'e yazdığı bir mektuba göre:

And if you ever get on my show, the rules hold fast for you—no trading boxes after the selection. (Hall 1975)

A version of the problem very similar to the one that appeared three years later in Parade was published in 1987 in the Puzzles section of The Journal of Economic Perspectives (Nalebuff 1987).

Phillip Martin's article in a 1989 issue of Bridge Today magazine titled "The Monty Hall Trap" (Martin 1989) presented Selvin's problem as an example of what Martin calls the probability trap of treating non-random information as if it were random, and relates this to concepts in the game of bridge.

A restated version of Selvin's problem appeared in Marilyn vos Savant's Ask Marilyn question-and-answer column of Parade in September 1990 (vos Savant 1990). Though vos Savant gave the correct answer that switching would win two-thirds of the time, she estimates the magazine received 10,000 letters including close to 1,000 signed by PhDs, many on letterheads of mathematics and science departments, declaring that her solution was wrong (Tierney 1991). Due to the overwhelming response, Parade published an unprecedented four columns on the problem (vos Savant 1996:xv). As a result of the publicity the problem earned the alternative name Marilyn and the Goats.

In November 1990, an equally contentious discussion of vos Savant's article took place in Cecil Adams's column The Straight Dope (Adams 1990). Adams initially answered, incorrectly, that the chances for the two remaining doors must each be one in two. After a reader wrote in to correct the mathematics of Adams' analysis, Adams agreed that mathematically, he had been wrong, but said that the Parade version left critical constraints unstated, and without those constraints, the chances of winning by switching were not necessarily 2/3. Numerous readers, however, wrote in to claim that Adams had been "right the first time" and that the correct chances were one in two.

The Parade column and its response received considerable attention in the press, including a front page story in the New York Times (Tierney 1991) in which Monty Hall himself was interviewed. He appeared to understand the problem, giving the reporter a demonstration with car keys and explaining how actual game play on Let's Make a Deal differed from the rules of the puzzle.

Over 40 papers have been published about this problem in academic journals and the popular press (Mueser and Granberg 1999). Barbeau 2000 contains a survey of the academic literature pertaining to the Monty Hall problem and other closely related problems.

The problem continues to resurface outside of academia. The syndicated NPR program Car Talk featured it as one of their weekly "Puzzlers," and the answer they featured was quite clearly explained as the correct one (Magliozzi and Magliozzi, 1998). An account of the Hungarian mathematician Paul Erdős's first encounter of the problem can be found in The Man Who Loved Only Numbers—like many others, he initially got it wrong. The problem is discussed, from the perspective of a boy with Asperger syndrome, in The Curious Incident of the Dog in the Night-time, a 2003 novel by Mark Haddon. The problem is also addressed in a lecture by the character Charlie Eppes in an episode of the CBS drama NUMB3RS (Episode 1.13) and in Derren Brown's 2006 book Tricks Of The Mind. Penn Jillette explained the Monty Hall Problem on the "Luck" episode of Bob Dylan's Theme Time Radio Hour radio series. The Monty Hall problem appears in the film 21 (Bloch 2008). Economist M. Keith Chen identified a potential flaw in hundreds of experiments related to cognitive dissonance that use an analysis with issues similar to those involved in the Monty Hall problem (Tierney 2008).

Ayrıca bakınız

• Bayes teoremi: Monty Hall problemi
• Sınırlı seçenek prensibi (köprü)
• Make Your Mark (Pricing Game)

Benzer problemler

• Bertrand'ın kutu paradoksu (üç kart problemi olarak ta bilinir)
• Erkek mi Kız mı paradoksu
• Üç Mahkum problemi
• İki zarf problemi
• Uyuyan Güzel problemi

Kaynaklar

• Adams, Cecil (1990)."On 'Let's Make a Deal,' you pick Door #1. Monty opens Door #2—no prize. Do you stay with Door #1 or switch to #3?", The Straight Dope, (November 2, 1990). Retrieved July 25, 2005.
• Bapeswara Rao, V. V. and Rao, M. Bhaskara (1992). "A three-door game show and some of its variants". The Mathematical Scientist 17(2): 89–94.
• Barbeau, Edward (1993). "Fallacies, Flaws, and Flimflam: The problem of the Car and Goats". The College Mathematics Journal 24(2): 149-154.
• Barbeau, Edward (2000). Mathematical Fallacies, Flaws and Flimflam. The Mathematical Association of America. ISBN 0-88385-529-1.
• Behrends, Ehrhard (2008). Five-Minute Mathematics. AMS Bookstore. s. 57. ISBN 978-0-8218-4348-2. http://books.google.com/books?id=EpkyE6JFmkwC&pg=PA48&dq=monty-hall+door-number&lr=&as_brr=0&as_pt=ALLTYPES&ei=fI3iSeqLLo_ElQTmzq2fDQ#PPA57,M1. 
• Bloch, Andy (2008). "21 - The Movie (my review)". 28 Temmuz 2011 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20110728063055/http://www.andybloch.com/gl/pub/article.php?story=2008031308241327. Erişim tarihi: 2008-05-05. 
• Chun, Young H. (1991). "Game Show Problem," OR/MS Today 18(3): 9.
• D'Ariano, G.M et al. (2002). "The Quantum Monty Hall Problem" (PDF). Los Alamos National Laboratory, (February 21, 2002). Retrieved January 15, 2007.
• Devlin, Keith (July – August 2003). "Devlin's Angle: Monty Hall". The Mathematical Association of America. 2 Temmuz 2013 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20130702043408/http://www.maa.org/devlin/devlin_07_03.html. Erişim tarihi: 2008-04-25. 
• "The Monty Hall puzzle". The Economist (The Economist Newspaper) 350: s. 110. 1999. http://books.google.com/books?id=H3vPAAAAIAAJ&q=goat-b+goat-a&dq=goat-b+goat-a&lr=&as_brr=0&as_pt=ALLTYPES&ei=yTLhSbvzJYuIkASxlsinDQ&pgis=1. 
• Falk, Ruma (1992). "A closer look at the probabilities of the notorious three prisoners," Cognition 43: 197–223.
• Flitney, Adrian P. and Abbott, Derek (2002). "Quantum version of the Monty Hall problem," Physical Review A, 65, Art. No. 062318, 2002.
• Fox, Craig R. and Levav, Jonathan (2004). "Partition-Edit-Count: Naive Extensional Reasoning in Judgment of Conditional Probability," Journal of Experimental Psychology: General 133(4): 626-642.
• Gardner, Martin (1959a). "Mathematical Games" column, Scientific American, October 1959, pp. 180–182. Reprinted in The Second Scientific American Book of Mathematical Puzzles and Diversions.
• Gardner, Martin (1959b). "Mathematical Games" column, Scientific American, November 1959, p. 188.
• Gill, Jeff (2002). Bayesian Methods, pp. 8–10. CRC Press. ISBN 1-58488-288-3, (Google Kitaplar'da restricted online copy)
• Gill, Richard (2009a) Probabilistic and Game Theoretic Solutions to the Three Doors Problem, prepublication, http://www.math.leidenuniv.nl/~gill/threedoors.pdf.
• Gill, Richard (2009b) Supplement to Gill (2009a), prepublication, http://www.math.leidenuniv.nl/~gill/quizmaster2.pdf
• Gill, Richard (2010) Second supplement to Gill (2009a), prepublication, http://www.math.leidenuniv.nl/~gill/montyhall3.pdf
• Gillman, Leonard (1992). "The Car and the Goats," American Mathematical Monthly 99: 3–7.
• Granberg, Donald (1996). "To Switch or Not to Switch". Appendix to vos Savant, Marilyn, The Power of Logical Thinking. St. Martin's Press. ISBN 0-612-30463-3, (Google Kitaplar'da restricted online copy).
• Granberg, Donald and Brown, Thad A. (1995). "The Monty Hall Dilemma," Personality and Social Psychology Bulletin 21(7): 711-729.
• Grinstead, Charles M. and Snell, J. Laurie (04.07.2006) (PDF). Grinstead and Snell’s Introduction to Probability. http://www.math.dartmouth.edu/~prob/prob/prob.pdf. Erişim tarihi: 02.04.2008.  Online version of Introduction to Probability, 2nd edition, published by the American Mathematical Society, Copyright (C) 2003 Charles M. Grinstead and J. Laurie Snell.
• Hall, Monty (1975). The Monty Hall Problem. LetsMakeADeal.com. Includes May 12, 1975 letter to Steve Selvin. Retrieved January 15, 2007.
• Henze, Norbert (1997). Stochastik für Einsteiger: Eine Einführung in die faszinierende Welt des Zufalls‎, pp. 105, Vieweg Verlag, ISBN 3-8348-0091-0, (Google Kitaplar'da restricted online copy)
• Herbranson, W. T. and Schroeder, J. (2010). "Are birds smarter than mathematicians? Pigeons (Columba livia) perform optimally on a version of the Monty Hall Dilemma." J. Comp. Psychol. 124(1): 1-13. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/20175592 March 1, 2010.
• Krauss, Stefan and Wang, X. T. (2003). "The Psychology of the Monty Hall Problem: Discovering Psychological Mechanisms for Solving a Tenacious Brain Teaser," Journal of Experimental Psychology: General 132(1). Retrieved from http://www.usd.edu/~xtwang/Papers/MontyHallPaper.pdf March 30, 2008.
• Mack, Donald R. (1992). The Unofficial IEEE Brainbuster Gamebook. Wiley-IEEE. s. 76. ISBN 978-0-7803-0423-9. http://books.google.com/books?id=hcy9mQp83dEC&pg=PA18&dq=%22monty+hall+problem%22&lr=&as_drrb_is=b&as_minm_is=0&as_miny_is=&as_maxm_is=0&as_maxy_is=1995&as_brr=3&as_pt=ALLTYPES&ei=MqDVSYDkHpeSkASZvbi-Bg#PPA76,M1. 
• Magliozzi, Tom; Magliozzi, Ray (1998). Haircut in Horse Town: & Other Great Car Talk Puzzlers. Diane Pub Co.. ISBN 0-7567-6423-8. 
• Martin, Phillip (1989). "The Monty Hall Trap", Bridge Today, May–June 1989. Reprinted in Granovetter, Pamela and Matthew, ed. (1993), For Experts Only, Granovetter Books.
• Martin, Robert M. (2002). There are two errors in the the title of this book (2nd bas.). Broadview Press. s. 57–59. ISBN 978-1-55111-493-4. http://books.google.com/books?id=d6w6Wyp5cyUC&pg=PA57&dq=monty-hall+door-number&lr=&as_brr=0&as_pt=ALLTYPES&ei=fI3iSeqLLo_ElQTmzq2fDQ#PPA59,M1. 
• Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). "Let's make a deal: The player's dilemma," American Statistician 45: 284-287.
• Mueser, Peter R. and Granberg, Donald (May 1999). "The Monty Hall Dilemma Revisited: Understanding the Interaction of Problem Definition and Decision Making", University of Missouri Working Paper 99-06. Retrieved July 5, 2005.
• Nalebuff, Barry (1987). "Puzzles: Choose a Curtain, Duel-ity, Two Point Conversions, and More," Journal of Economic Perspectives 1(2): 157-163 (Autumn, 1987).
• Nesin, Ali (2009). Matematik ve Oyun (2. bas.). Nesin Yayıncılık. s. 1-5. ISBN 978-975-9038-89-2. 
• Rosenthal, Jeffrey S. (September 2008). "Monty Hall, Monty Fall, Monty Crawl". Math Horizons: 5–7. http://probability.ca/jeff/writing/montyfall.pdf. 
• Selvin, Steve (1975a). "A problem in probability" (letter to the editor). American Statistician 29(1): 67 (February 1975).
• Selvin, Steve (1975b). "On the Monty Hall problem" (letter to the editor). American Statistician 29(3): 134 (August 1975).
• Seymann R. G. (1991). "Comment on Let's make a deal: The player's dilemma," American Statistician 45: 287-288.
• Stibel, Jeffrey, Dror, Itiel, & Ben-Zeev, Talia (2008). "The Collapsing Choice Theory: Dissociating Choice and Judgment in Decision Making," Theory and Decision. Full paper can be found at http://users.ecs.soton.ac.uk/id/TD%20choice%20and%20judgment.pdf.
• Tierney, John (1991). "Behind Monty Hall's Doors: Puzzle, Debate and Answer?", The New York Times, 1991-07-21. Retrieved on 2008-01-18.
• Tierney, John (2008). "And Behind Door No. 1, a Fatal Flaw", The New York Times, 2008-04-08. Retrieved on 2008-04-08.
• vos Savant, Marilyn (1990). "Ask Marilyn" column, Parade Magazine p. 16 (9 September 1990).
• vos Savant, Marilyn (1991). "Ask Marilyn" column, Parade Magazine p. 12 (17 February 1991).
• vos Savant, Marilyn (1996). The Power of Logical Thinking. St. Martin's Press. ISBN 0-312-15627-8. http://books.google.com/books?id=pgQQv8W_IgIC&pg=PA5&dq=%22monty+hall+paradox%22+inauthor:savant&lr=&as_brr=0&as_pt=ALLTYPES&ei=aETYSZDDDoWqlQSIgMHlAg#PPA6,M1. 
• vos Savant, Marilyn (2006). "Ask Marilyn" column, Parade Magazine p. 6 (26 November 2006).
• Schwager, Jack D. (1994). The New Market Wizards. Harper Collins. s. 397. ISBN 978-0-88730-667-9. http://books.google.com/books?id=Ezz_gZ-bRzwC&pg=PA397&dq=three-doors+monty-hall&lr=&as_drrb_is=b&as_minm_is=0&as_miny_is=&as_maxm_is=12&as_maxy_is=1994&as_brr=3&as_pt=ALLTYPES&ei=qRTYSZOjLIzOkATFw_HwAg. 
• Williams, Richard (2004). "Appendix D: The Monty Hall Controversy" (PDF). Course notes for Sociology Graduate Statistics I. 13 Mart 2016 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20160313052134/http://www3.nd.edu/~rwilliam/stats1/appendices/xappxd.pdf. Erişim tarihi: 2008-04-25. 
• Wheeler, Ward C. (1991). "Congruence Among Data Sets: A Bayesian Approach". Michael M. Miyamoto and Joel Cracraft. Phylogenetic analysis of DNA sequences. Oxford University Press US. s. 335. ISBN 978-0-19-506698-2. http://books.google.com/books?id=1wqvNgz58JQC&pg=PA335&dq=%22monty+hall%22+unchanged+switch&lr=&as_brr=3&as_pt=ALLTYPES&ei=FsnSSYeXFo7skwT64ezkCQ. 
• Whitaker, Craig F. (1990). [Letter]. "Ask Marilyn" column, Parade Magazine p. 16 (9 September 1990).

Dış bağlantılar

Vikikitapta bu konu hakkında daha fazla bilgi var:

Algorithm Implementation

• The Game Show Problem–the original question and responses on Marilyn vos Savant's web site
• Açık Dizin Projesi'nde Monty Hall kategorisi
• "Monty Hall Paradox" by Matthew R. McDougal, The Wolfram Demonstrations Project (simulation)
• The Monty Hall Problem at The New York Times (simulation)