Petri ağı

Bir Petri ağı (yer/geçiş ağı, yerleşim/geçiş ağı veya Y/G ağı olarak da bilinir) sistemlerin incelenmesi için kullanılabilecek bir araçtır. Petri ağları, sistemin matematiksel bir modelle modellenebilmesine izin verir. Bir Petri ağı, geçiş ve yerleşim düğümlerinden oluşan tek yönlü iki parçalı graf olarak da tanımlanabilir. Ok şeklinde gösterilen yönlü eğriler, bir geçişten önce ve sonra hangi yerlerin olduğunu tanımlarlar.

Bazı kaynaklar Petri ağlarının 1939 Ağustos'unda, henüz 13 yaşında olan Carl Adam Petri tarafından, kimyasal prosesleri tarif etmek amacıyla bulunduğunu belirtirler.

Petri ağları, UML, BPMN ve EPC gibi endüstri standartlarına benzer şekilde seçim, tekrarlama, eşzamanlı çalışma gerektiren adımlı prosesler için bir grafiksel notasyon sunar. Ancak bu standartların ötesinde, proses analizi için geliştirilmiş matematiksel teorisiyle ilgili proseslerin çalışmasını matematiksel bir kesinlikte modelleyebilir.

(a) Petri ağ yörüngesi örneği

Petri ağ temelleri

Bir petri ağı yerler, geçişler ve eğrilerden oluşur. Yerler ve geçişler, graf teorisindeki düğümler ve kenarlar ile eşdeğerdir. Eğriler bir yerden bir geçişe veya bir geçişten bir yere doğru koşarlar. İki yer arasında veya iki geçiş arasında bir eğri olamaz. Geçişe giriş yapan eğri hangi yerden çıkış yaptıysa, bu yere geçişin giriş yeri; Geçişten çıkış yapan eğri hangi yere giriş yaptıysa, bu yere geçişin çıkış yeri denir.

Grafiksel olarak bir Petri ağındaki bir yer ayrık sayıdaki işaretler içerebilir. Bu işaretler jeton olarak adlandırılır. Jetonların herhangi bir anda yerler üzerindeki dağılımı işaretleme, jeton dağılımı veya konfigürasyon olarak adlandırılır.

Bir geçişin giriş yerlerinde yeterli jeton var ise, bu geçiş etkinleştirilmiş veya tetiklenebilir denir.

Etkinleştirilmiş bir diğer ifade ile, tetiklenebilir bir geçiş tetiklendiğinde, giriş yerlerinden ihtiyaç duyulan miktarda jeton tüketir ve çıkış yerlerinde üretilmesi gereken miktarda jeton üretilir. Bu 'gereken' miktarlar, ilgili geçişin ağırlığı, ayrık sistemler için özelleştirirsek geçişin üzerinde yazan rakam, ile gösterilir.

Tetikleme atomiktir. Yani anlık olarak, tek bir seferde gerçekleşir ve yarıda bırakılamaz.

Bir çalışma kuralı tanımlanmadığı sürece, Petri ağlarının çalışması nondeterministictir: Aynı anda birden fazla geçiş tetiklendiğinde, hangisinin tetikleneceği bilinemez ya da bir başka deyişle, geçişlerin herhangi birisi tetiklenebilir.

Tetikleme deterministik olmadığından ve ağda herhangi bir yerde birden fazla sayıda jeton bulunabileceğinden, Petri ağları dağıtılmış sistemlerin eşzamanlı davranışını modellemek için uygundur.

Resmi tanım ve temel terminoloji

Petri ağları basit ağ olarak adlandırılan ağların kapsamını genişleten durum-geçiş sistemleridir.^[1]

Tanım 1. Bir ${\displaystyle N=(P,T,F)}$ ağı üç parametrelidir, öyle ki:

1. ${\displaystyle P}$ ve ${\displaystyle T}$ sırasıyla yerlerin ve geçişlerin ayrık sonlu kümeleridir.
2. ${\displaystyle F\subset (P\times T)\cup (T\times P)}$ ya da akış ilişkilerinin(graflardaki eğrilerin) bir kümesidir.

Tanım 2. Verilen bir N = (P, T, F ) ağındaki bir konfigürasyon C kümesiyle gösterilir, öyle ki  C ⊆ P.

Aktifleştirilmiş bir geçişe sahip bir Petri ağı

Geçiş tetiklendikten Petri ağının durumu. (geçiş tetiklenmeden önceki hali yukarıda)

Tanım 3. Bir basit ağ EN = (N, C ) formundaki ağdır, öyle ki:

1. N = (P, T, F ) bir ağdır.
2. C, C ⊆ P olan bir konfigürasyondur.

Tanım 4. Bir Petri ağı, PN = (N, M, W ) formundaki ağdır ve basit ağın kapsamını genişletir, öyle ki:

1. N = (P, T, F ) bir ağdır.
2. M : P → Z Z'nin sayılabilir küme olduğu bir yerler multisetidir. M(not:marking), konfigürasyon konseptini genişletir ve Petri ağlarında genellikle işaretleme(jeton dağılımı) olarak tanımlanır.
3. W : F → Z bir eğri multisetidir. Öyle ki, W(not: weight) her eğrinin üzerindeki sayı(yahut eğrinin ağırlığı) eğri 'multiplicity'sinin(multiset içerisinde kaç defa görüldüğünün) bir ölçüsüdür.

Eğer bir Petri ağı, basit ağa eş ise, Z {0,1} sayılabilir kümesi olabilir ve P 'deki M'nin altındaki 1'e karşılık gelen elemanlar, bir konfigürasyon oluşturur. (not: özetle her yerde en fazla 1 jeton bulunur). Benzer olarak, eğer bir Petri ağı, bir basit ağ değilse, M multiseti konfigürasyonların non-singleton bir kümesi olarak ifade edilebilir. Bu bağlamda, M, basit ağlardaki konfigürasyon konseptini Petri ağlarına genişletir. (not: özetle basit bir ağda her yer sadece tek bir jeton içerebilirken, Petri ağında böyle bir kısıtlama bulunmamaktadır.)

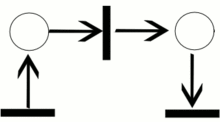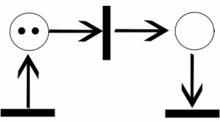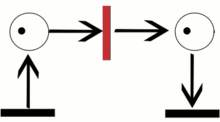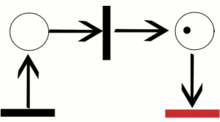
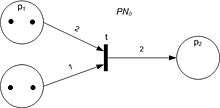
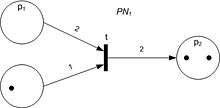
Bir Petri ağı diyagramında (sağ üst köşeye bakın), yerler genellikle çemberler tarafından, geçişler genellikle uzunca ve dar dikdörtgenler tarafından ve eğriler yerlerden geçişlere yahut geçişlerden yerlere bağlantıları gösteren tek yönlü oklar tarafından modellenir. Eğer diyagram basit bir ağa ait olsaydı, yerler yine çemberler tarafından gösterilecekti. Ancak bu defa, her bir çember bir jeton içerebilecekti. Yukarıda sağda gözüken Petri ağında, bir konfigürasyonda bir yerin kaç defa gözüktüğünün ifadesi olarak yer birden fazla jeton içermektedir. Tüm Petri ağına dağıtılmış jeton konfigürasyonuna, işaretleme adı verilir.

Yukarıda sağdaki resimde, p₁ yeri, t geçişinin giriş yeridir; p₂ yeri ise aynı geçişin çıkış yeridir. Üst resimde bulunan PN₀ Petri ağı, M₀ işaretlemesi ile alt resimde bulunan PN₁ ağı ise M₁ işaretlemesi ile konfigüre edilmiş(yahut işaretlenmiş) olsun. PN₀'ın konfigürasyonu, tüm giriş yerleri yeteri kadar sayıda jeton içerdiği (resimlerde noktalar olarak gösteriliyor) içerdiği için t geçişini etkinleştirir. bir yerin "yeteri kadar jeton" içermesi demek, o yerden geçişe giden eğrinin ağırlığına eşit veya daha fazla sayıda jetona sahip olması demektir. Bir geçiş, sadece ve sadece etkinleştirilmiş ise, tetiklenebilir. Bu örnekte, t 'nin tetiklenmesi(ateşlenmesi) M_0' konfigürasyonundan M₁ konfigürasyonuna bir geçiş yapılmasını sağlar ve PN₁ Petri ağına ulaşılması ile sonuçlanır (sağ üstte, alttaki resim).

Hatırlatma 1. "büyük veya eşittir" tabirinin kesin anlamı, tetikleme kuralındaki toplama işleminin cebirsel kesinliğine bağlıdır. Cebirsel özelliklerdeki farklı varyasyonlar bizi farklı Petri ağı sınıflarına götürebilir. Örneğin: Cebirsel Petri Ağları.

Sıradaki resmi tanım, (Peterson 1981)'in tanımıdır. Birçok alternatif tanım da mevcuttur.

Sentaks

Bir Petri ağı grafı(bazıları tarafından Petri ağı olarak da söylenir ancak aşağıya bakın) ${\displaystyle (S,T,W)\!}$ olarak ifade edilecek şekilde, üç elemanlıdır(tuple). Öyle ki:

• S yerlerin sonlu kümesidir.
• T geçişlerin sonlı kümesidir.
• S ve T ayrıktır. herhangi bir nesne, hem bir geçişte hem de bir yer olamaz.(bir nesne ya geçiştir ya yerdir).
• ${\displaystyle W:(S\times T)\cup (T\times S)\to \mathbb {N} }$ eğriler multisetidir.. Her bir eğriye, negatif olmayan bir tamsayı(Eğri ağırlığı) ataması yapar.

Akış ilişkisi eğrilerin bir kümesidir: ${\displaystyle F=\{(x,y)\mid W(x,y)>0\}}$. Birçok kitap, eğrilerin ağırlığının yalnızca 1 olabileceğini yazar. Bu yazılar genellikle Petri ağlarını W yerine F' ile tanımlarlar. Bu yaklaşım kullanıldığında, bir Petri ağı bipartite multigraph ${\displaystyle (S\cup T,F)}$ haline dönüşür.

Bir geçişin girdi kümesi(preset) t, o geçişe ait giriş yerlerinin kümesidir: ${\displaystyle {}^{\bullet }t=\{s\in S\mid W(s,t)>0\}}$; Geçişin çıktı kümesi(postset) geçişe ait çıkış yerlerinin kümesidir: ${\displaystyle t^{\bullet }=\{s\in S\mid W(t,s)>0\}}$. yerlerin girdi çıktı kümelerinin tanımları benzerdir (analoji).

Bir Petri ağının(grafının) işaretlemesi onun yerlerinin bir multisetidir.Yeni, ${\displaystyle M:S\to \mathbb {N} }$. adreslemesi için, işaretleme her yere belirli sayılarda jeton ataması yapar deriz. .

A Petri ağı (bazıları tarafından işaretli Petri ağı olarak da adlandırılır - yukarıya bakın) 4 elemanlı bir kümedir. ${\displaystyle (S,T,W,M_{0})\!}$, Öyle ki:

• ${\displaystyle (S,T,W)}$ bir petri ağıdır.
• ${\displaystyle M_{0}}$ (Petri ağına ait bir işaretleme olan) ilk işaretlemedir.

Çalışma mantığı

Kelimelerle ifade edersek:

• M işaretlemesindeki(konfigürasyonundaki) t geçişinin ateşlenmesi, geçişin giriş yerlerinden(s) ${\displaystyle W(s,t)}$ adet jetonun tüketilmesine, ve geçişin çıkış yerlerinde(s) ${\displaystyle W(t,s)}$ adet jetonun üretilmesine sebep olur.
• M işaretlemesindeki(konfigürasyonundaki) bir geçiş için, sadece ve sadece ${\displaystyle \forall s:M(s)\geq W(s,t)}$ koşulu sağlanıyorsa, yani geçişin giriş yerlerinde tüketim için yeterli jeton varsa geçiş etkinleştirilmiştir (tetiklenebilir/ateşlenebilir).

Bizler, genellikle tetiklerin rastgele zamanlarda tetiklendiği durumlarda neler olabileceği ile ilgileniriz.

Bir adımda ulaşılabilirlik

Eğer ${\displaystyle M\to _{G}M'}$ ise, M işaretlemesinden bir adımda ${\displaystyle M'}$ işaretlemesine ulaşılabilir deriz. (Ya da ${\displaystyle M'}$ , M'den bir adımda ulaşılabilirdir)

Ulaşılabilirlik

${\displaystyle {\to _{G}}^{*}}$ 'nin ${\displaystyle \to _{G}}$'nin reflexive transitive closure'u olduğu durumlarda ; ${\displaystyle M{\to _{G}}^{*}M'}$ ise, herhangi bir adım sayısında ulaşılabiliyorsa, ${\displaystyle M'}$ , M 'den ulaşılabilirdir deriz.

${\displaystyle N=(S,T,W,M_{0})\!}$, işaretli bir Petri ağı olmak üzere, ${\displaystyle M_{0}}$ ilk işaretlemesinden itibaren gerçekleştirilebilecek ateşemelerle(tetiklemelerle) ilgileniriz. Bu, ulaşılabiir işaretlemeler kümesidir ve ${\displaystyle R(N)\ {\stackrel {D}{=}}\ \{M'\mid M_{0}{\to _{(S,T,W)}}^{*}M'\}}$şeklinde gösterilir.

Ulaşılabilirlik grafı

N'nin ulaşılabilirlik grafı , onun ulaşılabilir işaretlemeleri${\displaystyle R(N)}$ ile sınırlanmış geçiş ilişkileridir ${\displaystyle \to _{G}}$ . Bu, ağın durum uzayıdır. (özetle, ağın alabileceği tüm durumları gösteren kümedir)

G grafına ve' ${\displaystyle M_{0}}$ 'ilk durumuna sahip bir Petri ağındaki ateşleme sekansı (ya da sıralı ateşleme kümesi)' ${\displaystyle {\vec {\sigma }}=\langle t_{i_{1}}\ldots t_{i_{n}}\rangle }$ 'ile gösterilir. Öyle ki;'${\displaystyle M_{0}\to _{G,t_{i_{1}}}M_{1}\wedge \ldots \wedge M_{n-1}\to _{G,t_{i_{n}}}M_{n}}$. Burada ateşleme sekanslarının kümesi ${\displaystyle L(N)}$ ile gösterilmiştir.

Tanımlardaki farklılıklar

Daha önce de belirtildiği gibi, tanım farklılıklarının an genel olanı, eğri ağırlıklarını göz ardı etmek ve W ile gösterilen eğriler mutisetini, ${\displaystyle F\subseteq (S\times T)\cup (T\times S)}$ ile gösterilen ve akış ilişkisi olarak adlandırılan bir basit küme ile değiştirmektir. Bu ifade gücünü (expressive power) sınırlandırmaz, her ikisi de birbirleri yerine kullanılabilir.

Genel olarak kullanılan bir diğer farklılık da, Desel ve Juhás (2001)'ın da kullandığı üzere,^[2] kapasitelerin yerler üzerinde tanımlanmış olmasına izin verilmesidir. Aşağıda ekler bölümünde bu konu tartışılmıştır.

Vektör ve matris şeklinde formülasyon - vektörizasyon

Bir Petri ağına ilişkin işaretlemeler(jeton dağılımları) ${\displaystyle (S,T,W,M_{0})\!}$, negatif olmayan tamsayıların ${\displaystyle |S|}$ boyutlu vektörleri olarak ifade edilebilir.

Vektörün geçiş ilişkisi, ${\displaystyle |S|}$ * ${\displaystyle |T|}$ boyutundaki bir çift matrisle gösterilebilir:

• ${\displaystyle W^{-}}$, öyle ki ${\displaystyle \forall s,t:W^{-}[s,t]=W(s,t)}$
• ${\displaystyle W^{+}}$, öyle ki ${\displaystyle \forall s,t:W^{+}[s,t]=W(t,s).}$

Ardından farkları olan

• ${\displaystyle W^{T}=W^{+}-W^{-}}$

ifadesi, ulaşılabilir jeton dağılımlarını matris çarpımı şeklinde göstermek için aşağıdaki şekilde kullanılabilir.

Herhangi bir w ateşleme(geçiş/tetikleme) sekansı için, her geçişe kendi ağırlığını w atayan bir ${\displaystyle o(w)}$ yazalım. Bu durumda

• ${\displaystyle R(N)=\{M\mid \exists w:M=M_{0}+W^{T}\cdot o(w)\wedge w\!}$, $N$'ye ait bir ateşleme sekansı'dır.${\displaystyle \}\!}$.

w'nin bir ateşleme sekansı olması gerektiğine dikkat edin; geçişlerin rastgele tetiklenmesine izin vermek, genellikle daha büyük bir küme oluşturur.

${\displaystyle W^{+}={\begin{bmatrix}*&t1&t2\\p1&0&1\\p2&1&0\\p3&1&0\\p4&0&1\end{bmatrix}}}$

${\displaystyle W^{-}={\begin{bmatrix}*&t1&t2\\p1&1&0\\p2&0&1\\p3&0&1\\p4&0&0\end{bmatrix}}}$

${\displaystyle W^{T}={\begin{bmatrix}*&t1&t2\\p1&-1&1\\p2&1&-1\\p3&1&-1\\p4&0&1\end{bmatrix}}}$

${\displaystyle M_{0}={\begin{bmatrix}1&0&2&1\end{bmatrix}}}$

Kaynakça

1. Rozenburg, G.; Engelfriet, J. (1998). "Elementary Net Systems". Reisig, W.; Rozenberg, G.. Lectures on Petri Nets I: Basic Models - Advances in Petri Nets. Lecture Notes in Computer Science. 1491. Springer. s. 12–121. 
2. Desel, Jörg; Juhás, Gabriel (2001). "What Is a Petri Net? Informal Answers for the Informed Reader". Ehrig, Hartmut; et al.. Unifying Petri Nets. LNCS. 2128. Springerlink.com. s. 1–25. http://www.springerlink.com/content/a6lmwqye66ll5w56/. Erişim tarihi: 2014-05-14.