İki parçalı graf

İki parçalı graf örneği

m=5 ve n=3 elemanlı parça kümelerinden oluşan tam iki parçalı graf örneği

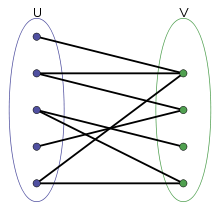
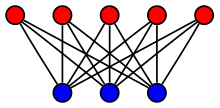
Graf teorisinde, düğümleri her kenar iki kümede de bir bitiş ucuna sahip olabilecek şekilde iki ayrı kümeye ayrılabilen graflara İki parçalı graf adı verilir.

Daha matematiksel bir ifade ile;

Düğümleri U ve V şeklinde iki ayrık ve birbirinden bağımsız kümeye ayrılabilen ve her bir kenarı U kümesindeki bir düğümü V kümesindeki bir düğüme bağlayan graflara iki parçalı graf adı verilir. Burada U ve V kümeleri, genellikle parça kümeleri (partite sets) olarak ifade edilir.

Bir başka tanımla: Tek sayıda kapalı bölge (cycle) içermeyen içermeyen herhangi bir graf, iki parçalı bir graf olarak adlandırılır.^[1][2]

${\displaystyle U}$ ve ${\displaystyle V}$ kümeleri, bir grafın renklendirilmesi olarak da düşünülebilir. Bu durumda, U kümesinin tüm elemanlarını maviye, V kümesinin tüm elemanlarını yeşile boyadığımızı düşünürsek, bu graftaki her bir kenarın(yayın, bağıntının) iki ucundaki düğümlerin farklı renklerde olacağını söyleyebiliriz^[3][4] (graf renklendirme problemi). 

Bunun tersi de geçerlidir. iki parçalı olmayan bir grafta, böyle bir renklendirme mümkün değildir. Üçgen şeklinde bir graf düşünürsek, muhakkak üç kenardan birisinin iki ucundaki düğümler aynı renkte olacaktır. 

İki parçalı grafları göstermek için genellikle ${\displaystyle G=(U,V,E)}$ notasyonu kullanılır. U ve V düğümlerin oluşturduğu parça kümelerini gösterirken, ${\displaystyle E}$ grafta yer alan kenarlar kümesini gösterir. Eğer iki parçalı graf bağlı(connected) değilse, birden fazla iki parçaya sahip olabilir ^[5]; Bu durumda ${\displaystyle (U,V,E)}$ notasyonu, bir uygulamada önemli olabilecek belirli bir 'iki parçayı' göstermekte faydalı olabilir. Eğer ${\displaystyle |U|=|V|}$ ise, yani U ve V kümeleri eşit sayıda elemana sahip iseler,  ${\displaystyle G}$ grafı, dengeli iki parçalı graf olarak adlandırılabilir.^[3] Eğer iki parçanın tek tarafından ki tüm düğümlerin derecesi aynı ise, G grafı (biregular) olarak adlandırılır.

Özellikler

Tanımlama

İki parçalı graflar birden fazla şekilde tanımlanabilir

• Bir graf ancak ve ancak, tek sayıda kapalı alan içermiyorsa, iki parçalıdır.^[6]
• Bir graf ancak ve ancak kromatik sayısı iki ve ikiden az ise, iki parçalıdır. ^[3]
• Bir grafın spektrumu ancak ve ancak graf iki parçalı ise simetriktir.^[7]

Kaynakça

1. Diestel, Reinard (2005). Graph Theory, Grad. Texts in Math. Springer. ISBN 978-3-642-14278-9. http://diestel-graph-theory.com/. 
2. Asratian, Armen S.; Denley, Tristan M. J.; Häggkvist, Roland (1998), Bipartite Graphs and their Applications, Cambridge Tracts in Mathematics, 131, Cambridge University Press, ISBN 9780521593458 .
3. Asratian, Denley & Häggkvist (1998), p. 7.
4. Scheinerman, Edward R. (2012), Mathematics: A Discrete Introduction (3rd bas.), Cengage Learning, ss. 363, ISBN 9780840049421, http://books.google.com/books?id=DZBHGD2sEYwC&pg=PA363 
5. Chartrand, Gary; Zhang, Ping (2008), Chromatic Graph Theory, Discrete Mathematics And Its Applications, 53, CRC Press, ss. 223, ISBN 9781584888000, http://books.google.com/books?id=_l4CJq46MXwC&pg=PA223 .
6. Asratian, Denley & Häggkvist (1998), Theorem 2.1.3, p. 8.
7. Biggs, Norman (1994), Algebraic Graph Theory, Cambridge Mathematical Library (2nd bas.), Cambridge University Press, ss. 53, ISBN 9780521458979, http://books.google.com/books?id=6TasRmIFOxQC&pg=PA53