Q-fonksiyonu

A plot of the Q-function.

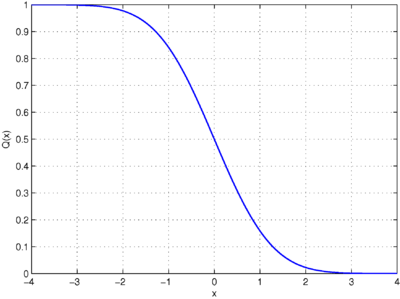
İstatistik bilimi içinde Q-fonksiyonu standart normal dağılım'ın kuyruk olasılığı'dır..^[1][2] [1] [2] Diğer bir deyişle, ${\displaystyle Q(x)}$ normal (Gauss) rastgele değişken ortalamanın üzerinde ${\displaystyle x}$'ınstandart sapmasından daha büyük bir değer elde edeceği olasılığıdır.Q-fonksiyonu diğer tanımları, bunların tümü, normal yığılımlı dağılım fonksiyonu'nun basit bir dönüştürmesi olarak zaman zaman kullanılır.^[3] Çünkü normal dağılım'ın yığılımlı dağılım fonksiyonu ile ilişkilidir ve uygulamalı matematik ve fizikte çok önemli bir işlevi olan Q-fonksiyonu hata fonksiyonu hesabı terimleri içinde ifade edilebilir.

Tanımı ve temel özellikleri

biçimsel olarak Q-fonksiyonunun tanımı

${\displaystyle Q(x)={\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }\exp {\Bigl (}-{\frac {u^{2}}{2}}{\Bigr )}\,du.}$

Böylece

${\displaystyle Q(x)=1-Q(-x)=1-\Phi (x)\,\!,}$,

burada ${\displaystyle \Phi (x)}$ Normal Gauss dağılımının yığılımlı dağılım fonksiyonu'dur Q-fonksiyonu hata fonksiyonu veya tamamlayıcı hata fonksiyonu olarak terimleri içinde ^[2] ile ifade edilebilir.

${\displaystyle Q(x)={\tfrac {1}{2}}-{\tfrac {1}{2}}\operatorname {erf} {\Bigl (}{\frac {x}{\sqrt {2}}}{\Bigr )}={\tfrac {1}{2}}\operatorname {erfc} ({\frac {x}{\sqrt {2}}}).}$

Bu ifade ${\displaystyle x}$ 'ın sadece pozitif değerler için geçerlidir ama negatif değerler için ${\displaystyle Q(x)=1-Q(-x)\,\!,}$ ile birlikte kullanılabilirler tegrasyon aralığı sonlu olduğu bu form avantajlıdır.

Sınırlar

• Q-fonksiyonu bir temel fonksiyon değildir.bununla birlikte, sınırlar

${\displaystyle {\frac {x}{1+x^{2}}}\cdot {\frac {1}{\sqrt {2\pi }}}e^{-x^{2}/2}<Q(x)<{\frac {1}{x}}\cdot {\frac {1}{\sqrt {2\pi }}}e^{-x^{2}/2},\qquad x>0,}$

büyük "x" için giderek daha sıkı olmaya ve çoğu zaman kullanışlıdır yerine koyma ${\displaystyle v=u^{2}/2}$ ve tanımı ${\displaystyle \varphi (x)={\tfrac {1}{\sqrt {2\pi }}}e^{-x^{2}/2},}$ üst sınır aşağıdaki gibi elde edilmiştir

${\displaystyle {\begin{aligned}Q(x)&=\int _{x}^{\infty }\varphi (u)\,du\\&<\int _{x}^{\infty }{\frac {u}{x}}\varphi (u)\,du=\int _{x^{2}/2}^{\infty }{\frac {e^{-v}}{x{\sqrt {2\pi }}}}\,dv=-{\biggl .}{\frac {e^{-v}}{x{\sqrt {2\pi }}}}{\biggr |}_{x^{2}/2}^{\infty }={\frac {\varphi (x)}{x}}.\end{aligned}}}$

Aynı şekilde bölüm kuralı,${\displaystyle \scriptstyle \varphi '(u)\,{=}\,-u\,\varphi (u)}$ kullanılır.

${\displaystyle {\begin{aligned}{\Bigl (}1+{\frac {1}{x^{2}}}{\Bigr )}Q(x)&=\int _{x}^{\infty }{\Bigl (}1+{\frac {1}{x^{2}}}{\Bigr )}\varphi (u)\,du\\&>\int _{x}^{\infty }{\Bigl (}1+{\frac {1}{u^{2}}}{\Bigr )}\varphi (u)\,du=-{\biggl .}{\frac {\varphi (u)}{u}}{\biggr |}_{x}^{\infty }={\frac {\varphi (x)}{x}}.\end{aligned}}}$

${\displaystyle Q(x)}$çözümü için alt sınır sağlar. Q-fonksiyonunun Chernoff sınırı

${\displaystyle {\begin{aligned}Q(x)\leq {\frac {1}{2}}e^{-{\frac {x^{2}}{2}}},\qquad x>0\end{aligned}}}$

Değerler

Q fonksiyonlu iyi bir tablo ve bu Matlab ve Mathematica gibi matematik yazılım paketleri içinde çoğu doğrudan hesaplanabilir. Q fonksiyonlu bazı değerler referans için aşağıda verilmiştir.

Q(0.0) = 0.500000000 Q(0.1) = 0.460172163 Q(0.2) = 0.420740291 Q(0.3) = 0.382088578 Q(0.4) = 0.344578258 Q(0.5) = 0.308537539 Q(0.6) = 0.274253118 Q(0.7) = 0.241963652 Q(0.8) = 0.211855399 Q(0.9) = 0.184060125

Q(1.0) = 0.158655254 Q(1.1) = 0.135666061 Q(1.2) = 0.115069670 Q(1.3) = 0.096800485 Q(1.4) = 0.080756659 Q(1.5) = 0.066807201 Q(1.6) = 0.054799292 Q(1.7) = 0.044565463 Q(1.8) = 0.035930319 Q(1.9) = 0.028716560

Q(2.0) = 0.022750132 Q(2.1) = 0.017864421 Q(2.2) = 0.013903448 Q(2.3) = 0.010724110 Q(2.4) = 0.008197536 Q(2.5) = 0.006209665 Q(2.6) = 0.004661188 Q(2.7) = 0.003466974 Q(2.8) = 0.002555130 Q(2.9) = 0.001865813

Q(3.0) = 0.001349898 Q(3.1) = 0.000967603 Q(3.2) = 0.000687138 Q(3.3) = 0.000483424 Q(3.4) = 0.000336929 Q(3.5) = 0.000232629 Q(3.6) = 0.000159109 Q(3.7) = 0.000107800 Q(3.8) = 0.000072348 Q(3.9) = 0.000048096 Q(4.0) = 0.000031671

Kaynakça

1. The Q-function, from cnx.org
2. Basic properties of the Q-function
3. Normal Distribution Function - from Wolfram MathWorld