Hata fonksiyonu

hata fonksiyonu çizimi

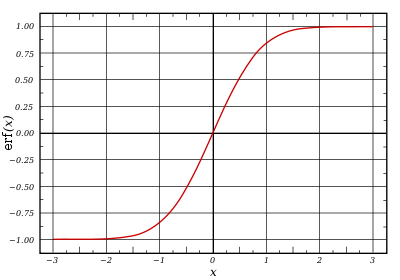
Matematik'te, hata fonksiyonu (ayrıca Gauss hata fonksiyonu olarak da adlandırılır) özel fonksiyon'dur.olasılık, istatistik ve kısmi differansiyel denklem içinde sigmoid ve Temel olmayan bir fonksiyondur . Tanımı :^[1][2]

${\displaystyle \operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t.}$

(Eğer x negatif ise,integralin negatifi xdan sıfıra yorumlanır.)

tamamlayıcı hata fonksiyonu 'nun ifadesi erfcdir.tanımı,

${\displaystyle {\begin{aligned}\operatorname {erfc} (x)&=1-\operatorname {erf} (x)\\&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t.\end{aligned}}}$

Sanal hata fonksiyonu, ifadesi erfi, tanımı,

${\displaystyle \operatorname {erfi} (z)=-i\,\,\operatorname {erf} (i\,z).}$

Karmaşık hata fonksiyonu , ifadesi w(x) ve aynı şekilde Faddeeva fonksiyonu olarak bilinir., tanımı

${\displaystyle w(x)=e^{-x^{2}}{\operatorname {erfc} }(-ix)=e^{-x^{2}}[1+i\,\,\operatorname {erfi} (x)].}$

Özellikleri

Karmaşık düzlemde çizim

Integrand exp(−z²)

erf(z)

özelliği ${\displaystyle \operatorname {erf} (-z)=-\operatorname {erf} (z)}$ hata fonksiyonu başka bir değişle bir tek fonksiyondur.

herhangi bir karmaşık sayı z:

${\displaystyle \operatorname {erf} ({\overline {z}})={\overline {\operatorname {erf} (z)}}}$

burada z 'nin Karmaşık eşleniği ifadesi ${\displaystyle {\overline {z}}}$ dır.

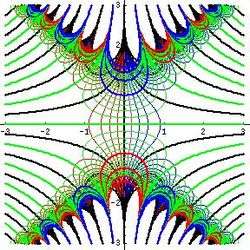
integrandın ƒ = exp(−z²) ve ƒ = erf(z) karmaşık z-düzlemi içinde gösterimi resim 2 ve 3 içindedir. Im(ƒ) = 0 seviyesi kalın yeşil bir çizgi ile gösterilir.Im(ƒ)in Negatif tamsayı değeri kalın kırmızı bir çizgi ile gösterilir.${\displaystyle \Im (f)}$'ın pozitif tamsayı değeri kalın mavi bir çizgi ile gösterilir.sabit ara basamak Im(ƒ) =  ince yeşil çizgi ile gösterilmiştir. Re(ƒ) = sabit ara basamağı negatif değerleri için ince kırmızı çizgi ve pozitif değerleri için ince mavi çizgi.

reel eksen, erf(z) yaklaşım birimi z → +∞ ve −1 at z → −∞. sanal eksenin eğimi ±i∞ a gider.

Taylor serisi

Hata fonksiyonu bir tam fonksiyon'dur; tekillik yoktur(sonsuz hariç) ve Taylor açılımı her halükarda yakınsaktır.

temel fonksiyon içindeki terimlerin kapalı form olarak integrali tanımlanamaz, ama integrand'ın e^−z2 tarafından açılımı Taylor serisi içindedir ve terimleri tarafından integrallenmiş terimlerden, bir Taylor serisinden hata fonksiyonunun elde edilmesi:

${\displaystyle \operatorname {erf} (z)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\ \cdots \right)}$

Her karmaşık sayı z için böyledir. OEIS paydadaki terimler dizisiA007680'dir .

Yukarıdaki serinin ardışık hesaplamaları için,belki şu alternatif yöntem kullanılabilir:

${\displaystyle \operatorname {erf} (z)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}}$

çünkü ${\displaystyle {\frac {-(2k-1)z^{2}}{k(2k+1)}}}$ k^inci içindeki çarpan için açılım ifadesidir. (k + 1)^inci terim ( z göze çarpan ilk terimdir).

Hata fonksiyonu +∞ 'da tam olarak 1 dir (bakınız Gaussian integral).

Hata fonksiyonunun türevi tanımı hemen aşağıda:

${\displaystyle {\frac {\rm {d}}{{\rm {d}}z}}\,\mathrm {erf} (z)={\frac {2}{\sqrt {\pi }}}\,e^{-z^{2}}.}$

hata fonksiyonunun antitürev'i aşağıdadır;

${\displaystyle z\,\operatorname {erf} (z)+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}.}$

Ters fonksiyonu

Ters hata fonksiyonu Maclaurin serisi içindeki terimlerden tanımlanabilir.

${\displaystyle \operatorname {erf} ^{-1}(z)=\sum _{k=0}^{\infty }{\frac {c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},\,\!}$

burada c₀ = 1 ve

${\displaystyle c_{k}=\sum _{m=0}^{k-1}{\frac {c_{m}c_{k-1-m}}{(m+1)(2m+1)}}=\left\{1,1,{\frac {7}{6}},{\frac {127}{90}},\ldots \right\}.}$

Bu yüzden seri açılımı (ortak faktörlerin pay ve paydalarının sadeleştirildiğini unutmayın):

${\displaystyle \operatorname {erf} ^{-1}(z)={\tfrac {1}{2}}{\sqrt {\pi }}\left(z+{\frac {\pi }{12}}z^{3}+{\frac {7\pi ^{2}}{480}}z^{5}+{\frac {127\pi ^{3}}{40320}}z^{7}+{\frac {4369\pi ^{4}}{5806080}}z^{9}+{\frac {34807\pi ^{5}}{182476800}}z^{11}+\cdots \right).\ }$

( pay/payda kesirlerinin sadeleştirilmesi sonrası OEIS içindeki tam olarak A092676/A132467'dır ; pay terimleri sadeleştirme olmadan A002067 çıkışını verir.) Not;hata fonksiyonunun değeri  ±∞ için  ±1'e eşittir.

Ters tamamlayıcı hata fonksiyonunun tanımı;

${\displaystyle \operatorname {erfc} ^{-1}(1-z)=\operatorname {erf} ^{-1}(z).}$

Asimtotik açılım

Büyük x'lar için tamamlayıcı ters hata fonksiyonunun (ve bu nedenle de yine hata fonksiyonunun) yararlı bir asimtotik açılımı'dır.

${\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left[1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{(2x^{2})^{n}}}\right]={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{(2x^{2})^{n}}},\,}$

burada (2n–1)!! çift faktöriyeldir: üst sınır (2n–1) bütün tek fonksiyonların türetilmesi içindir.Her sonlu x sayısı için bu seri yakınsaktır, ve herhangi ${\displaystyle N\in \mathbb {N} }$ için asimtotik açılımın anlamı şudur,

${\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{N-1}(-1)^{n}{\frac {(2n-1)!!}{(2x^{2})^{n}}}+R_{N}(x)\,}$ idi..

buradaki kalan,Landau gösterimi içinde,

${\displaystyle R_{N}(x)=O(x^{-2N+1}e^{-x^{2}})}$ as ${\displaystyle x\to \infty }$'dir.

gerçekten,geriye kalan tam değerdir:

${\displaystyle R_{N}(x):={\frac {(-1)^{N}}{\sqrt {\pi }}}2^{-2N+1}{\frac {(2N)!}{N!}}\int _{x}^{\infty }t^{-2N}e^{-t^{2}}\,\mathrm {d} t,}$

bu indüksiyon yoluyla kolayca,${\displaystyle e^{-t^{2}}=-(2t)^{-1}(e^{-t^{2}})'}$ yazılır ve parçaların integralidir.

sürekli kesirlere açılım

Tamamlayıcı hata fonksiyonunun sürekli kesirlere açılımı ^[3]:

${\displaystyle \mathrm {erfc} (z)={\frac {z}{\sqrt {\pi }}}e^{-z^{2}}{\cfrac {a_{1}}{z^{2}+{\cfrac {a_{2}}{1+{\cfrac {a_{3}}{z^{2}+{\cfrac {a_{4}}{1+\dotsb }}}}}}}}\qquad a_{1}=1,\quad a_{m}={\frac {m-1}{2}},\quad m\geq 2}$

İlişkili fonksiyonlar

Φ ifadesi ile gösterilen standart yığmalı dağılım fonksiyonu'na hata fonksiyonu esasen özdeştir,aynı şekilde yazılım dilinde adı norm(x)'tır. , bunlar farklı olarak sadece ölçeklendirme ve çeviri içindir. gerçekten,

${\displaystyle \Phi (x)={\tfrac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t={\tfrac {1}{2}}\left[1+{\mbox{erf}}\left({\frac {x}{\sqrt {2}}}\right)\right]={\tfrac {1}{2}}\,{\mbox{erfc}}\left(-{\frac {x}{\sqrt {2}}}\right)}$

veya yeniden erf ve erfc için :

${\displaystyle {\begin{aligned}\mathrm {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\\mathrm {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)=2(1-\Phi \left(x{\sqrt {2}}\right)).\end{aligned}}}$

Sonuç olarak, hata fonksiyonu da yakından Q-fonksiyonu ile ilgilidir, bu standart normal dağılımın ard olasılığı,hata-fonksiyonu içindeki Q fonksiyonu terimleriyle ifade edilebilir

${\displaystyle Q(x)={\tfrac {1}{2}}-{\tfrac {1}{2}}\operatorname {erf} {\Bigl (}{\frac {x}{\sqrt {2}}}{\Bigr )}={\tfrac {1}{2}}\operatorname {erfc} ({\frac {x}{\sqrt {2}}}).}$

Normal kantil fonksiyonu olarak bilinen ${\displaystyle \scriptstyle \Phi \,}$ ters fonksiyonu,veya probit fonksiyonu veya belki ters hata fonksiyonu olarak ifade edilebilir.

${\displaystyle \operatorname {probit} (p)=\Phi ^{-1}(p)={\sqrt {2}}\,\operatorname {erf} ^{-1}(2p-1)=-{\sqrt {2}}\,\operatorname {erfc} ^{-1}(2p).}$

Standart normal cdf olasılık ve istatistik daha sık kullanılır, ve hata fonksiyonu matematiğin diğer dallarında daha sık kullanılır.

Mittag-Leffler fonksiyonu hata fonksiyonunun özel bir durumdur , ve konfluent hipergeometrik fonksiyonu olarak da ifade edilebilen (Kummer fonksiyonu):

${\displaystyle \mathrm {erf} (x)={\frac {2x}{\sqrt {\pi }}}\,_{1}F_{1}\left({\tfrac {1}{2}},{\tfrac {3}{2}},-x^{2}\right).}$

Fresnel integrali içerisinde basit bir ifade vardır.Şablon:Elucidate

tamamlanmamış gama fonksiyonu ve Düzgünleştirilmiş Gama fonksiyonu P terimleri içinde ,

${\displaystyle \operatorname {erf} (x)=\operatorname {sgn} (x)P\left({\tfrac {1}{2}},x^{2}\right)={\operatorname {sgn} (x) \over {\sqrt {\pi }}}\gamma \left({\tfrac {1}{2}},x^{2}\right).}$

${\displaystyle \scriptstyle \operatorname {sgn} (x)\ }$ işaret fonksiyonudur.

Temel fonksiyonlar ile yaklaşım

Abramowitz ve Stegun doğruluğu değişen çeşitli yaklaşımları verdi (denklem 7.1.25-28). belirli bir uygulama için uygun en hızlı yaklaşımı seçmesine olanak sağlar. Artan doğruluk için bunlar:

${\displaystyle \operatorname {erf} (x)\approx 1-{\frac {1}{(1+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4})^{4}}}}$    (maximum error: 5·10⁻⁴)

burada a₁=0.278393, a₂=0.230389, a₃=0.000972, a₄=0.078108

${\displaystyle \operatorname {erf} (x)\approx 1-(a_{1}t+a_{2}t^{2}+a_{3}t^{3})e^{-x^{2}},\quad t={\frac {1}{1+px}}}$    (maximum error: 2.5·10⁻⁵)

burada p=0.47047, a₁=0.3480242, a₂=-0.0958798, a₃=0.7478556

${\displaystyle \operatorname {erf} (x)\approx 1-{\frac {1}{(1+a_{1}x+a_{2}x^{2}+...+a_{6}x^{6})^{16}}}}$    (maximum error: 3·10⁻⁷)

burada a₁=0.0705230784, a₂=0.0422820123, a₃=0.0092705272, a₄=0.0001520143, a₅=0.0002765672, a₆=0.0000430638

${\displaystyle \operatorname {erf} (x)\approx 1-(a_{1}t+a_{2}t^{2}+...+a_{5}t^{5})e^{-x^{2}},\quad t={\frac {1}{1+px}}}$    (maximum error: 1.5·10⁻⁷)

burada p=0.3275911, a₁=0.254829592, a₂=−0.284496736, a₃=1.421413741, a₄=−1.453152027, a₅=1.061405429

bu yaklaşımlar x≥0 tümü için geçerlidir. Negatif x'a bu yaklaşımları kullanmak için, Aslında bu erf (x) bir tek fonksiyondur, böylece erf(x)=−erf(−x).

verilen başka bir yaklaşım verilen

${\displaystyle \operatorname {erf} (x)\approx \operatorname {sgn}(x){\sqrt {1-\exp \left(-x^{2}{\frac {4/\pi +ax^{2}}{1+ax^{2}}}\right)}}}$

burada

${\displaystyle a={\frac {8(\pi -3)}{3\pi (4-\pi )}}\approx 0.140012.}$

Burada biri 0'ın komşuluğunda ve biri sonsuz komşuluğunda çok doğru olacak şekilde tasarlanmıştır ve hata, tüm x'lar için 0,00035'ten az hatadır. a ≈ 0.147 alternatif değeri kullanılarak yaklaşık maksimum 0,00012 hata azaltır.^[4]

Bu yaklaşım aynı zamanda ters hata fonksiyonunu hesaplamak için ters çevrildiğinde:

${\displaystyle \operatorname {erf} ^{-1}(x)\approx \operatorname {sgn}(x){\sqrt {{\sqrt {\left({\frac {2}{\pi a}}+{\frac {\ln(1-x^{2})}{2}}\right)^{2}-{\frac {\ln(1-x^{2})}{a}}}}-\left({\frac {2}{\pi a}}+{\frac {\ln(1-x^{2})}{2}}\right)}}}$

Uygulamalar

normal dağılım ile standart sapma tarafından verilen ölçüm serisinin ifadesinin sonuçlarıdır. ${\displaystyle \scriptstyle \sigma }$ ve beklenen değer 0, o zaman pozitif a için −a ve +a ${\displaystyle \scriptstyle \operatorname {erf} \,\left(\,{\frac {a}{\sigma {\sqrt {2}}}}\,\right)}$ tek bir ölçüm arasında yatan hata olasılığıdır.Bu sayısal iletişim sisteminin bit hata oranı'nın belirlenmesinde kullanılan bir örnektir.

oluşan hata ve tamamlayıcı hata fonksiyonları,için örnek,Heaviside basamak fonksiyonu tarafından verilen. ısı denklemi'nin sınır koşulu içindeki çözümüdür.

Genelleştirilmiş hata fonksiyonları

Genelleştirilmiş hata fonksiyonları E_n(x):
gri eğri: E₁(x) = (1 − e ^−x)/${\displaystyle \scriptstyle {\sqrt {\pi }}}$
kırmızı eğri: E₂(x) = erf(x)
yeşil eğri: E₃(x)
mavi eğri: E₄(x)
altın eğri: E₅(x).

Daha genel fonksiyonları bazı yazarlar tartışıyor:

${\displaystyle E_{n}(x)={\frac {n!}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{n}}\,\mathrm {d} t={\frac {n!}{\sqrt {\pi }}}\sum _{p=0}^{\infty }(-1)^{p}{\frac {x^{np+1}}{(np+1)p!}}\,.}$

Çarpıcı örnekleri:

• E₀(x) orijinden düz bir çizgidir: ${\displaystyle \scriptstyle E_{0}(x)={\frac {x}{e{\sqrt {\pi }}}}}$
• E₂(x) hata fonksiyonudur, erf(x).

tek n için n! tarafından bölünme sonrası,bütün E_n benzer (ama aynı değildir) Aynı şekilde,çift n içinn!tarafından bütünE_n için birbirlerine basit bir bölünme sonrası benzer (ama aynı değildir). Tüm genelleştirilmiş hata fonksiyonları içinn > 0 grafiğin pozitif x tarafı birbirine çok benziyor.

Gama fonksiyonu ve tamamlanmamış Gama fonksiyonu kullanılarak x > 0 için bu genelleşmiş fonksiyonların eşdeğerleri ifade edilebilir:

${\displaystyle E_{n}(x)={\frac {\Gamma (n)\left(\Gamma \left({\frac {1}{n}}\right)-\Gamma \left({\frac {1}{n}},x^{n}\right)\right)}{\sqrt {\pi }}},\quad \quad x>0.\ }$

Bu nedenle tamamlanmamış Gama fonksiyonu terimleri içerisindeki hata fonksiyonunu tanımlayabiliriz  :

${\displaystyle \operatorname {erf} (x)=1-{\frac {\Gamma \left({\frac {1}{2}},x^{2}\right)}{\sqrt {\pi }}}.\ }$

Tamamlayıcı hata fonksiyonunun yinelemeli integralleri

Tamamlayıcı hata fonksiyonunun yinelemeli integrallerinin tanımı

${\displaystyle \mathrm {i} ^{n}\operatorname {erfc} \,(z)=\int _{z}^{\infty }\mathrm {i} ^{n-1}\operatorname {erfc} \,(\zeta )\;\mathrm {d} \zeta .\,}$

Burada güç serisi var

${\displaystyle \mathrm {i} ^{n}\operatorname {erfc} \,(z)=\sum _{j=0}^{\infty }{\frac {(-z)^{j}}{2^{n-j}j!\Gamma \left(1+{\frac {n-j}{2}}\right)}}\,,}$

izlediğimiz simetri özelliklerinden

${\displaystyle \mathrm {i} ^{2m}\operatorname {erfc} (-z)=-\mathrm {i} ^{2m}\operatorname {erfc} \,(z)+\sum _{q=0}^{m}{\frac {z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}}}$

ve

${\displaystyle \mathrm {i} ^{2m+1}\operatorname {erfc} (-z)=\mathrm {i} ^{2m+1}\operatorname {erfc} \,(z)+\sum _{q=0}^{m}{\frac {z^{2q+1}}{2^{2(m-q)-1}(2q+1)!(m-q)!}}\,.}$

Uygulamaları

• C: C99 math.h başlığı altında double erf(double x) ve double erfc(double x) sağlar .Bu fonksiyonların çiftleri {erff(),erfcf()} ve {erfl(),erfcl()} alabilir ve ve sırasıyla float ve long double tip değerlerine döndürebilir
• C++: C++11 erf() ve erfc() başlığındaki cmath sağlar buna dayanılarak kabul edilen float, double, ve long double tipi,her iki fonksiyon argumanlarının ötesidir.
• Fortran: Fortran 2008 ERF, ERFC ve ERFC_SCALEDstandard sağlayıcısı fonksiyonların hata fonksiyonu hesabı ve onun tamamlayıcısıdır .
• PERL: erf PERL Module Math::SpecFun uygulamasıdır
• Python:math.erf() olarak 2.7 sürümünden beri dahildir. önceki versiyon erf uygulamaları SciPy içindeki kompleks argüment scipy.special.erf() erf uygulamasıdır.

^[5] ve ayrıca arbitrary-precision arithmetic içinde mpmathmpmath.erf() kütüphanesi içindedir

• Mathematica:Erf ve Erfc in Mathematica içindeki erf uygulamalarıdır.
• Haskell (programlama dili): içinde erf paketi ^[6] hata fonksiyonu hesabı ve yerel kayan nokta türleri için uygulamaları için bir class tipi sağlayan var
• R: "Sözde hata fonksiyonu hesabı'"^[7] is direkt sağlayıcı değildir, amanormal yığılımlı dağılım fonksiyonu detaylıdır. (?pnorm), bir W. J. Cody's temelli rasyonel Chebyshev yaklaşıklığı algoritmasıdır.^[8]
• MathCAD erf(x) ve erfc(x) çiftini sağlar.
• Matlab ayrıca W. J. Cody's algoritması ile erf ve erfc çiftini sağlar.
• Ruby: Math.erf() ve Math.erfc() sağlayıcısı.
• Java: Apache ortak matematik ^[9] erf ve erfc uygulaması sağlayıcısı.
• Google search: Google aramaları ayrıca ve bir "erf(...)" ve "erfc(...)" hesaplayıcısı geliştirecek.

Değerler tablosu

x erf(x) erfc(x) x erf(x) erfc(x) 0.00 0.0000000 1.0000000 1.30 0.9340079 0.0659921 0.05 0.0563720 0.9436280 1.40 0.9522851 0.0477149 0.10 0.1124629 0.8875371 1.50 0.9661051 0.0338949 0.15 0.1679960 0.8320040 1.60 0.9763484 0.0236516 0.20 0.2227026 0.7772974 1.70 0.9837905 0.0162095 0.25 0.2763264 0.7236736 1.80 0.9890905 0.0109095 0.30 0.3286268 0.6713732 1.90 0.9927904 0.0072096 0.35 0.3793821 0.6206179 2.00 0.9953223 0.0046777 0.40 0.4283924 0.5716076 2.10 0.9970205 0.0029795 0.45 0.4754817 0.5245183 2.20 0.9981372 0.0018628 0.50 0.5204999 0.4795001 2.30 0.9988568 0.0011432 0.55 0.5633234 0.4366766 2.40 0.9993115 0.0006885 0.60 0.6038561 0.3961439 2.50 0.9995930 0.0004070 0.65 0.6420293 0.3579707 2.60 0.9997640 0.0002360 0.70 0.6778012 0.3221988 2.70 0.9998657 0.0001343 0.75 0.7111556 0.2888444 2.80 0.9999250 0.0000750 0.80 0.7421010 0.2578990 2.90 0.9999589 0.0000411 0.85 0.7706681 0.2293319 3.00 0.9999779 0.0000221 0.90 0.7969082 0.2030918 3.10 0.9999884 0.0000116 0.95 0.8208908 0.1791092 3.20 0.9999940 0.0000060 1.00 0.8427008 0.1572992 3.30 0.9999969 0.0000031 1.10 0.8802051 0.1197949 3.40 0.9999985 0.0000015 1.20 0.9103140 0.0896860 3.50 0.9999993 0.0000007

x erfc(x)/2 1 0.0786496 2 0.00233887 3 1.10452e-05 4 7.70863e-09 5 7.6873e-13 6 1.07599e-17 7 2.09191e-23 8 5.61215e-30 9 2.06852e-37 10 1.04424e-45 11 7.20433e-55 12 6.78131e-65 13 8.69779e-76 14 1.51861e-87 15 3.6065e-100 16 1.16424e-113 17 5.10614e-128 18 3.04118e-143 19 2.45886e-159 20 2.69793e-176 21 4.01623e-194 22 8.10953e-213 23 2.22063e-232 24 8.24491e-253 25 4.15009e-274 26 2.8316e-296 27 2.61855e-319

Ayrıca bakınız

• Matematiksel fonksiyonların listesi

İlişkili fonksiyonlar

• Gauss integrali, tümüyle gerçek eksen üzerinden
• Gauss fonksiyonu, türev
• Dawson fonksiyonu, ardışık normalleştirmenin hayali hata fonksiyonu

Olasılık içinde

• Normal dağılım
• Normal yığmalı dağılım fonksiyonu,hata fonksiyonu kaymış formu ve bir ölçeği
• Probit, normal CDF'nin ters veya quantile fonksiyon'u
• Q-fonksiyonu,normal dağılımın olasılık eki

Kaynakça

1. Andrews, Larry C.; Special functions of mathematics for engineers
2. Greene, William H.; Econometric Analysis (fifth edition), Prentice-Hall, 1993, p. 926, fn. 11
3. Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2. 
4. Winitzki, Sergei (6 February 2008). "A handy approximation for the error function and its inverse" (PDF). http://sites.google.com/site/winitzki/sergei-winitzkis-files/erf-approx.pdf. Erişim tarihi: 2011-10-03. 
5. http://docs.scipy.org/doc/scipy/reference/generated/scipy.special.erf.html
6. http://hackage.haskell.org/package/erf
7. R Development Core Team (2011-02-25), R: The Normal Distribution, http://stat.ethz.ch/R-manual/R-patched/library/stats/html/Normal.html 
8. Cody, William J. (1969). "Rational Chebyshev Approximations for the Error Function". Math. Comp. 23 (107): 631–637. http://www.ams.org/journals/mcom/1969-23-107/S0025-5718-1969-0247736-4/S0025-5718-1969-0247736-4.pdf. 
9. http://commons.apache.org/math

Dış bağlantılar

• MathWorld – Erf