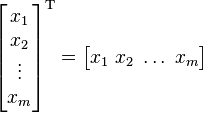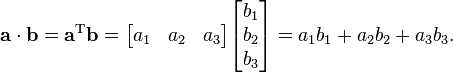Sütun vektör

Doğrusal cebirde sütun vektör veya sütun matris, m × 1 matrisidir. Örneğin; tek bir m sütunundan oluşan bir matris şöyle ifade edilir;

$\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_m \end{bmatrix}$

Bir sütun vektörün transpozesi, satır vektördür, bunun tersi de geçerlidir.

$\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_m \end{bmatrix}^{\rm T} = \begin{bmatrix} x_1 \; x_2 \; \dots \; x_m \end{bmatrix}$

Çift uzay olan bir vektör uzayı ögelerinin sayısı, tüm sütun vektörlerinin kümesini oluşturur.

Gösterim

Sütun vektörlerinin yazımını basitleştirerek satırsal metinlerle ifade etmek için, bazen transpozesi alınarak satır vektörüne dönüştürülür.

$\mathbf{x} = \begin{bmatrix} x_1 \; x_2 \; \dots \; x_m \end{bmatrix}^{\rm T}$

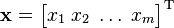
veya

$\mathbf{x} = \begin{bmatrix} x_1, x_2, \dots, x_m \end{bmatrix}^{\rm T}$

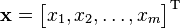
Sütun matrisinin daha da basitleştirmek için bazıları hem satır vektörlerini hem de sütun vektörlerini satır olarak yazarlar. Fakat bu durumda satır vektör ögeleri virgüllerle, sütun vektör ögeleri de noktalı virgüllerle ayrılarak yazılır (aşağıdaki tablodaki alternatif gösterim 2'ye bakın).

	Satır vektör	Sütun vektör
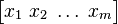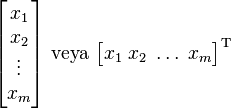Standart matris gösterimi	$\begin{bmatrix} x_1 \; x_2 \; \dots \; x_m \end{bmatrix}$	$\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_m \end{bmatrix} \text{ veya } \begin{bmatrix} x_1 \; x_2 \; \dots \; x_m \end{bmatrix}^{\rm T}$
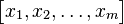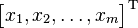Alternatif gösterim 1	$\begin{bmatrix} x_1, x_2, \dots, x_m \end{bmatrix} \qquad$	$\begin{bmatrix} x_1, x_2, \dots, x_m \end{bmatrix}^{\rm T}$
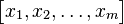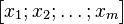Alternatif gösterim 2	$\begin{bmatrix} x_1, x_2, \dots, x_m \end{bmatrix} \qquad$	$\begin{bmatrix} x_1; x_2; \dots; x_m \end{bmatrix}$

İşlemler

• Matris çarpımı, bir matrisin her bir satır vektörlerinin, diğer matrisin her bir sütun vektörleri ile çarpılmasıdır. Bu işlemde sonuçta yine bir matris elde edilir.

• a ve b iki vektörünün nokta çarpımı, a satır vektörünün ögelerinin, b sütun vektörünün ögeleri ile çarpılmasıdır. Sonuçta bir sayı veya değer elde edilir. Aşağıdaki şekilde ifade edilir:

$\mathbf{a} \cdot \mathbf{b} = \mathbf{a}^\mathrm{T} \mathbf{b} = \begin{bmatrix} a_1 & a_2 & a_3 \end{bmatrix}\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}= a_1b_1 + a_2b_2 + a_3b_3.$

Ayrıca bakınız

• Vektörlerin eşdeğişken ve karşıtdeğişkeni