Tanım kümesi
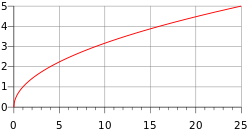
Matematikte verilmiş bir fonksiyonun tanım kümesi, fonksiyonun tanımlı olduğu "girdi" değerlerinin oluşturduğu kümedir.[1] Örneğin, kosinüsün tanım kümesi gerçel sayılar olurken karekök fonksiyonunun tanım kümesi (karmaşık sayılar önemsenmezse) 0 ve 0'dan büyük sayıların oluşturduğu negatif olmayan gerçel sayılar kümesidir. Fonksiyonun xy Kartezyen koordinat sistemindeki temsilinde, tanım kümesi x-ekseni (apsis) ile temsil edilir.
Kesin tanım
Bir f:X→Y fonksiyonu verilmiş olsun. Girdi değerlerinin oluşturduğu X kümesi f 'nin tanım kümesi iken; Y kümesi ise f 'nin değer kümesidir.
f 'nin görüntü kümesi ise f 'nin bütün çıktı değerlerinin kümesidir; yani kümesidir.[2] f nin görüntü kümesi değer kümesi ile aynı küme olabilir veya değer kümesinin bir altkümesi olabilir. f örten fonksiyon olmadıkça genelde değer kümesinden daha küçük bir kümedir.
İyi tanımlı bir fonksiyon tanım kümesindeki her elemanı değer kümesindeki bir elemana göndermelidir. Mesela,
- f(x) = 1/x
biçiminde tanımlanan fonksiyonun f(0) için bir değeri yoktur. Bu sebeple, gerçel sayılar kümesi , bu fonksiyonun tamın kümesi olamaz. Bu gibi durumlarda, fonksiyon ya üzerinde tanımlanır ya da f(0) açık bir şekilde tanımlanarak "açık yamanır". Eğer f fonksiyonu
- f(x) = 1/x, x ≠ 0
- f(0) = 0,
şeklinde genişletilip tanımlanırsa, o zaman f tüm gerçel değerler için tanımlı olur ve tanım kümesi de olur.
Herhangi bir fonksiyon kendi tanım kümesinin bir altkümesine sınırlandırılabilir. S ⊆ A ise, g : A → B 'nin S 'ye sınırlandırılması g |S : S → B şeklinde yazılır.
Ayrıca bakınız
Kaynakça
- ↑ Paley, H. Abstract Algebra, Holt, Rinehart and Winston, 1966 (s. 16).
- ↑ Smith, William K. Inverse Functions, MacMillan, 1966 (s. 8).