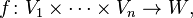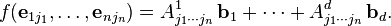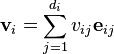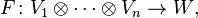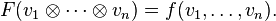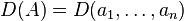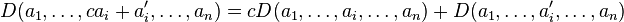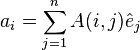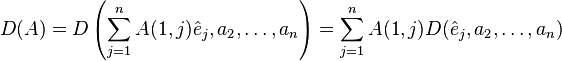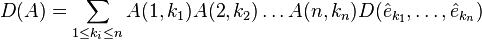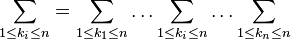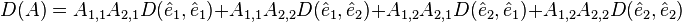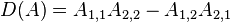Çokludoğrusal harita
Çokludoğrusal cebir veya daha genel olarak doğrusal cebirde, bir çokludoğrusal harita her değişken içinde ayrı ayrı doğrusal birkaç değişkenin bir fonksiyondur. Daha kesin olarak, çokludoğrusal harita şöyle bir fonksiyondur:
burada 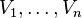 ve
ve 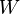 , tüm
, tüm 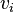 değişkenleri sabit tutulan her
değişkenleri sabit tutulan her 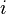 için, aşağıdaki özellikleri sağlayan vektör uzayları (veya modülleri) oluyorsa,
için, aşağıdaki özellikleri sağlayan vektör uzayları (veya modülleri) oluyorsa, 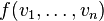 ifadesi
ifadesi 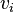 'nin bir doğrusal fonksiyonudur.
'nin bir doğrusal fonksiyonudur.
İki değişkenin bir çokludoğrusal haritası bir çiftdoğrusal haritadır. Daha genel bir ifade ile, k değişkeninin bir çokludoğrusal haritası k-doğrusal harita olarak adlandırılır. Eğer bir çokludoğrusal haritanın ko-domeni, skalerin alanı ise o bir çokludoğrusal form olarak adlandırılır. Çokludoğrusal haritalar ve çokludoğrusal formlar çokludoğrusal cebrin çalışmasında temel nesnedir.
Tüm değişkenler aynı alana ait ise, k-doğrusal haritası için, simetrik, antisimetrik ve alternatizasyon kavramlarından bahsedilebilir.
Örnekler
- Her bir çiftdoğrusal harita bir çokludoğrusal haritadır. Örneğin, bir vektör uzayındaki herhangi bir iç çarpım uzayı bir çokludoğrusal haritadır,
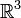 içinde çapraz çarpım vektörleri elde edilir.
içinde çapraz çarpım vektörleri elde edilir. - Bir matrisin determinantı, bir kare matrisin sütunlarının (veya satırlarının) antisimetrik çokludoğrusal fonksiyonudur.
- Eğer
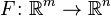 bir Ck fonksiyonu ise,
bir Ck fonksiyonu ise, 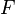 'nin her
'nin her 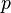 noktasındaki
noktasındaki 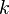 inci türevinde
inci türevinde 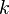 -doğrusal fonksiyon
-doğrusal fonksiyon 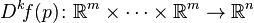 simetrik olarak görülebilir.
simetrik olarak görülebilir. - Çokludoğrusal altuzay öğrenimindeki vektöre-tensör izdüşümü de bir çokludoğrusal haritadadır.
Koordinat gösterimi
Diyelimki
sonlu boyutlu vektör uzayları arasında bir çokludoğrusal haritası olsun. Burada 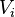 boyutu
boyutu 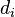 'dir ve
'dir ve 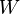 boyutu
boyutu 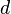 'dir. Her bir
'dir. Her bir 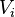 için
için 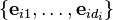 ve
ve 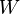 için
için 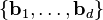 taban seçersek,
taban seçersek, 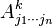 skalerlerini şöyle ifade edebiliriz:
skalerlerini şöyle ifade edebiliriz:
Ardından 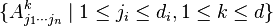 skalerleri,
skalerleri, 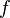 çokludoğrusal fonksiyonunu tam olarak tanımlar.
çokludoğrusal fonksiyonunu tam olarak tanımlar.
Özel olarak eğer,
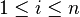 için,
için,
oluyorsa,
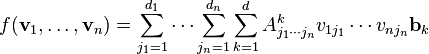 olur.
olur.
Tensör çarpımıyla ilişkisi
Burada, çokludoğrusal haritalar arasında doğal bire-bir karşılaştırma yapılmıştır.
ve doğrusal haritalar
burada 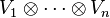 ifadesi
ifadesi 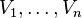 tensör çarpımıdır.
tensör çarpımıdır.
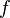 ve
ve 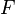 fonksiyonlar arası ilişki şu formül ile verilir:
fonksiyonlar arası ilişki şu formül ile verilir:
n×n matrislerindeki çokludoğrusal fonksiyonlar
Bir K değişmeli halkasındaki n×n matrisindeki çokludoğrusal fonksiyonlar, matrisin satırları (veya eşdeğer sütunları) olarak ifade edilir. Diyelim ki A gibi bir bir matris ve 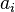 , Anın 1 ≤ i ≤ n aralığındaki satırları olsun. Bu durumda D çokludoğrusal fonksiyonu şöyle yazılabilir:
, Anın 1 ≤ i ≤ n aralığındaki satırları olsun. Bu durumda D çokludoğrusal fonksiyonu şöyle yazılabilir:
Daha geniş bir ifade ile;
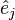 ifadesini, tanım matrisinin j.inci satırı olarak ele alırsak, her bir
ifadesini, tanım matrisinin j.inci satırı olarak ele alırsak, her bir 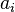 satırını şöyle olur.
satırını şöyle olur.
Dnin çokludoğrusallığı kullanılarak D(A) yı yeniden yazalım;
Her 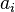 için 1 ≤ i ≤ aralığında sürekli yerine konulursa,
için 1 ≤ i ≤ aralığında sürekli yerine konulursa,
Burada seçtiğimiz 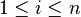 aralığında;
aralığında;
İç içe toplamlar serisi elde edilir.
Burada, 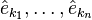 satırlarında
satırlarında 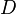 fonksiyonu vasıtasıyla D(A)'nın nasıl elde edildiği görüldü.
fonksiyonu vasıtasıyla D(A)'nın nasıl elde edildiği görüldü.
Örnekler
2×2 matrisleri şöyle yazılır;
Burada ![\hat{e}_1 = [1,0]](../I/m/db13f2660f108606149b2c775e2cf8af.png) ve
ve ![\hat{e}_2 = [0,1]](../I/m/e14388731e6872aa7de3210bc172f421.png) 'dir. D'yi bir alternatif fonksiyon olarak sınırlandırırsak;
'dir. D'yi bir alternatif fonksiyon olarak sınırlandırırsak;
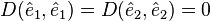 ve
ve 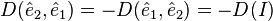 olur.
olur. 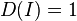 olursa, 2×2 matrisinde şu determanant fonksiyonunu elde ederiz:
olursa, 2×2 matrisinde şu determanant fonksiyonunu elde ederiz:
Özellikler
Çokludoğrusal haritada bir sıfır değeri varsa, bağımsız değişkenlerden biri sıfır olur.
n>1 için, yalnızca n-doğrusal harita ve sıfır fonksiyonudur. Çifte doğrusallık#Örneklere bakınız.
Ayrıca bakınız
- Cebirsel form
- Çokludoğrusal form
- Homojen polinom
- Homojen fonksiyon
- Tensörler
- çoklu doğrusal izdüşüm
- Çokludoğrusal altuzay öğrenimi