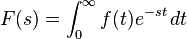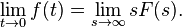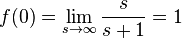Başlangıç değer teoremi
Matematiksel analizde başlangıç değer teoremi, frekans domeni ile ilgili bir ifadenin zaman domenindeki davranışının sıfıra yakınsak zamandaki karşılığı olan bir teoremdir.
Yukarıdaki denklem ƒ(t) fonksiyonunun (tek taraflı) Laplace dönüşümü olsun. Başlangıç değer teoremi şöyle olur;
Örnek
-
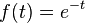 olsun.
olsun. -
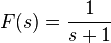
Ayrıca bakınız
This article is issued from Vikipedi - version of the 4/6/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.