Z-dönüşümü
Z dönüşümü, matematikte ve işaret işlemede bir dönüşüm. Zaman tanım kümesinde gerçel ve sanal bileşenleri olan herhangi bir ayrık işareti, frekans tanım kümesindeki biçimine dönüştürür.
Tanım
Dönüşüm şu şekildedir:
Yukarıdaki bağıntıda, n'ler tamsayı ve küçük z'ler karmaşık sayıdır.
Bu ikinci bağıntıya göre ise A, z'nin genliği, φ de fazı ya da argümanı olarak tanımlanır. Faz, radyan'la ölçülür.
Fourier dönüşümü ile ilişkisi
Ayrık zamanlı Fourier dönüşümü (DTFT)'in genelleştirilmesi olan z-dönüşümünün Fourier dönüşümü ile yakından ilgisi vardır. 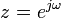 gibi düşünülürse (DTFT) elde edilmektedir. Bunun sebebi şöyle açıklanmaktadır: z bir kompleks sayıdır ve kutupsal formda
gibi düşünülürse (DTFT) elde edilmektedir. Bunun sebebi şöyle açıklanmaktadır: z bir kompleks sayıdır ve kutupsal formda 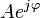 olarak gösterilmektedir. Eğer A = 1 ise z dönüşümü Fourier dönüşümü olmaktadır ama yarıçap 1'den farklı ise o zaman z dönüşümü olarak kalmaktadır.[1]
olarak gösterilmektedir. Eğer A = 1 ise z dönüşümü Fourier dönüşümü olmaktadır ama yarıçap 1'den farklı ise o zaman z dönüşümü olarak kalmaktadır.[1]
ROC, z Dönüşümünün en önemli kavramıdır. ROC (region of convergence-yakınsama bölgesi) bir sinyalin z-dönüşümünün sonsuz olmayan bir sayıya yakınsadığı değerlerinin z-düzlemi üzerinde gösterildiği alandır. ROC sistem hakkında birçok bilgi almamızı sağlar. Çizimi ise aşağıdaki özelliklere bakılarak yapılır.
ROC bir halka ya da bir disktir ve merkezi orjindedir.
H(z)'de z yerine 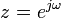 koyulunca Fourier dönüşümüne yakınsayabilmesi için ROC'un birim çemberi içermesi gerekir. Bu aynı zamanda sistemin kararlılık kriteridir. ROC kutup içeremez.
koyulunca Fourier dönüşümüne yakınsayabilmesi için ROC'un birim çemberi içermesi gerekir. Bu aynı zamanda sistemin kararlılık kriteridir. ROC kutup içeremez.
x[n] sınırlı dizi ise ROC bütün z-düzlemidir. Belki 0'ı ya da sonsuzu içermeyebilir.
Nedensel sistemlerde, x[n] sağa yaslıdır ve ROC en dıştaki kutbun dışına doğru olur. Nedensel olmayan sistemlerde, x[n] sola yaslı ve ROC en içteki kutbun içine doğru olur. x[n] hem nedensel hem de anti-nedensel terimler içeriyorsa, ROC en dıştaki kutuptan içeri en içteki kutuptan dışarı doğru olan bir halkadır.
Sistemin hem nedensel hem de kararlı olması durumunda, bütün kutuplar birim çemberin içinde olmalıdır. Çünkü eğer bir kutup bile birim çemberin dışında olsa, nedensel sistem özelliğinden dolayı ROC en sağdaki kutbun dışına doğru olur ve birim çemberi içeremez, bu durumda sistemin kararlılık kriteri de karşılanamaz.
ROC bağlantılı olmak zorundadır.
Bazı Z-dönüşümü çiftleri
Aşağıdaki tabloda bazı sistemlerin z dönüşümleri verilmiştir.
Dirac delta fonksiyonu ve Heaviside birim basamak fonksiyonu aşağıdaki gibi tanımlanır:
Sinyal, ![x[n]](../I/m/d3baaa3204e2a03ef9528a7d631a4806.png) | Z-dönüşümü, 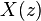 | ROC | |
|---|---|---|---|
| 1 | ![\delta[n] \,](../I/m/2b63622fadf95b2200b264909054224f.png) | 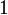 | 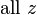 |
| 2 | ![\delta[n-n_0] \,](../I/m/4c035051ef51cb09d5cbe903b496208a.png) | 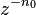 | 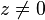 |
| 3 | ![u[n] \,](../I/m/7016daf9693a54fbb365146aa38d73c6.png) | 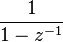 | 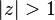 |
| 4 | ![\, e^{-\alpha n} u[n]](../I/m/35097e6a8b51f48e543bf37957ed6d68.png) | 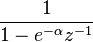 | 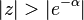 |
| 5 | ![- u[-n-1] \,](../I/m/596e922d21a3ca551fb1805ce332759e.png) | 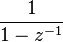 | 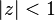 |
| 6 | ![n u[n] \,](../I/m/1654b58cc296812ba337d3753898834b.png) | 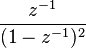 | 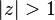 |
| 7 | ![- n u[-n-1] \,](../I/m/41b866b5f12cc275d702937c3a929222.png) | 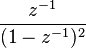 | 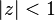 |
| 8 | ![n^2 u[n] \,](../I/m/3d24a549af9143a2482c7d169e135795.png) | 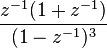 | 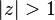 |
| 9 | ![- n^2 u[-n - 1] \,](../I/m/78282ba68d8f36a1586b3247cbdd5674.png) | 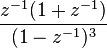 | 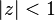 |
| 10 | ![n^3 u[n] \,](../I/m/40044ac2551be5de950fc05a4fbcb30f.png) | 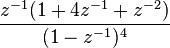 | 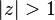 |
| 11 | ![- n^3 u[-n -1] \,](../I/m/6f1d679d09c86f67ae88195f6307fde6.png) | 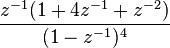 | 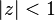 |
| 12 | ![a^n u[n] \,](../I/m/52005e1c22b667a92f6a7f8763d198aa.png) | 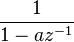 | 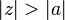 |
| 13 | ![-a^n u[-n-1] \,](../I/m/5b1d6d741e4466bd975e49b8a7502a06.png) | 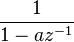 | 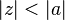 |
| 14 | ![n a^n u[n] \,](../I/m/a5ee7e0b460ced4724323abe028b7d5f.png) | 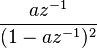 | 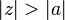 |
| 15 | ![-n a^n u[-n-1] \,](../I/m/5422993372c0c804ccdc7c6d3f62c7b0.png) | 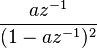 | 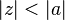 |
| 16 | ![n^2 a^n u[n] \,](../I/m/5e752df8b1b2c1be5b169617d3d885e8.png) | 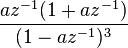 | 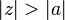 |
| 17 | ![- n^2 a^n u[-n -1] \,](../I/m/2af9e2fbcb9952df47812c829b6477d9.png) | 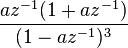 | 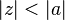 |
| 18 | ![\cos(\omega_0 n) u[n] \,](../I/m/57a085c1d96479f7dd14f6f3d76e0520.png) | 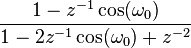 | 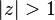 |
| 19 | ![\sin(\omega_0 n) u[n] \,](../I/m/15b15b84c75d60afebabb9fc0c8acb51.png) | 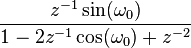 | 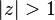 |
| 20 | ![a^n \cos(\omega_0 n) u[n] \,](../I/m/4b8b31d851e269a8a0a415d02a5b9b11.png) | 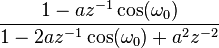 | 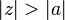 |
| 21 | ![a^n \sin(\omega_0 n) u[n] \,](../I/m/4fb89703f52df7f80a40801273ed980e.png) | 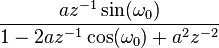 | 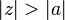 |
Özellikler
| zaman bölgesi | Z- bölgesi | İspat | ROC | |
|---|---|---|---|---|
| Notasyon | ![x[n]=\mathcal{Z}^{-1}\{X(z)\}](../I/m/ac2e4e0332cbbe3296dd601c898b14cf.png) |
![X(z)=\mathcal{Z}\{x[n]\}](../I/m/949157e85e0059c0ef07f00c2c26bc2e.png) |
ROC: 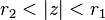 | |
| Doğrusallık | ![a_1 x_1[n] + a_2 x_2[n]\](../I/m/79bdec3451b8f328c4460e35b821b8ea.png) |
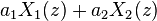 |
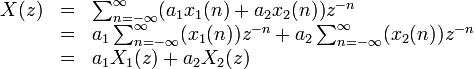 |
En azından ROC1 ve ROC2 bölgelerinin kesişimi |
| Zamanda genişleme | ![x_{(k)}[n] = \begin{cases} x[r], & n = rk \\ 0, & n \not= rk \end{cases}](../I/m/48f5fea0a96a642423ad90e209a52e6b.png)
|
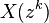 |
R^{1/k} | |
| Zamanda kayma | ![x[n-k]\](../I/m/eb62e81664b3d3f149e9c52f2df4a09b.png) |
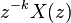 |
![\begin{array} {lcl} Z\{x[n-k]\} &=& \sum_{n=0}^{\infty} x[n-k]z^{-n} \text{ , let }j = n - k\\
&=& \sum_{j=-k}^{\infty} x[j]z^{-(j+k)}\\
&=& \sum_{j=-k}^{\infty} x[j]z^{-j}z^{-k}\\
&=& z^{-k}\sum_{j=-k}^{\infty}x[j]z^{-j}\\
&=& z^{-k}\sum_{j=0}^{\infty}x[j]z^{-j} \text{ , since }x[\beta]=0 \text{ if }\beta<0\\
&=& z^{-k}X(z)\\
\end{array}](../I/m/2960d630fbd07063d0abe5130900453c.png) |
ROC, eğer 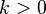 ise dışında ise dışında 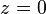 ve eğer ve eğer 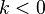 ise ise 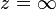 dışında dışında |
| Scaling in the z-domain | ![a^n x[n]\](../I/m/5bc0cde4af5f3bb27463af9a62dc9a20.png) |
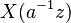 |
![\begin{array} {lcl} Z \{a^n x[n]\} &=& \sum_{n=-\infty}^{\infty} a^{n}x(n)z^{-n} \\ & = &
\sum_{n=-\infty}^{\infty} x(n)(a^{-1}z)^{-n} \\ & = &
X(a^{-1}z)
\end{array}](../I/m/b3afa7afa4cdb4fb700cc7beef32fb95.png) |
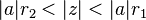 |
| Time reversal | ![x[-n]\](../I/m/daffc5bc57063f1d1bc403656e2d6096.png) |
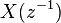 |
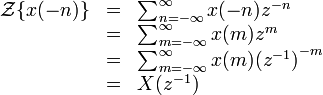 |
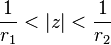 |
| Karmaşık eşlenik | ![x^*[n]\](../I/m/af74a1c4213dafcf6395eeb45e9ac8d2.png) |
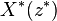 |
![\begin{array} {lcl}Z\{x^*(n)\} & = & \sum_{n=-\infty}^{\infty} x^*(n)z^{-n}\ \\ & = &
\sum_{n=-\infty}^{\infty} [x(n)(z^*)^{-n}]^*\ \\ & = &
[ \sum_{n=-\infty}^{\infty} x(n)(z^*)^{-n}\ ]^* \\ & = &
X^*(z^*)\end{array}](../I/m/6d6185ccbf69ce20377fa66eda19aa94.png) |
ROC |
| Reel kısım | ![\operatorname{Re}\{x[n]\}\](../I/m/7fa84bf49517a5bdb652bcfd0f8a7419.png) |
![\frac{1}{2}\left[X(z)+X^*(z^*) \right]](../I/m/f11b75b76a9c8fbf3b90f47799e92b92.png) |
ROC | |
| Imajiner kısım | ![\operatorname{Im}\{x[n]\}\](../I/m/9d79da92f4c39771f2fc49371473527a.png) |
![\frac{1}{2j}\left[X(z)-X^*(z^*) \right]](../I/m/b3e01ee80092b499fcdeeed27f5f358d.png) |
ROC | |
| Türev | ![nx[n]\](../I/m/d8b2e4a3a8c01427adf3b5a3159cd6aa.png) |
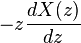 |
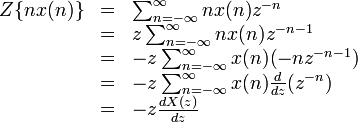 |
ROC |
| Convolution | ![x_1[n] * x_2[n]\](../I/m/84306084618dd955215d355316dbd034.png) |
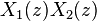 |
![\begin{array} {lcl}\mathcal{Z}\{x_1(n)*x_2(n)\} & = &
\mathcal{Z} \{\sum_{l=-\infty}^{\infty} x_1(l)x_2(n-l)\}\ \\ & = &
\sum_{n=-\infty}^{\infty} [\sum_{l=-\infty}^{\infty} x_1(l)x_2(n-l)]z^{-n}\ \\ & = &
\sum_{l=-\infty}^{\infty} x_1(l) \sum_{n=-\infty}^{\infty} x_2(n-l)z^{-n} ]\ \\ & = &
[\sum_{l=-\infty}^{\infty} x_1(l)z^{-l}] [\sum_{n=-\infty}^{\infty} x_2(n)z^{-n} ]\ \\ & = &
X_1(z)X_2(z)\end{array}](../I/m/a9125d9213f929b34be1b4d799735f58.png) |
en azından ROC1 ve ROC2 keşisim kümesi |
| Correlation | ![r_{x_1,x_2}(l)=x_1[l] * x_2[-l]\](../I/m/2af0b290d13fa5a85e4a60037004ee16.png) |
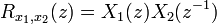 |
en azından X1(z)'e ait ROC ve X2(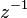 )'e ait ROC'un keşisimi. )'e ait ROC'un keşisimi. | |
| First Difference | ![x[n] - x[n-1] \](../I/m/aa6030ba7dce7f2b8e7fb99082042066.png) |
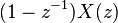 |
En azından X1(z) ve  keşisimi keşisimi | |
| Accumulation | ![\sum_{k=-\infty}^{n} x[k]\](../I/m/5f3de91aaf3bbc0a76508a92c7b4633a.png) |
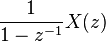 |
![\begin{array} {lcl}\sum_{n=-\infty}^{\infty}\sum_{k=-\infty}^{n} x[k]\cdot z^{-n}\\
=\sum_{n=-\infty}^{\infty}(x[n]+x[n-1]+x[n-2]\cdots x[-\infty])z^{-n}\\
=X[z](1+z^{-1}+z^{-2}+z^{-3}\cdots )\\
=X[z]\sum_{j=0}^{\infty}z^{-j} \\
=X[z] \frac{1}{1-z^{-1}}\end{array}](../I/m/22555d2b79e55e4ff0618513691cf73b.png) |
|
| Çarpma | ![x_1[n]x_2[n]\](../I/m/bd176884c506fcef3604fd6d23de884b.png) |
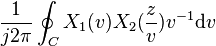 |
- | |
| Parseval teoremi | ![\sum_{n=-\infty}^{\infty} x_1[n]x^*_2[n]\](../I/m/7c33541ee039439ee2a60d83ad93a0dd.png) |
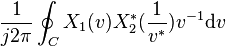 |
- İlk değer teoremi
![x[0]=\lim_{z\rightarrow \infty}X(z) \](../I/m/92bb0bebca1839c58a88b6feff81c6aa.png) , Eğer
, Eğer ![x[n]\,](../I/m/b0f955b87baf7377b98b47ed9c723949.png) nedensel ise.
nedensel ise.
-
![x[\infty]=\lim_{z\rightarrow 1}(z-1)X(z) \](../I/m/79f8f3555de2eba7269fee2a2ca98dc9.png) , Sadece kutuplar
, Sadece kutuplar 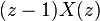 birim çemberin içindeyse.
birim çemberin içindeyse.
-
![X(z) = \mathcal{Z}\{x[n]\} = \sum_{n=-\infty}^{\infty} x[n] z^{-n}](../I/m/4799f830eb930ecb74fe5368df6d7ab6.png)
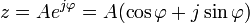
![u[n] = \begin{cases} 1, & n \ge 0 \\ 0, & n < 0 \end{cases}](../I/m/ebaeed1cdf2a16626315fbb5684b3552.png)
![\delta[n] = \begin{cases} 1, & n = 0 \\ 0, & n \ne 0 \end{cases}](../I/m/af1026c1cbf08b31325071a939cf0c07.png)
 : tamsayı
: tamsayı