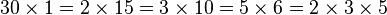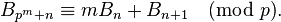Bell sayısı

Matematiğin kombinatorik dalında, the ninci Bell sayısı, n eleman'lı bir küme'nin altküme sayısını verir, veya eşdeğeri, benzerlik ilişkisi'dir. B₀ = B₁ = 1 ile başlar, ilk birkaç Bell sayısı şunlardır:

1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, … ^[1].

Adını Eric Temple Bell'den almıştır.

Bir kümenin alt kümeleri

Genji'nin masalları geleneksel japon sembolleri ile beş element tarafından 52 yola ayrılmıştır.

Genel olarak, B_n n 'inci altküme sayısıdır . A partition of a set S ile gösterilen kümenin altkümesi boşküme değildir. örneğin, B₃  = 5'tir,çünkü the 3-elemanlı küme {a, b, c}'nin 5 alt kümesi vardır:

{ {a}, {b}, {c} }

{ {a}, {b, c} }

{ {b}, {a, c} }

{ {c}, {a, b} }

{ {a, b, c} }.

B₀ 1'dir. burada tam olarak bu kümenin bir alt kümesi boş küme'dir. boş küme olmayan herkümenin bir alt kümesi boş kümedir (bu bir boşluklu gerçek)'tir, ve burada boş küme tektir.. Bundan dolayı,boş küme kendi kendinin altkümesidir.

Unutmadan, küme gösterimi hakkında önerimiz, Kümelerin düzenini veya elemaların kendi içindeki düzenini dikkate almıyoruz. Bu aşağıdaki bölünmelerin tümünün özdeş olduğu anlamına gelir:

{ {b}, {a, c} }

{ {a, c}, {b} }

{ {b}, {c, a} }

{ {c, a}, {b} }.

Çarpanlara ayırma

Eğer bir kare olmayansayı bir N sayısı (bazı n sayı farklı asal sayılar çarpımıdır anlamına gelir ), ise B_n Nin farklı çarpan parçası'nın sayısını verir . Bu sayılar, bir N in çarpanlara ayırma halinden fazla bulunmaktadır onlar farklı bir sırada aynı faktörler varsa,aynı iki çarpanlarına ayırma işlemi görür. ^[2]. Örneğin,30 üç asal 2, 3 çarpımıdır, ve 5 ve beş çarpanlama vardır:

$30\times 1=2\times 15=3\times 10=5\times 6=2\times 3\times 5$

Kafiye şeması

Bell numaraları bir n satır şiir veya dörtlükte kafiye düzeni saymak gibidir .Bir kafiye şeması satırları birbirleri ile kafiyelidir, ve bu nedenle kafiye alt kümeleri çizgi kümesini hangi bir bölümü olarak yorumlanabileceğini açıklar,her bir satır,birbirlerine aynı harf verilen kafiye satırları ve alfabetik olarak etiketli her kafiye kümesinde ilk satırları ile,Kafiye düzenleri genellikle Roma harflerinin dizisi olarak yazılır.Böylece, 15 olası dört satırlık kafiye düzenleri AAAA, AAAB, AABA, AABB, AABC, ABAA, ABAB, ABAC, ABBA, ABBB, ABBC, ABCA, ABCB, ABCC ve ABCD.^[3]

Bell sayılarına diğer bir bakış

Bell sayıları gösterilebilir : şöyleki n sayısı ayırtedilebilir bir veya daha çok sayıda toplar olsun ayırt edilemez kutuların içine farklı olasılıkta yolla yerleştiriyoruz .örneğin, kolaylık olsun n 3'tür.Bizim üç topumuz var, Biz bunlara a, b, ve c diyelim, ve üç kutu var. Kutuların içinde hiçbiri diğerinden farklı değilse,beş farklı yolla topları kutulara yerleştirebiliriz.:

Her topu kendi kutusuna gider.

Her üç top bir kutuya gider.

Yani kutular anonim, bu sadece bir kombinasyon olarak kabul edilir.

a bir kutuya gider, b ve c bir başka kutuya gider.

b Bir kutuya gider a ve c başka bir kutuya gider.

c Bir kutuya gider a ve b başka bir kutuya gider.

Özellikler

Moduler aritmetik

Bell sayıları Touchard'ın eşleşimine uyar: Eğer p herhangi asal sayı ise

$B_{p+n}\equiv B_n+B_{n+1} \pmod{p}$

veya, genelleme

$B_{p^m+n}\equiv mB_n+B_{n+1} \pmod{p}.$

Çünkü Touchard eşleşiminin,Bell sayıları periyodik modulü pdir,her p asal sayısı için ; örneğin, p = 2 için,Bell sayılarının tek-tek-çift periyodik üçlüsü ile desen tekrar ediyor. bu tekrarlı periyot,keyfi bir p asal sayısı için,

$\frac{p^p-1}{p-1}$'nin bir böleni olmalı

ve 101'e kadar tüm p asal sayısı için bu tam asaldır.^[4]

Ayrıca bakınız

• Bell polinomları
• Bell sayılarının sırası - az düzenli sayılar
• İkincil tür Stirling sayıları -n elemanlı k tane boş olmayan kümeli bir kümenin bölünmesinin yollarının sayıları.
• Touchard polinomları

Kaynakça

1. Breakdown by number of subsets/equivalence classes.
2. Williams (1945) credits this observation to Silvio Minetola's Principii di Analisi Combinatoria (1909).
3. Gardner (1978).
4. Williams (1945); Wagstaff (1996).

• Gian-Carlo Rota, 1964, "The Number of Partitions of a Set," American Mathematical Monthly 71(5): 498—504.
• Lovász, L. Combinatorial Problems and Exercises, 2nd ed. Amsterdam, Netherlands: North-Holland, 1993.

Dış bağlantılar

• Diagrams of Bell numbers.
• Using the Bell Triangle to calculate Bell numbers.
• Bell Number at MathWorld.
• The period of the Bell numbers modulo a prime