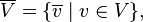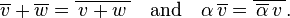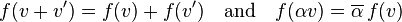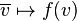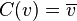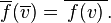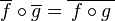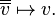Karmaşık eşlenik vektör uzayı
matematikte, bir karmaşık vektör uzayı 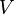 'nın (resmi) karmaşık eşlenik karmaşık vektör uzayı
'nın (resmi) karmaşık eşlenik karmaşık vektör uzayı 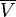
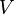 'nin ögelerinin tüm resmi karmaşık eşlenikleri oluşturur. Bu,
'nin ögelerinin tüm resmi karmaşık eşlenikleri oluşturur. Bu, 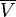 bir vektör uzayı olan ögeleri
bir vektör uzayı olan ögeleri 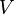 'nın bir-e-bir karşılık içinde ögeleri ile:
'nın bir-e-bir karşılık içinde ögeleri ile:
toplam ve skaler çarpım için aşağıdaki kurallar ile:
Burada  and
and 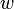
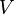 içindeki vektörlerdir,
içindeki vektörlerdir, 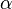 bir karmaşık sayıdır, ve
bir karmaşık sayıdır, ve 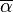 ,
, 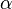 'nın karmaşık eşlenik ifadesidir.
'nın karmaşık eşlenik ifadesidir.
Daha somut,karmaşık eşlenik vektör uzayı gerçek vektör uzayı altta yatan aynı(noktaların aynı kümesi, aynı vektör toplamı ve gerçek skaler çarpım) ile eşlenik doğrusal karmaşık yapı J (iile fark çarpımı)dir.
Antilineer haritalar
Eğer 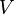 ve
ve 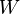 karmaşık vektör uzayı, bir fonksiyon
karmaşık vektör uzayı, bir fonksiyon 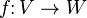 antilineerdir eğer
antilineerdir eğer
tüm 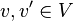 için ve
için ve 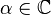 .
.
vektör uzayı 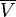 oluşmasına tek neden bu doğrusal göndermeler içinde antilineer göndermeler yapılıyor. Özellikle, eğer
oluşmasına tek neden bu doğrusal göndermeler içinde antilineer göndermeler yapılıyor. Özellikle, eğer 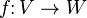 bir antilineer gönderme, ise karşılık gelen gönderme
bir antilineer gönderme, ise karşılık gelen gönderme 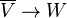 ile tanımlanıyor
ile tanımlanıyor
doğrusaldır. Tersine, herhangi doğrusal gönderme 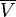 üzerinde tanımlanıyor
üzerinde tanımlanıyor 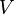 üzerinde bir antilineer göndermeye yükseltme veriliyor.
üzerinde bir antilineer göndermeye yükseltme veriliyor.
Tek yol bu karşılık hakkında düşüncenin bu 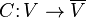 gönderme tanımı ile
gönderme tanımı ile
bir antilineer tanımlansın. Böylece eğer 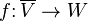 doğrusal, ise bileşim
doğrusal, ise bileşim 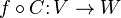 antilineerdir, ve tersi.
antilineerdir, ve tersi.
Doğrusal gönderme eşleniği
Herhangi doğrusalharita 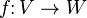 bir eşlenik doğrusal gönderme uyarıyor
bir eşlenik doğrusal gönderme uyarıyor 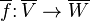 ,formülü ile tanımlanır
,formülü ile tanımlanır
Eşlenik doğrusal gönderme 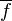 doğrusaldır.Dahası,
doğrusaldır.Dahası, 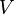 üzerinde özdeş gönderme
üzerinde özdeş gönderme 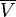 özdeş göndermesini uyarır, ve
özdeş göndermesini uyarır, ve
herhangi iki doğrusal haritalar 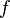 ve
ve 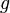 için.Bunun için,
için.Bunun için, 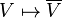 kuralı ve
kuralı ve 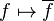 kendisine karmaşık vektör uzayının kategoriden bir funktör tanımlanır.
kendisine karmaşık vektör uzayının kategoriden bir funktör tanımlanır.
Eğer 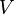 ve
ve 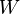 sonlu-boyutlu ve
sonlu-boyutlu ve 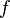 gönderme
gönderme 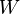 'nin
'nin 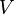 ve
ve 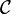 sinin taban
sinin taban 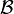 sinin sırasıyla karmaşık matris
sinin sırasıyla karmaşık matris 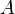 sırasıyla tanımlanıyor,ise
sırasıyla tanımlanıyor,ise 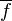 göndermesi
göndermesi 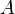 'nın karmaşık eşlenik taban sırasıyla
'nın karmaşık eşlenik taban sırasıyla 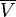 'nın
'nın 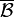 ve
ve 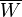 nın
nın 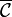 tanımlanıyor.
tanımlanıyor.
Eşlenişiğin yapısı
vektör uzayı 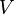 ve
ve 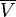 var ve karmaşık sayılar ve bunun için karmaşık vektör uzayı üzerinde aynı boyut olarak izomorfiktir. Bununla birlikte,
var ve karmaşık sayılar ve bunun için karmaşık vektör uzayı üzerinde aynı boyut olarak izomorfiktir. Bununla birlikte,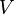 dan
dan 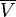 ya burada doğal izomorfizm yoktur. (
ya burada doğal izomorfizm yoktur. (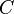 göndermesi bir izomorfizm değildir, dolayısıyla antilineerdir.)
göndermesi bir izomorfizm değildir, dolayısıyla antilineerdir.)
çift eşlenik 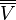 ,
,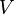 ya doğal izomorfiktir,
ya doğal izomorfiktir, 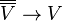 ile izomorfizm ile tanımlanır
ile izomorfizm ile tanımlanır
Genellikle 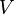 'nın çift eşlenik basit
'nın çift eşlenik basit 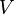 özdeşi iledir.
özdeşi iledir.
Ayrıca bakınız
- Doğrusal karmaşık yapı
Kaynakça
- Budinich, P. and Trautman, A. The Spinorial Chessboard. Spinger-Verlag, 1988. ISBN 0-387-19078-3. (complex conjugate vector spaces are discussed in section 3.3, pag. 26).