Kelebek önsavı

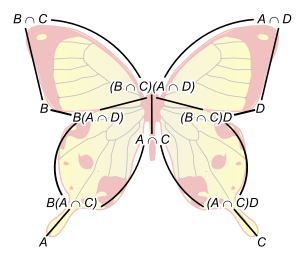
Zassenhaus Hasse diagramı "kelebek" önsavı - daha küçük altgrupları diyagramın üst kısmına doğrudur

matematikte,Kelebek önsavı veya Zassenhaus önsavı, Hans Zassenhaus adına ithaf edilir,bir grubunun altgrupların kafesinin veya bir modülün altmodullerin kafesinin, veya daha genel herhangi moduler kafes için teknik bir sonuçtur.^[1]

Önsav: Varsayım ${\displaystyle (G,\Omega )}$ bir grup ile operatorlerinin ve ${\displaystyle A}$ ve ${\displaystyle C}$altgruplarıdır. Varsayım

${\displaystyle B\triangleleft A}$ ve ${\displaystyle D\triangleleft C}$

kararlı altgruplarıdır. Öyleyse,

${\displaystyle (A\cap C)B/(A\cap D)B}$ ifadesi ${\displaystyle (A\cap C)D/(B\cap C)D.}$ ya eşyapıdır

Schreier arıtma teoremi'nin verilen sorunsuz kanıtını Zassenhaus önsavının özelliği sağlar.İlgili çeşitli grupların çizilen Hasse diagramına çalışırken 'kelebek' belirginleşir.

Notlar

1. See Pierce, p. 27, exercise 1.

Kaynaklar

• Pierce, R. S. (1982), Associative algebras, Springer, ss. 27, ISBN 0-387-90693-2 .
• Goodearl, K. R.; Warfield, Robert B. (1989), An introduction to noncommutative noetherian rings, Cambridge University Press, ss. 51, 62, ISBN 978-0-521-36925-1 .
• Lang, Serge, Algebra, Graduate Texts in Mathematics (Revised 3rd bas.), Springer-Verlag, ss. 20–21, ISBN 978-0-387-95385-4 .
• Carl Clifton Faith, Nguyen Viet Dung, Barbara Osofsky (2009) Rings, Modules and Representations. p. 6. AMS Bookstore, ISBN 0-8218-4370-2
• Hans Zassenhaus (1934) "Zum Satz von Jordan-Hölder-Schreier", Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 10:106–8.
• Hans Zassenhaus (1958) Theory of Groups, second English edition, Lemma on Four Elements, p 74, Chelsea Publishing.

Dış bağlantılar

• Zassenhaus Lemma and proof at http://www.artofproblemsolving.com/Wiki/index.php/Zassenhaus%27s_Lemma